5年生『 合同な図形 』
基本から発展までいくぞ!
Web算数問題集
5年生におすすめ、合同な図形を完全マスターする問題集
2つの図形がぴったり・きちんと・バッチリ・バシッと・きちっと、、、重なるとき、
この2つの図形は合同である!
といいます。
図形が合同か、合同ではないのか・・ジャッジするのは君だ。 よしっ やろう
もくじ
ぴったり合同
次の2つの三角形は形や大きさが同じです。下の問いに答えよう。
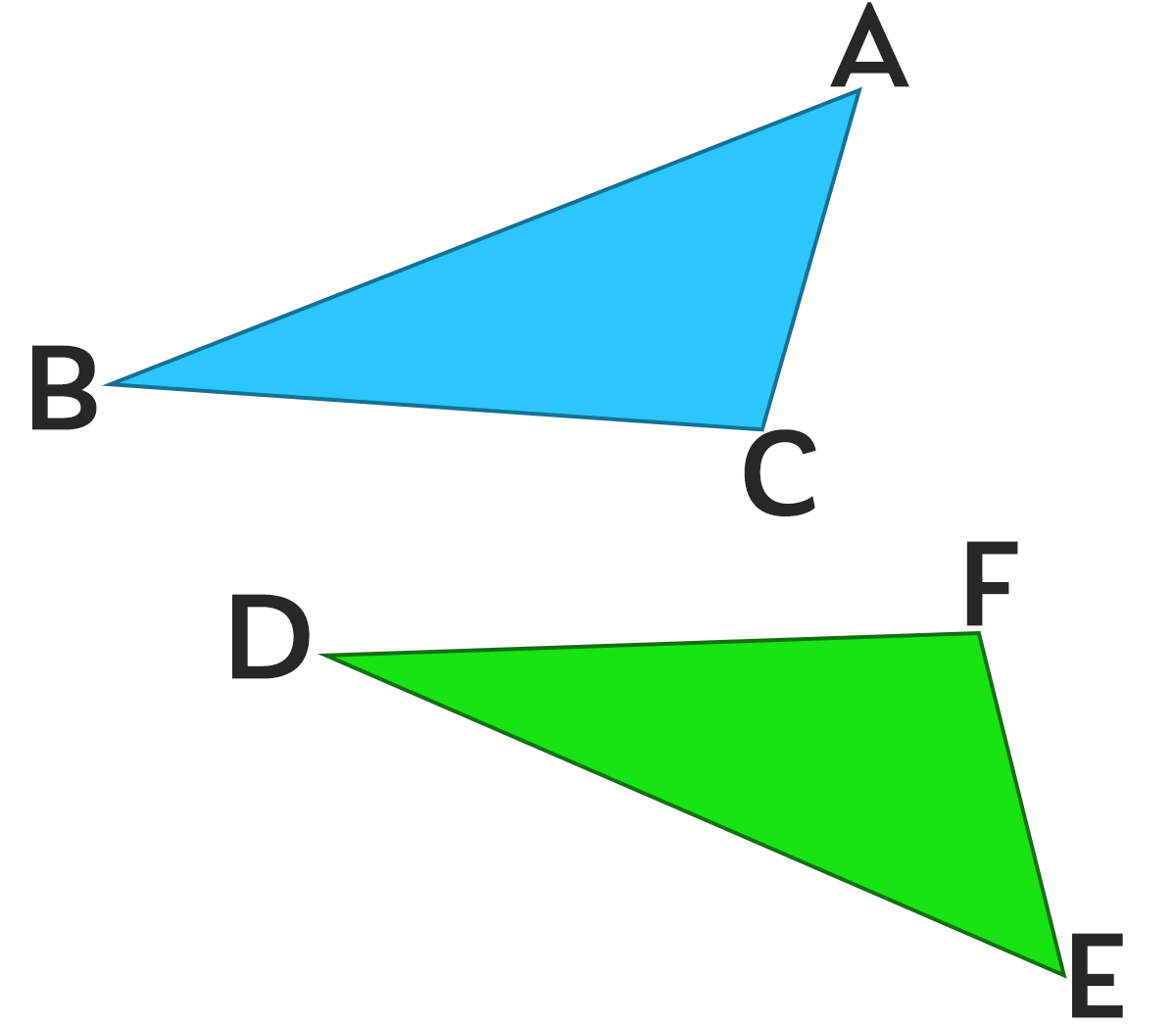
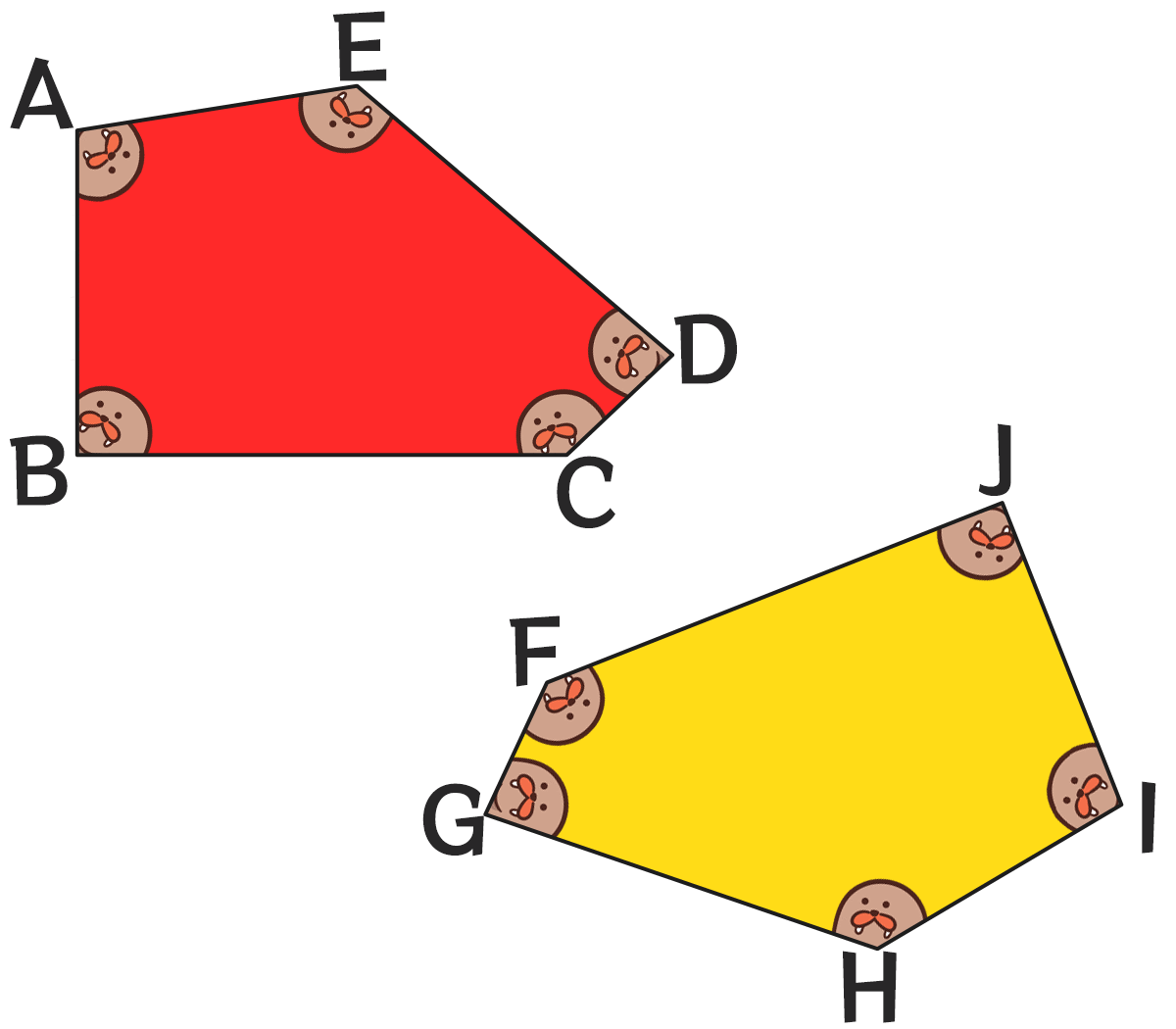
対応する頂点は、
対応する辺は、
合同な2つの五角形があります。角から生物がのぞいているが気にせず下の問いに答えよう。
三角形の合同条件

2つの三角形が合同かどうか見破る方法が3つある。
3つの条件のうち、ひとつでも当てはまれば、その三角形たちは合同だ。
その3つの条件を「三角形の合同条件」といいます!

三角形の合同条件を紹介しまーす
「 三角形の合同条件 」
3組の辺が それぞれ等しい。
2組の辺と その間の角が それぞれ等しい。
1組の辺と その両端の角が それぞれ等しい。
図と一緒に見たほうが分かりやすいかも!
ひとつずつ見ていこう。別にむずかしくないよ~
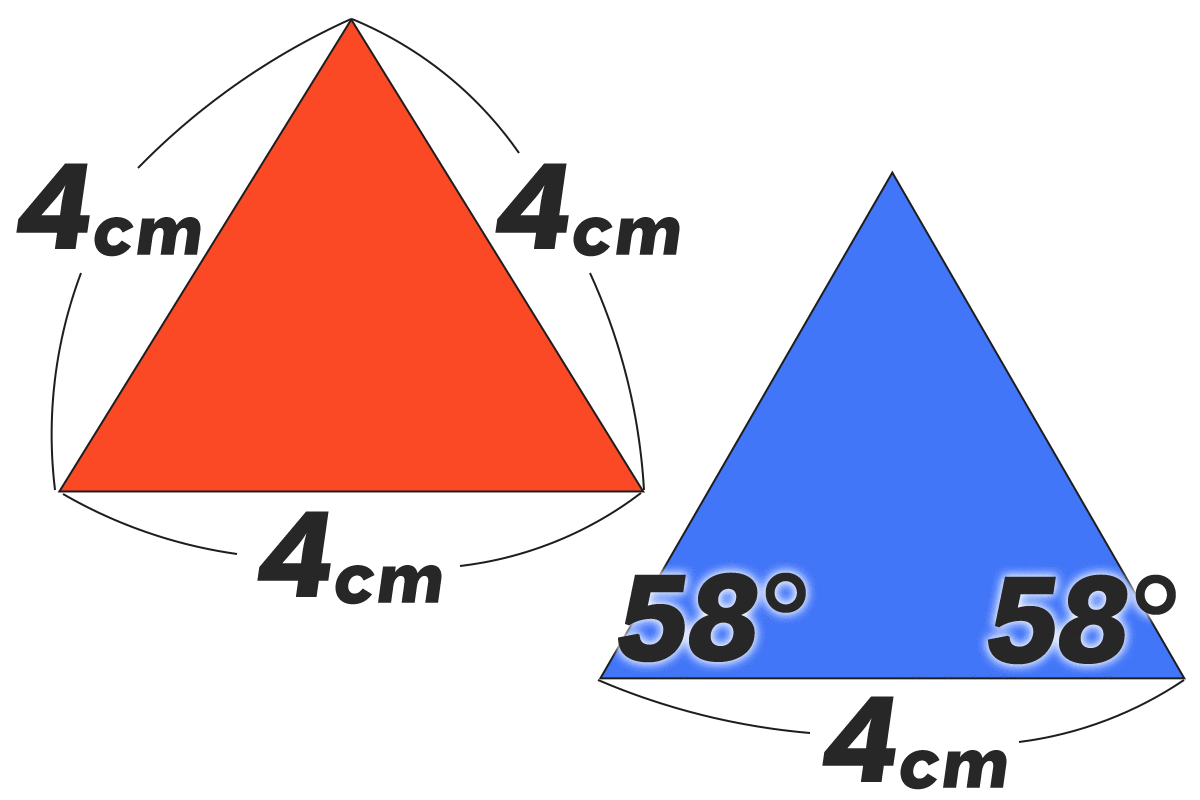
その前に、、この2つの三角形って合同だと思う?


知らんがな
なんか手がかりちょうだい
ではいきます。
3組の辺が それぞれ等しい
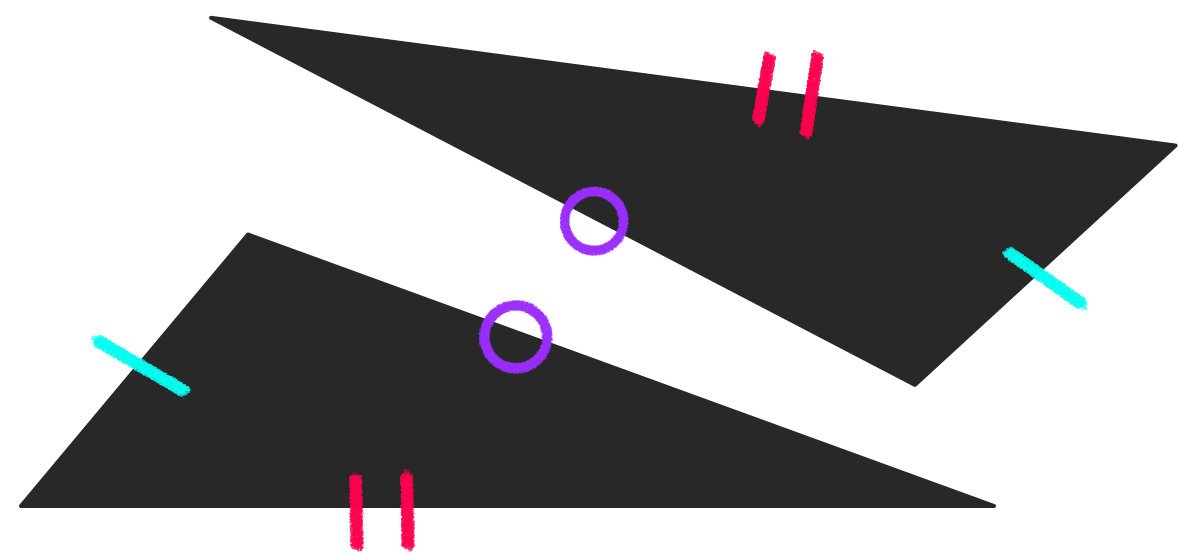
向きはちがうけど 辺の長さは3組とも同じ。

3辺がそれぞれ同じ長さなら、この2つの三角形は合同です!
3辺が同じ長さなら、角度も同じだし
3組の辺がそれぞれ等しければ、わざわざ角度まで測らなくても合同といってOK!
2組の辺と その間の角が それぞれ等しい
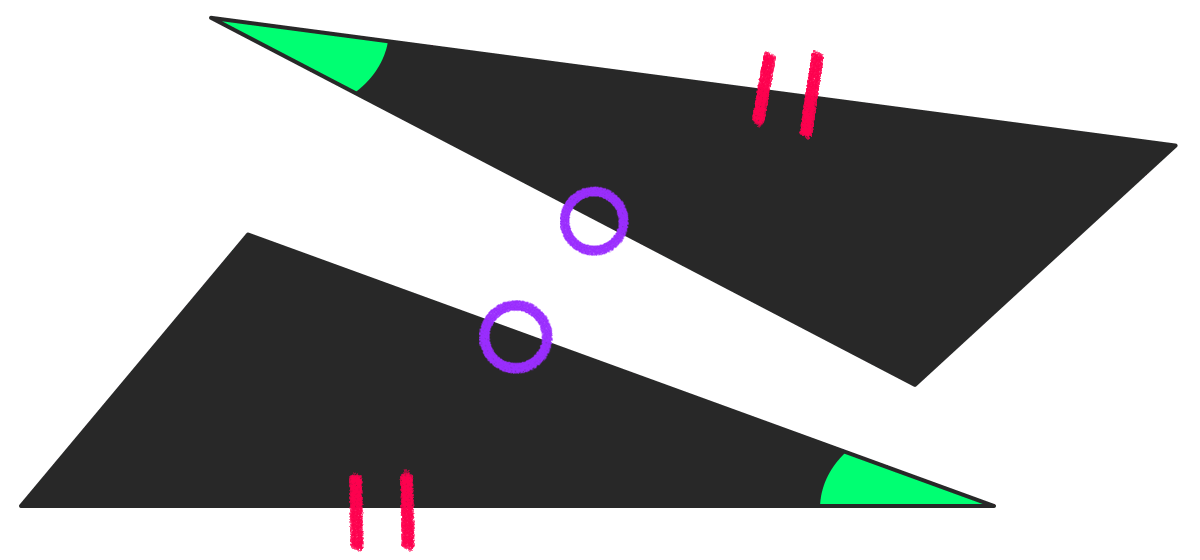
2つの辺の長さと その間の角が同じ。

この2つの三角形は合同です!
2組の辺とその間の角がそれぞれ等しければ、残りの辺と角も等しいから 合同といってOK!
1組の辺と その両端の角が それぞれ等しい
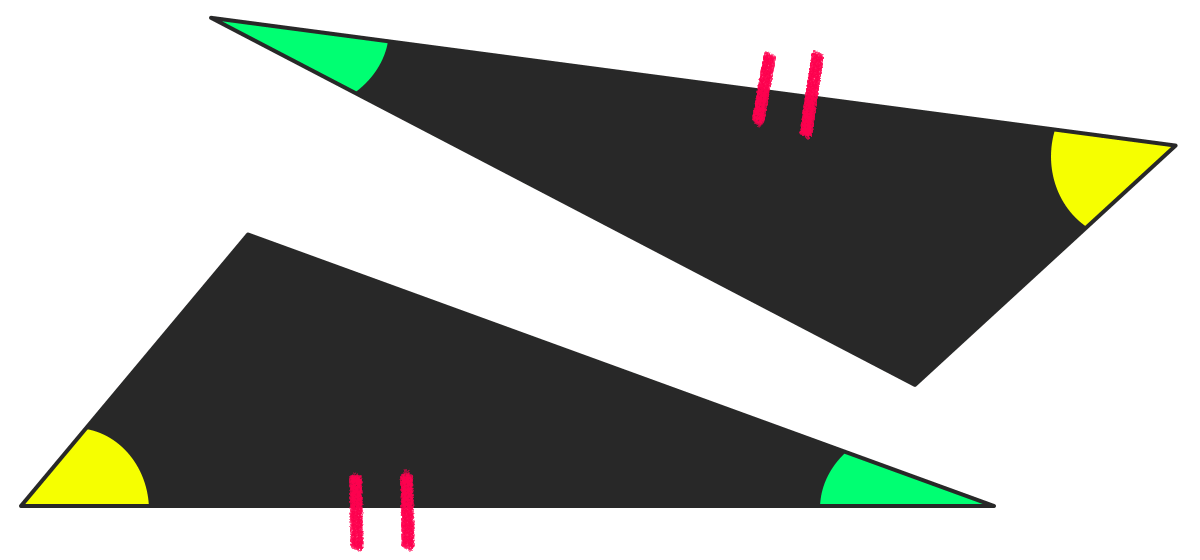
1辺と その両端の角が同じ。

この2つの三角形は合同です!
1組の辺とその両端の角がそれぞれ等しければ、残りの辺と角も等しいから 合同といってOK!
三角形の合同条件のうち、どれか1つに当てはまれば 自信を持って 「合同~!」
辺と角をぜ~んぶ調べなくても、合同か・合同ではないか、ジャッジできる
三角形の合同条件をすべて答えましょう。
ジャッジメント・ナイト
合同か・合同じゃないか
見極めろ!5問
2つの図形が合同か・合同じゃないか答えてくれ。そして、なぜそう思ったか理由もたのむぞ。
- (1)
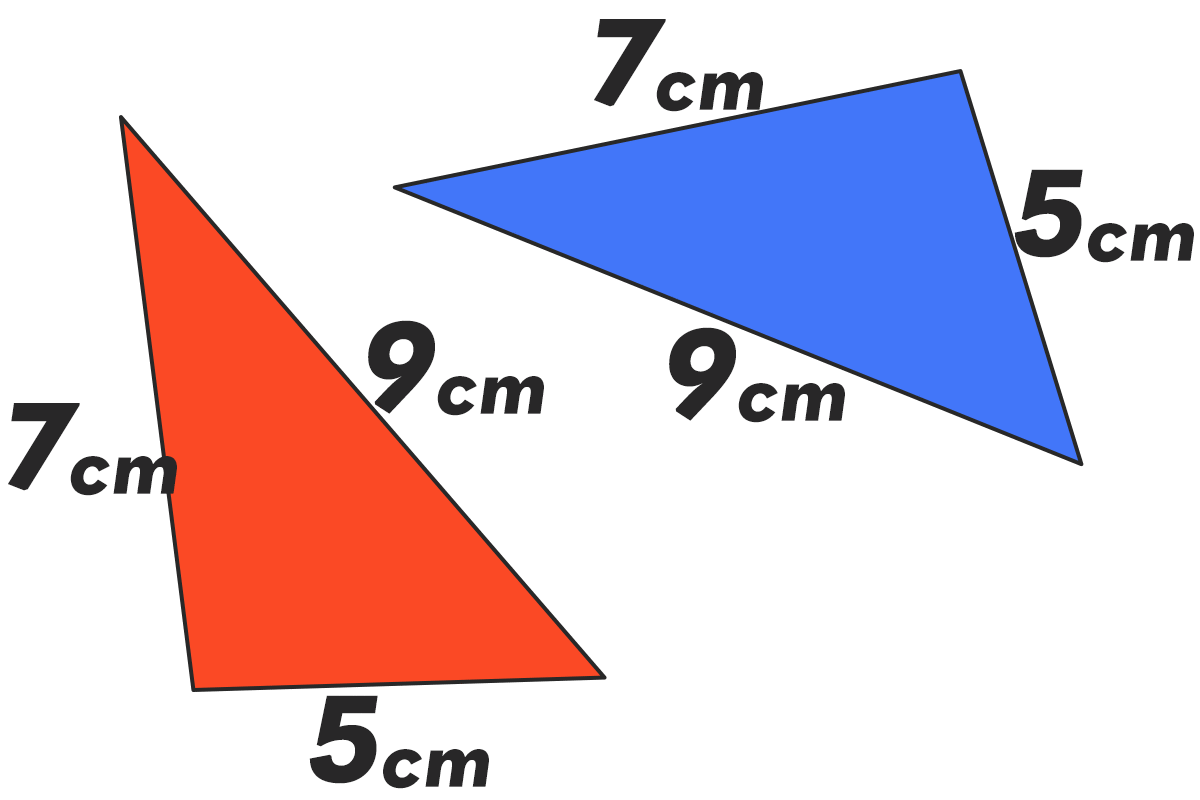
- (2)
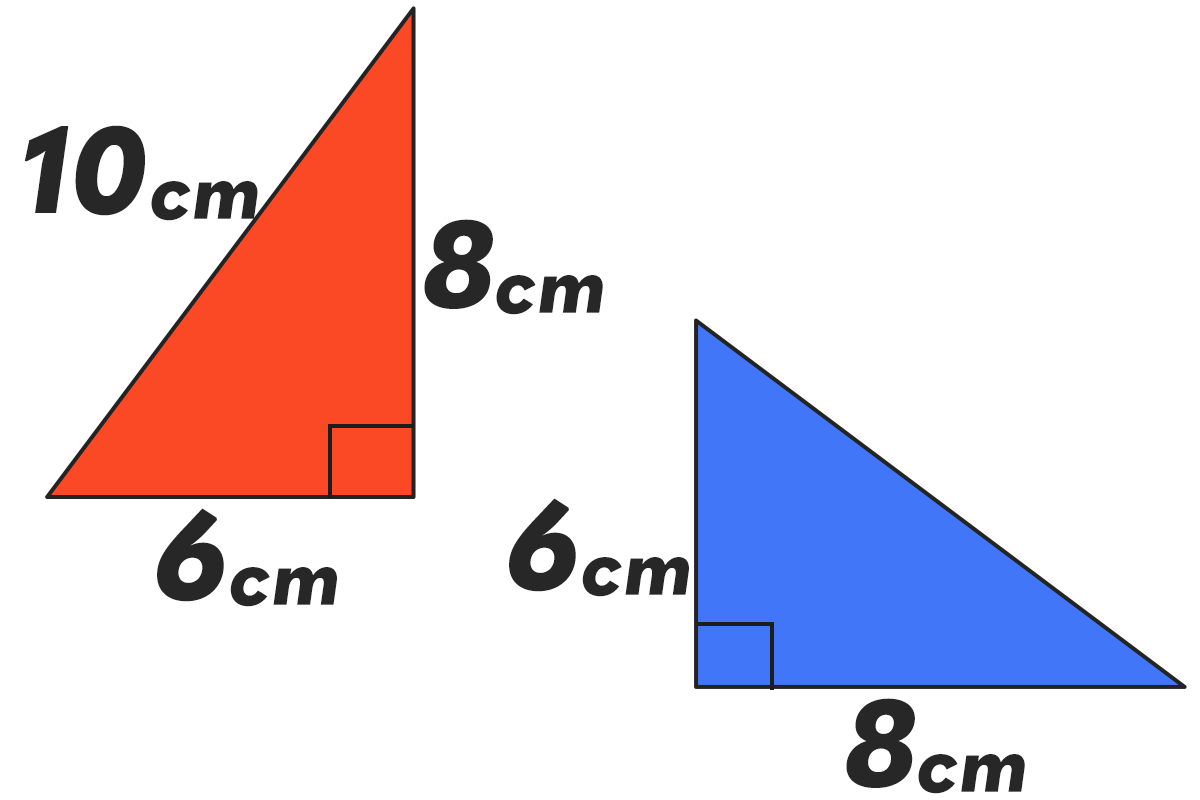
- (3)
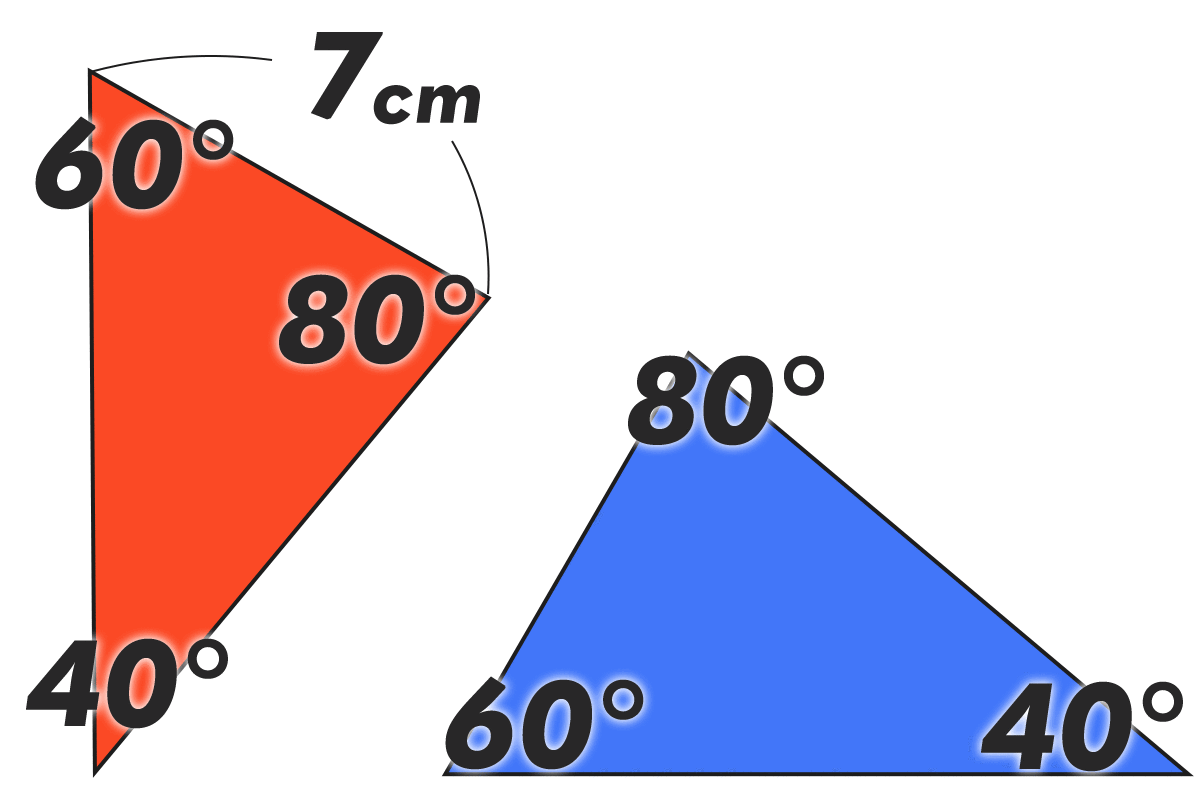
- (4)
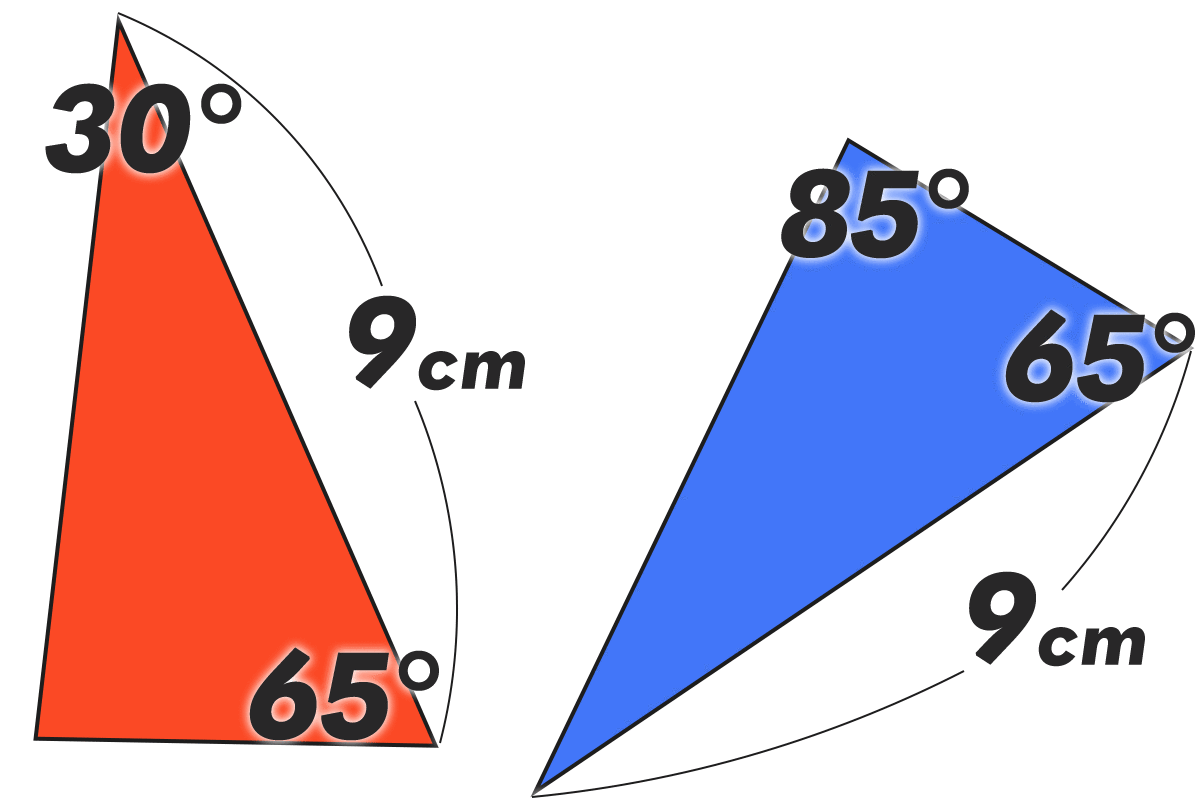
- (5)
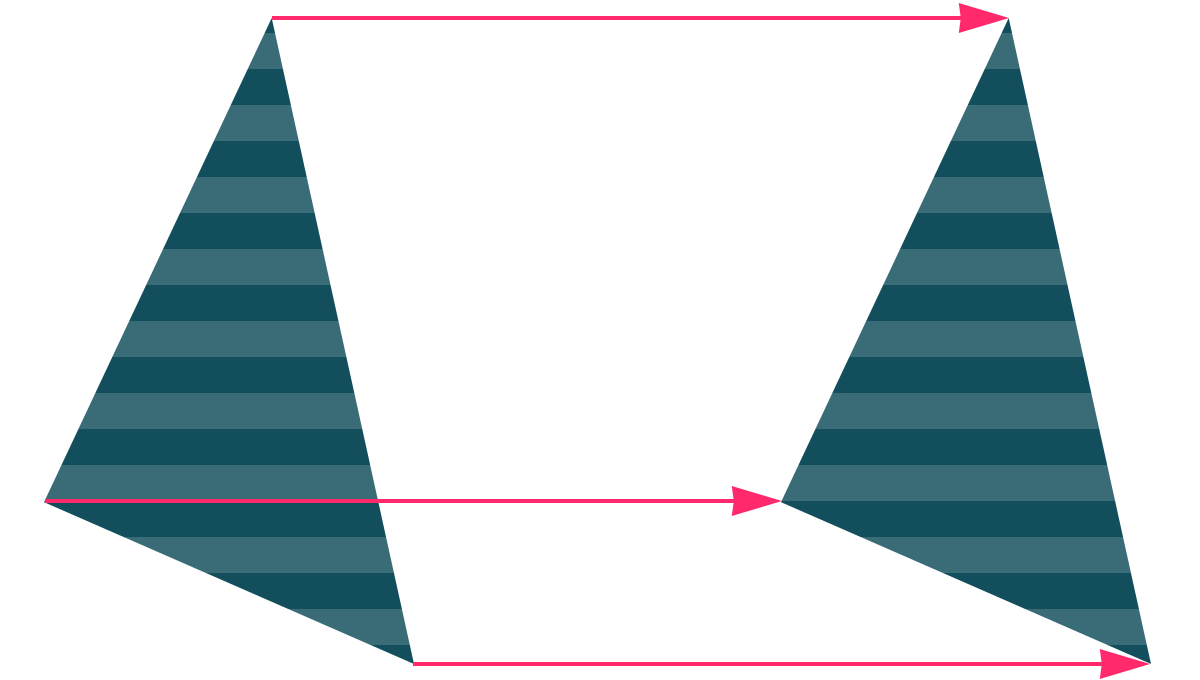
スーッと動かせ平行移動!

おっ!平行移動
上の図のように、平面図形を 一定の方向に、一定のきょりだけ移すことを平行移動 といいます。

横に移すだけじゃなく、
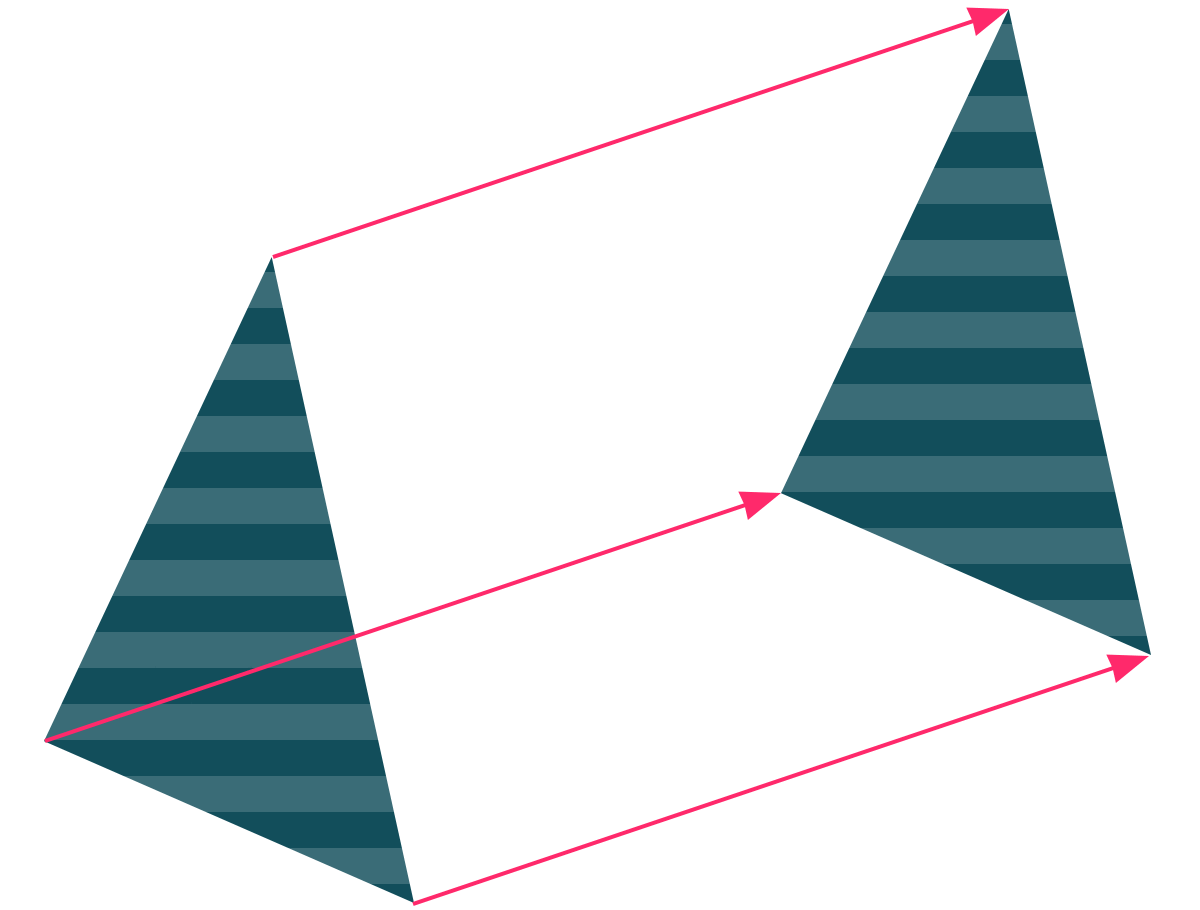
こんなふうに、ななめ上でも、下でも、一定の方向に移すことを平行移動といいます!
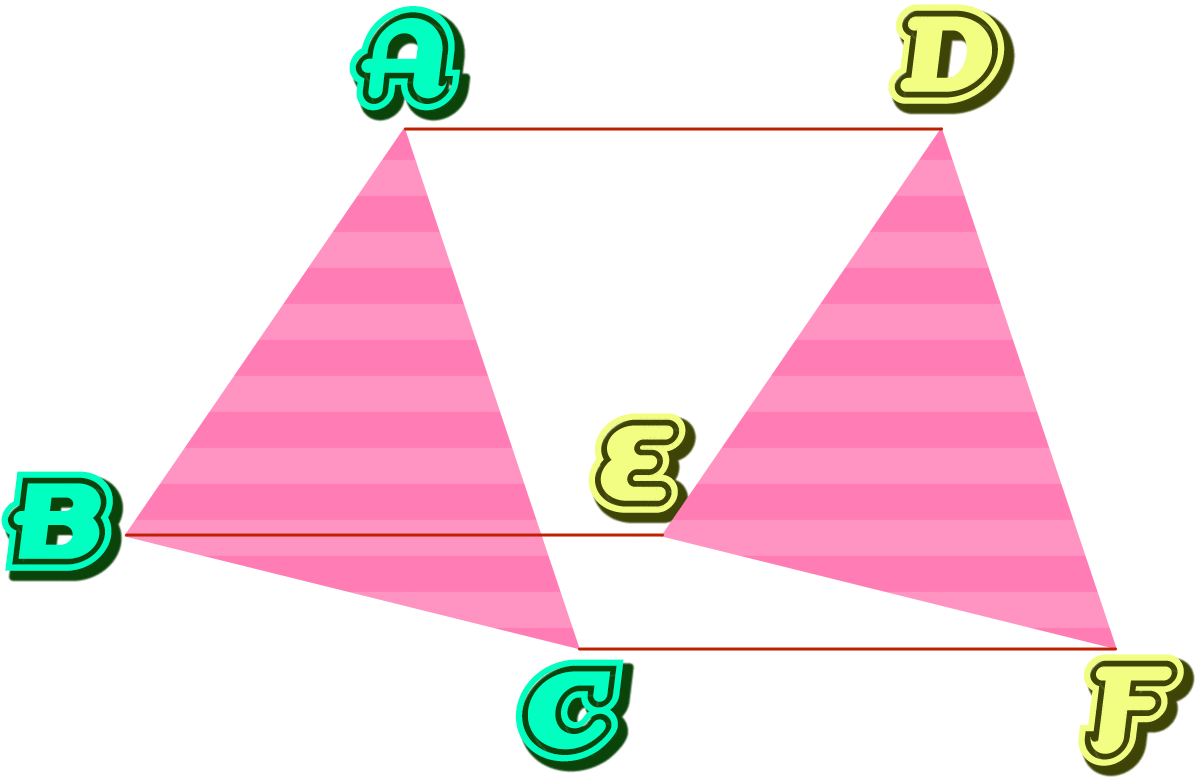
三角形ABCを 右に7cmずらして、三角形DEFに移しました。次の問いに答えたくなったら答えましょ。
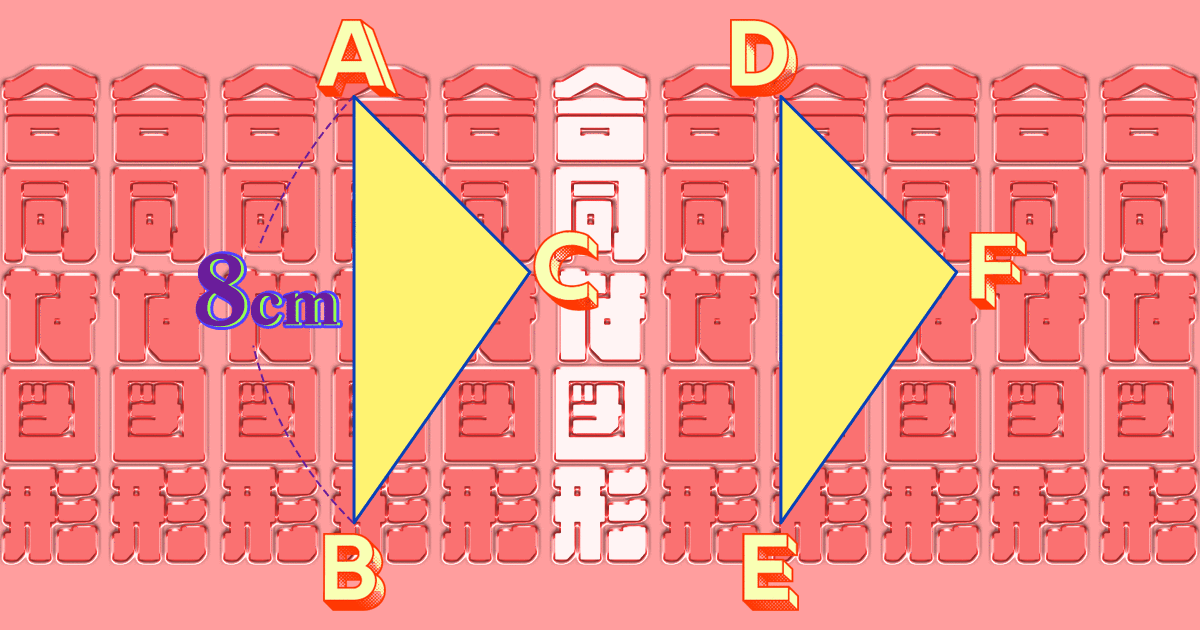
三角形ABCを 右に8cmずらして、三角形DEFに移し、頂点BとEを直線で結びました。次の問いに答えましょう。
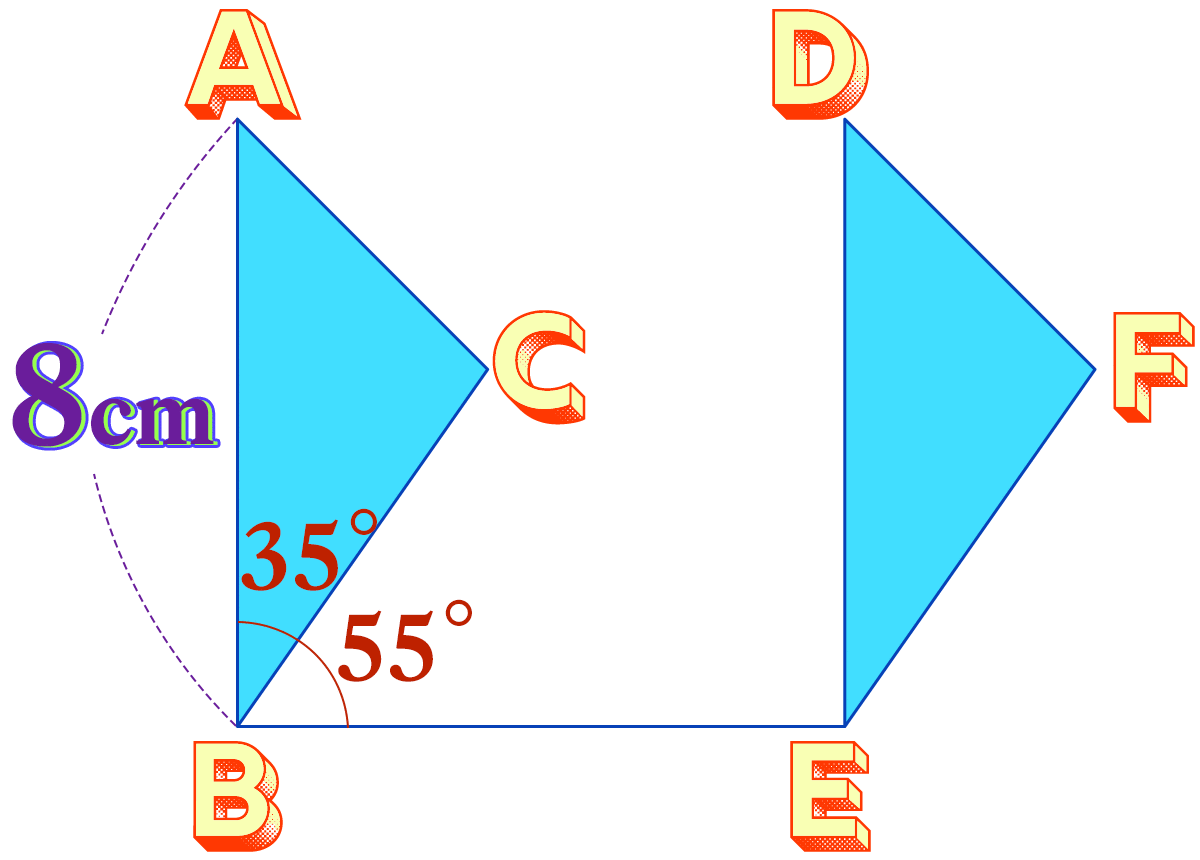
辺DEの長さは何cmですか。
頂点CとFを直線で結ぶとできる 四角形CBEFの名前は何でしょう。
四角形CBEFの 角Eの大きさは何度ですか。
頂点DとBを直線で結ぶとできる 三角形DBEの名前は何でしょう。
図で見る答え
- 8cm
- 平行四辺形
- 125°
- 直角二等辺三角形
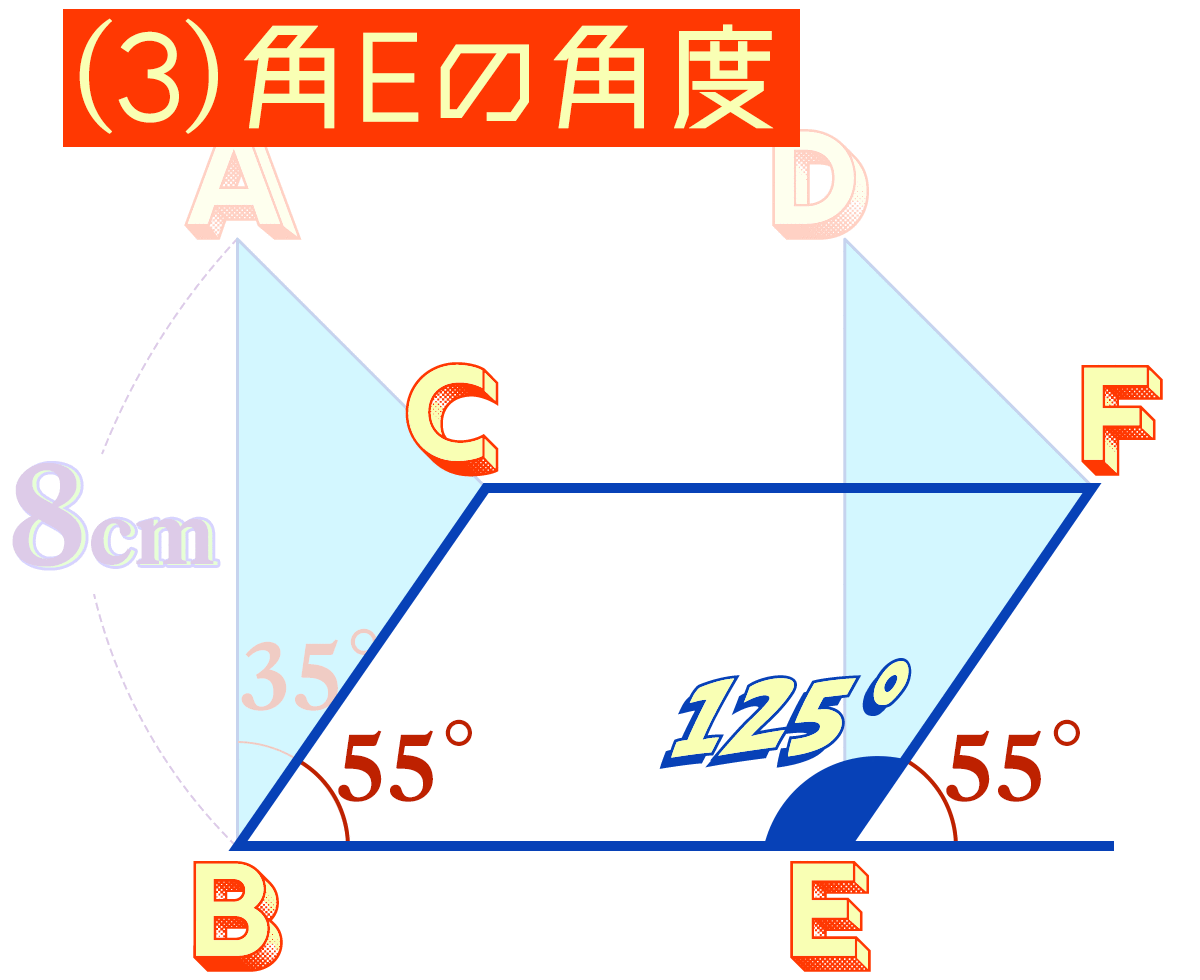
角Eの外側も55°だから、180-55=125
他にも、
「平行四辺形の向かい合う角は等しい」と「四角形の内角の和は360°」を使っても出せる~
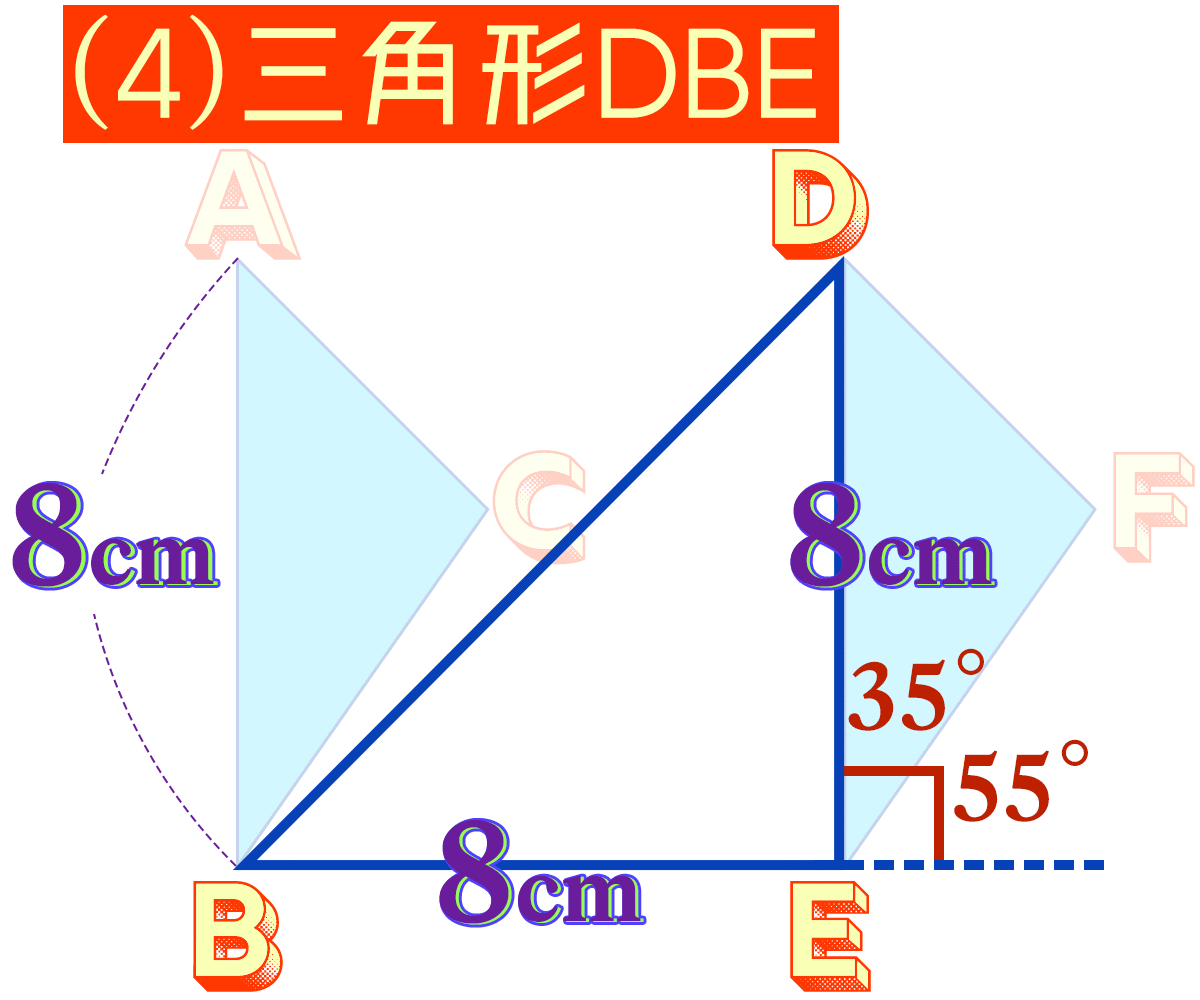
8cmずらしてるから 辺BEは8cm
角Eの外側の角度は、
35+55=90
だから、角Eも90°ちょっかーーく
というわけで 直角二等辺三角形です
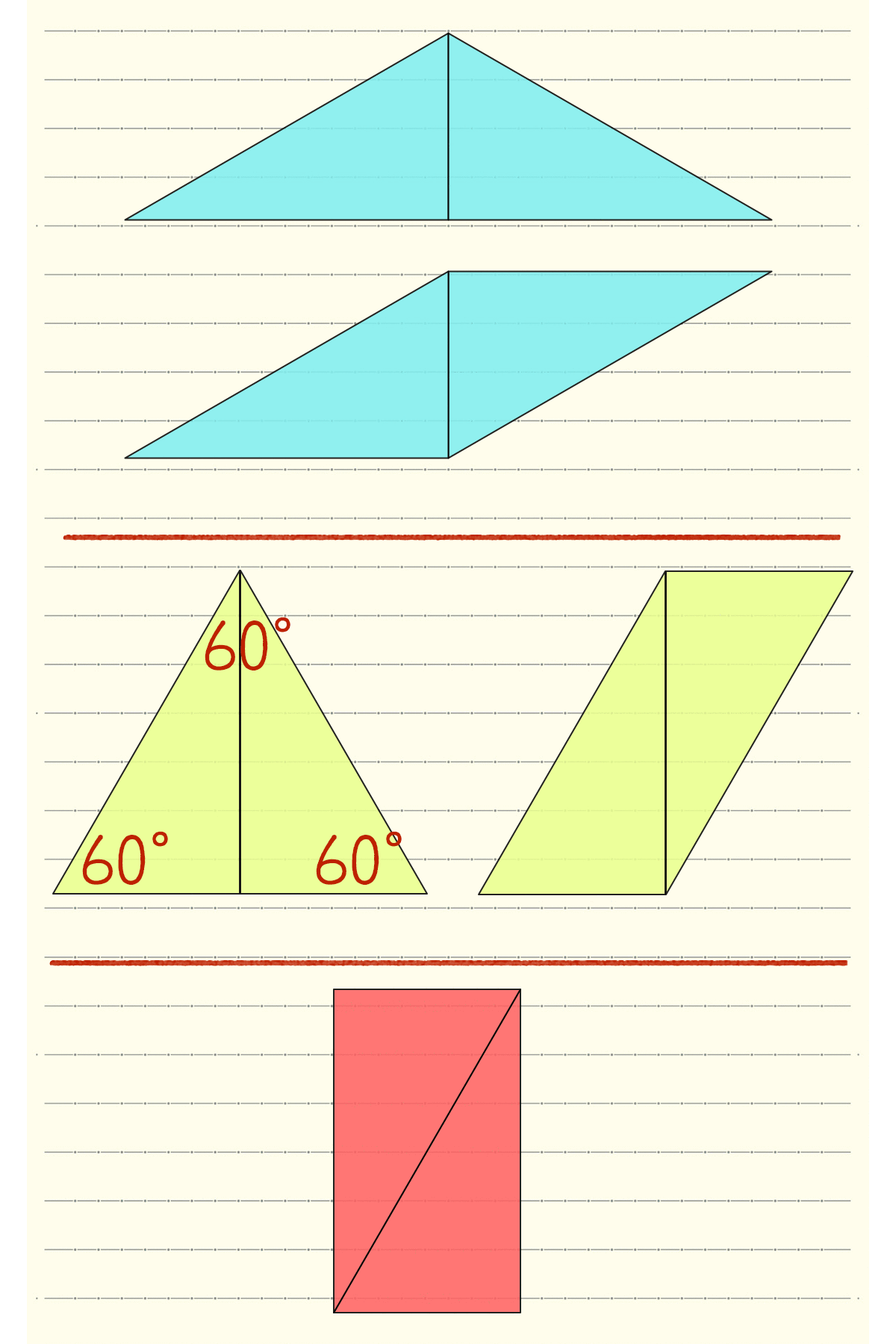
角度が30°、60°、90°の2つの合同な直角三角形があります。対応する辺をぴったり合わせるとどんな図形ができますか。下の7つからすべて選びましょう!
「 台形、平行四辺形、ひし形、長方形、正方形、二等辺三角形、正三角形 」
1番短い辺を合わせたとき
2番目に長い辺を合わせたとき
斜辺を合わせたとき
答え合わせ
- 平行四辺形、二等辺三角形
- 平行四辺形、正三角形
- 長方形
辺の長さとか 角度を考えると答えが出るよ。
書いてみるのもおすすめ