分数の割り算はなぜひっくり返して掛けるのか?理由を見たら納得!

分数の割り算は、なぜ割る数の逆数を掛けると答えが出るのか。図解付きでわかりやすく解説します!
分数の割り算のやり方が疑問だった人もこれで納得。
この疑問について、まず、みんなが知りたそうな答えを先に書きます。
だけど、このページで言いたいことは全然ちがう!だから最後まで見てね~

マジメに 解りやすく 楽しくいくぜ

6年生【分数の割り算 問題 244問!】
分数の割り算の計算問題たっぷりです。やってみてね
分数の割り算はなぜ割る数の逆数を掛けるのか
(例) $ \dfrac{2}{5} \div \dfrac{3}{4} = $
下の図を見てみよう
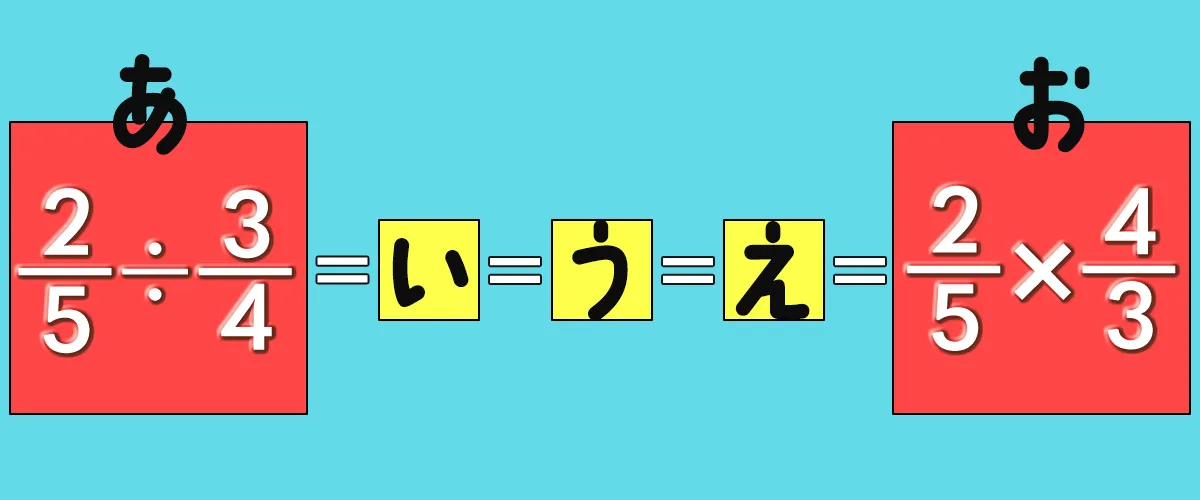
いつも分数の割り算は、(お)で計算してる。
割る数を逆数にして かけ算ね。

その間の計算をすっ飛ばしてるから、「なんで逆数で掛ける??」ってことになる。
(い)(う)(え)を順番にやってみます。
まずは、(い)!
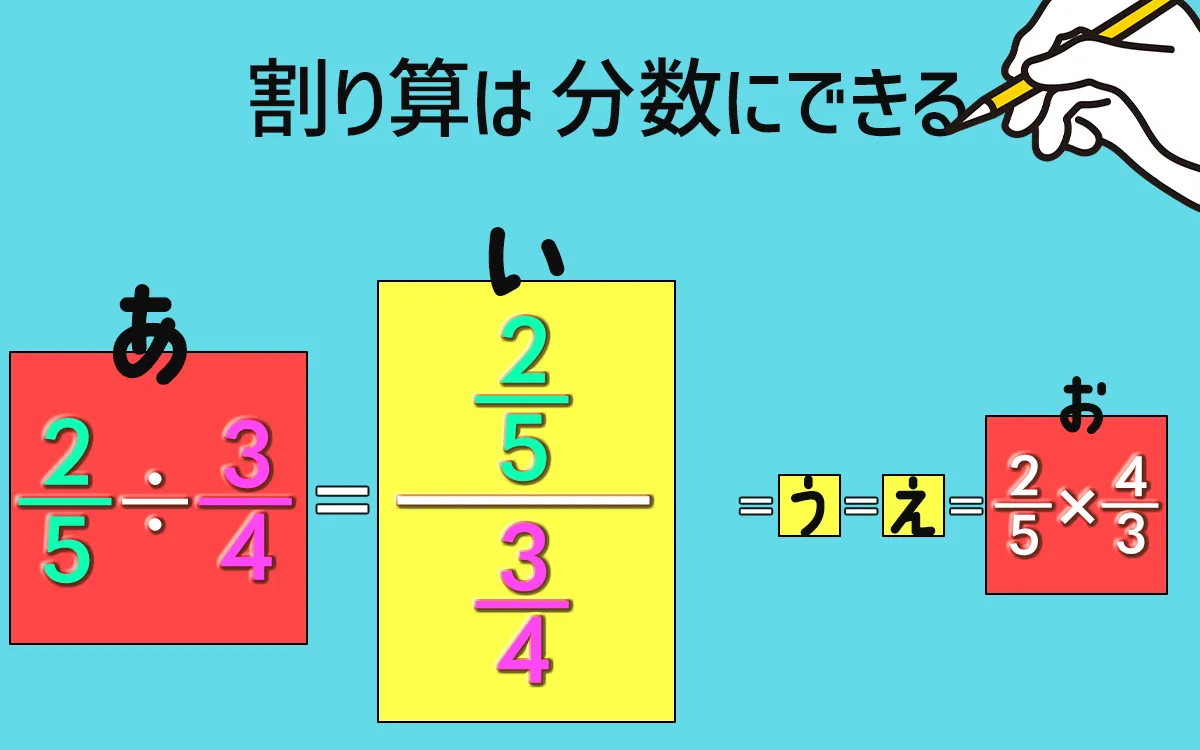
割り算は分数の形になるよね。
(例) 2÷3=
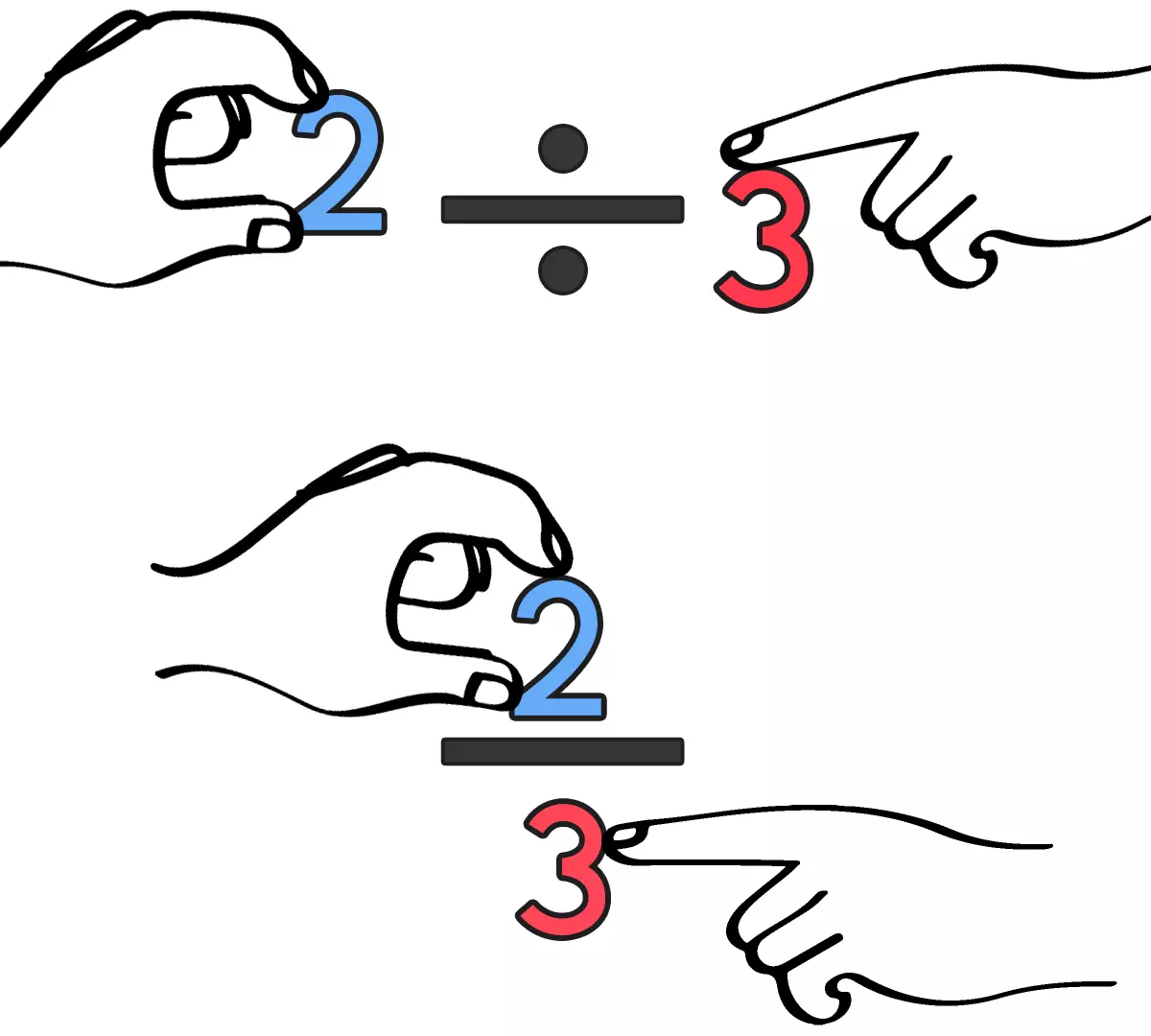
割る数が分母で、割られる数が分子
だから、
$ \dfrac{2}{5} \div \dfrac{3}{4} = \dfrac{\cfrac{2}{5}}{\cfrac{3}{4}} $

$ \dfrac{2}{3} $は分かるけど、$ \dfrac{\cfrac{2}{5}}{\cfrac{3}{4}} $
4分の3 分の 5分の2 って何だよ?
ぶんぶんぶんっておかしいだろ!って?
これは、繁分数と呼ばれる分数
分母が分数、分子が分数、分母も分子も分数。こういう分数を繁分数といいます!
では、次いきます。
つぎは、(う)!
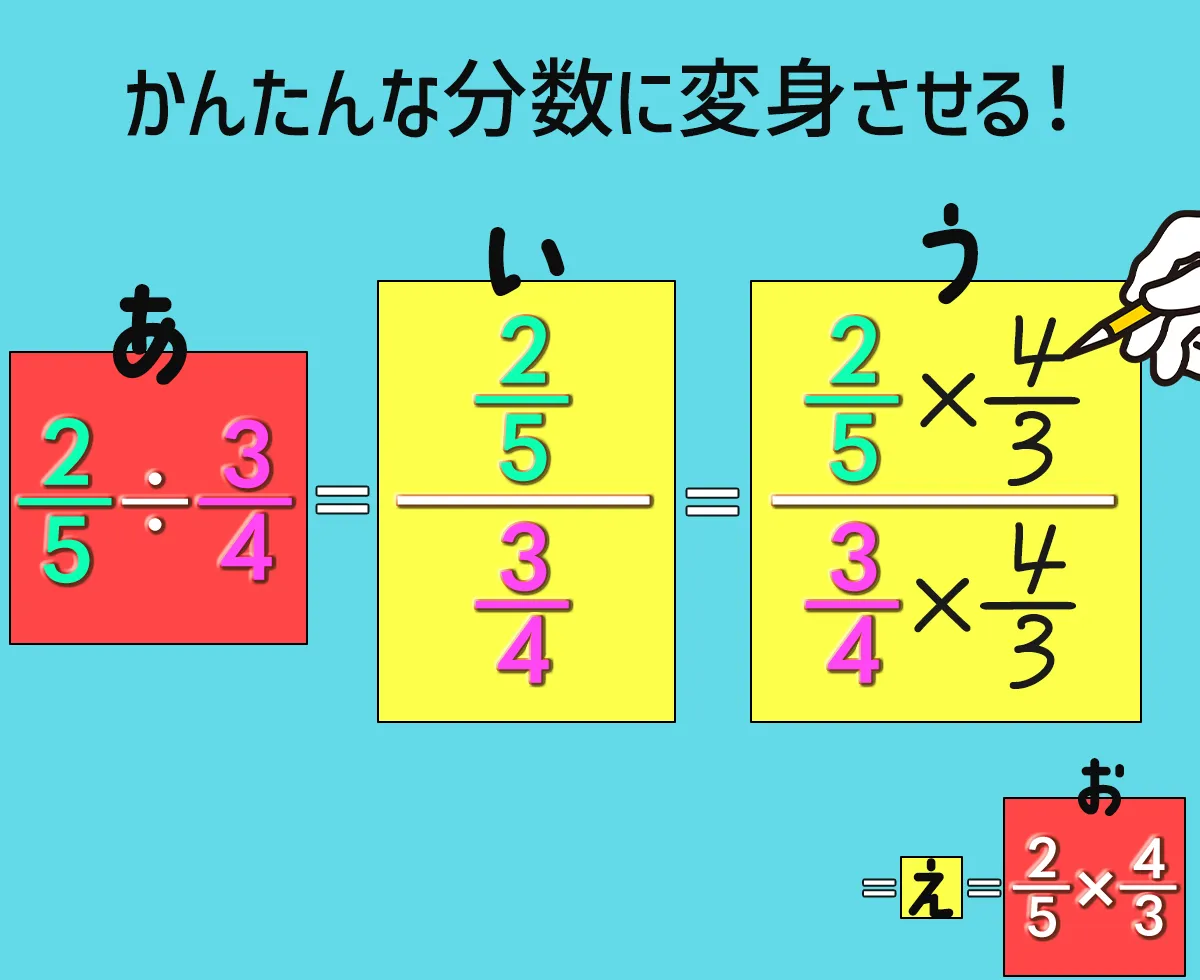
(い)の繁分数がややこしいので、かんたんな分数に変身させたい。
かんたんな分数と言えば、

分母が1
分数は、分母と分子に同じ数を掛ければ大きさは変わらない。
分母の$ \dfrac{3}{4} $に 逆数の $ \dfrac{4}{3} $を掛ければ 1になる。
分子にも同じ $ \dfrac{4}{3} $ を掛けてやれば、大きさは変えずにシンプルな分数に変身させることができる!!
つぎは、(え)
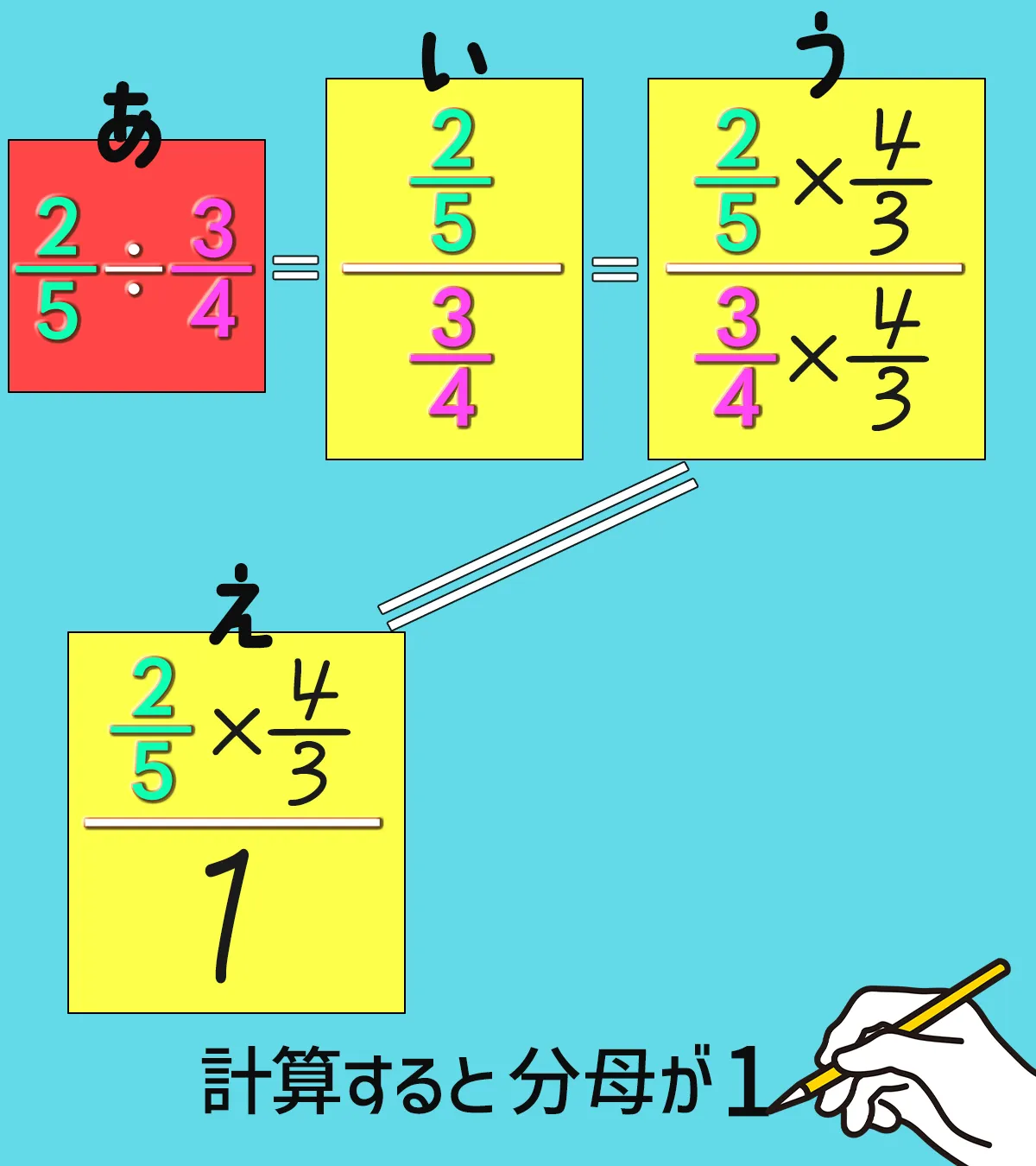
(う)を計算すると、分母が1です。
では最後を見てみましょう
最後(お)!
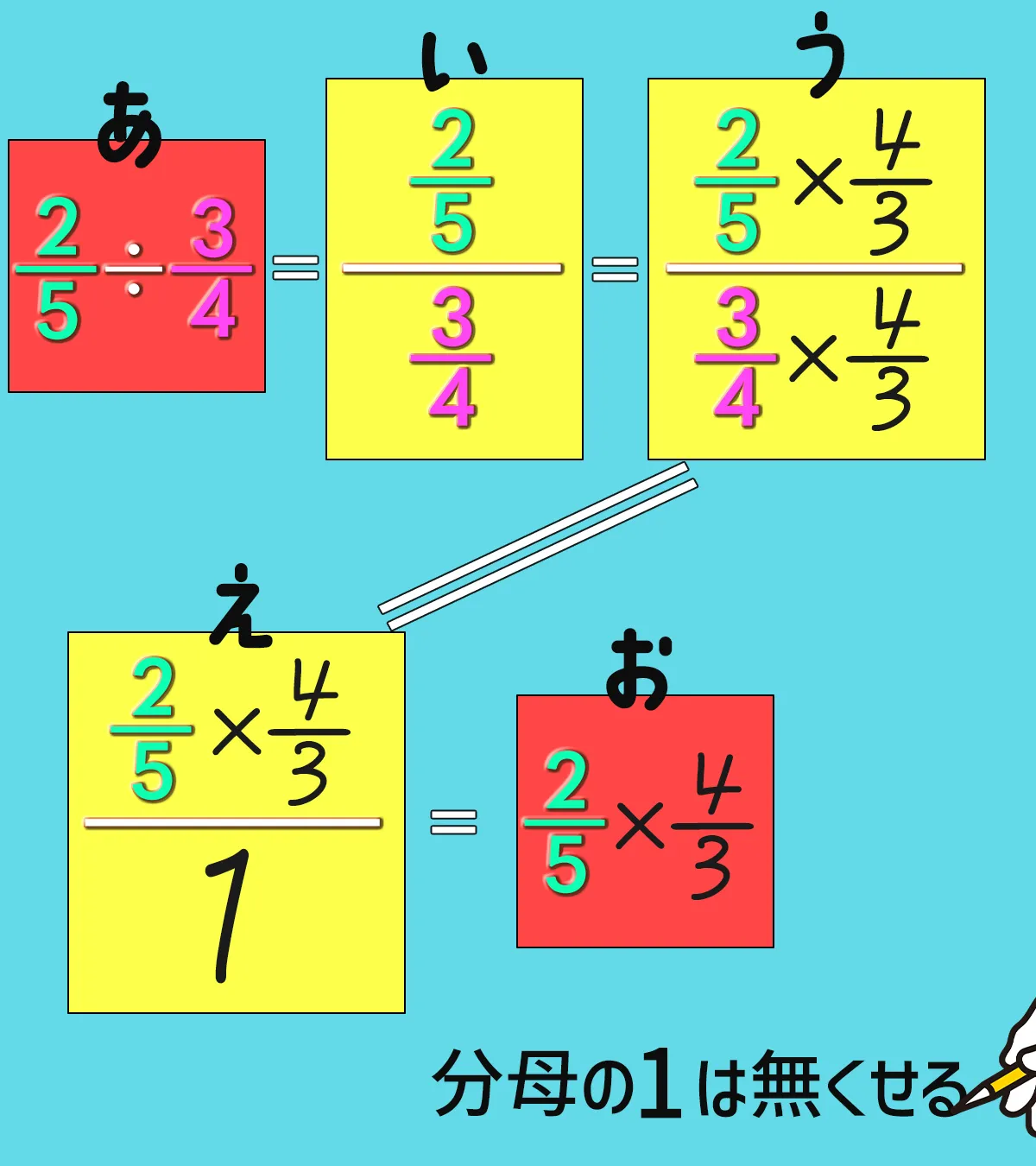
分母の1を無くして、$ \dfrac{2}{5} \times \dfrac{4}{3} $
いつもの分数の割り算のやり方になった!
割る数を逆数にして掛けるのは、こういう道のりがあった。

いつもは近道で いきなり(お)で計算してたのね

ちょっとまって
そもそも割り算は割る数を逆数にしてかけ算すれば答え出るから!
~ここからが本番~
分数の割り算はなぜひっくり返して掛けるのか?っていうけど、
整数の割り算だってそうやってる時あるよ。
割り算は、割る数を逆数にして掛けることで計算できるものなんだ!
(例) 2÷3=
割る数を逆数にしてかけ算ね

3を逆数にして掛ける
$ 2 \div 3 = 2 \times \dfrac{1}{3} = \dfrac{2}{3} $
答えは、$ \dfrac{2}{3} $
割りきれる割り算でもやってみる
(例) 10÷2=
$ 10 \div 2 = 10 \times \dfrac{1}{2} = \dfrac{10}{2} = 5 $
答えは、5! できた~

$ \dfrac{10}{2} $で 結局 10÷2をやってるな
ただ遠回りしてるだけだ
割り算は、割る数を逆数にすることでかけ算で答えを出すことができる。だけど、分数じゃないとただの遠回りだから わざわざやらない。
ひっくり返して掛けることで答えが出るのは、分数の割り算だけじゃないよ!
って話でした。

つぎで最後、一番やりたかったこと
マジかよ!?分数の割り算も 分母同士・分子同士で割り算すれば計算できる
分数のかけ算は、分母同士、分子同士でかけ算するよね?
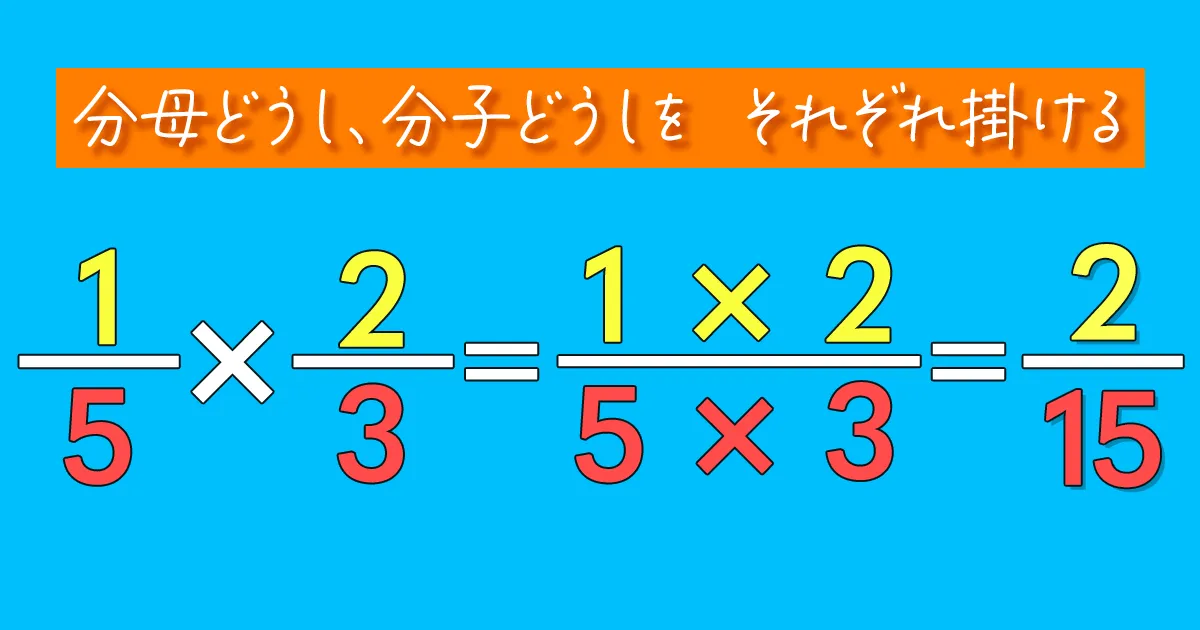
実は!!分数の割り算もこれでイケます。
(例) $ \dfrac{3}{8} \div \dfrac{1}{2} = $
分母どうし・分子どうしで割り算してみる
$ \dfrac{3}{8} \div \dfrac{1}{2} = \dfrac{3 \div 1}{8 \div 2} = \dfrac{3}{4}$
できる!
じゃあなんでこれでやらないの??

面倒くさいんです。
これやってみてよ
$ \dfrac{2}{3} \div \dfrac{7}{13} = $
$ \dfrac{2}{3} \div \dfrac{7}{13} = \dfrac{2 \div 7}{3 \div 13} = \dfrac{0.2857..}{0.2307..} $
割りきれない。$ \dfrac{26}{21} $ にならない!

と思いきや、できる
$ \dfrac{2}{3} $の分母と分子に 91を掛けてから計算するとできる。
$ \dfrac{2 \times 91}{3 \times 91} = \dfrac{182}{273} $
$ \dfrac{2}{3} $ を $ \dfrac{182}{273} $ に変える。
分数は分母と分子に同じ数を掛けても、分数の大きさは変わらないから これはOK!
$ \dfrac{182}{273} \div \dfrac{7}{13} = \dfrac{182 \div 7}{273 \div 13} = \dfrac{26}{21} $
できた!

なんで91を掛けたのかというと
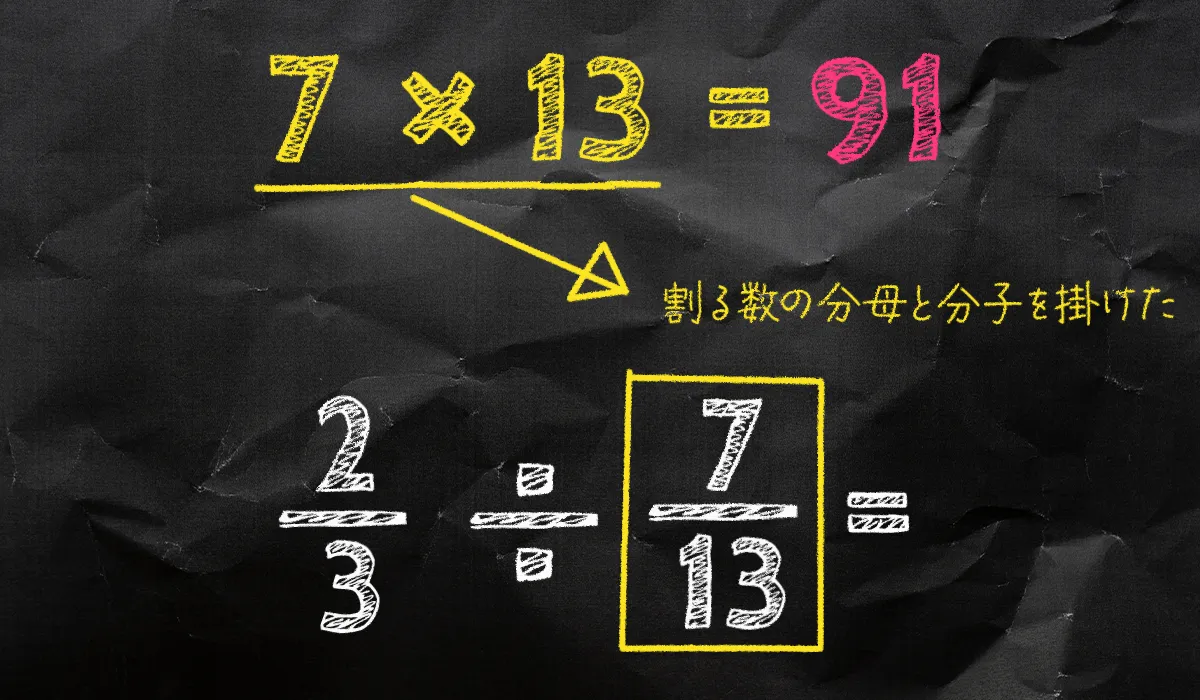
割る数の分母と分子を掛けた数が91
割りきれないときは、こうすると割り切れて答えが出る。
というわけで、分数の割り算も 分数のかけ算みたいに分母同士、分子同士で割り算しても計算できる。
でも、、
できるけど面倒くさい。
「分数の割り算は、割る数を逆数にして掛ける」 これが一番楽ちん

割り算は、割る数を逆数にして掛けることで計算できるものなんだから、楽な方法でやるのが一番いい。
おつかれ