【小学3年生の図形】WEB問題集で三角形と角・角度をやるぞ

3年生におすすめの図形の問題がいっぱい。三角形と角・角度をやります!
3年生で習う三角形と言えば、二等辺三角形 と 正三角形 です。

読み方
二等辺三角形とか言われると むずかしそうに聞こえるけど、ぜんっぜん そんなことはない。

楽勝
もくじ
- 三角形と角・角度
辺・ちょう点・角
辺 と ちょう点 は2年生でやってるね。
3年生では 角が 仲間入り!
そして、角の大きさのことを角度 っていうのも ついでにおぼえちまってください。

三角形には 辺・ちょう点・角がある。角の大きさのことを角度という。
三角形のここはなに? (ア)~(ウ)の名前は何でしょう。
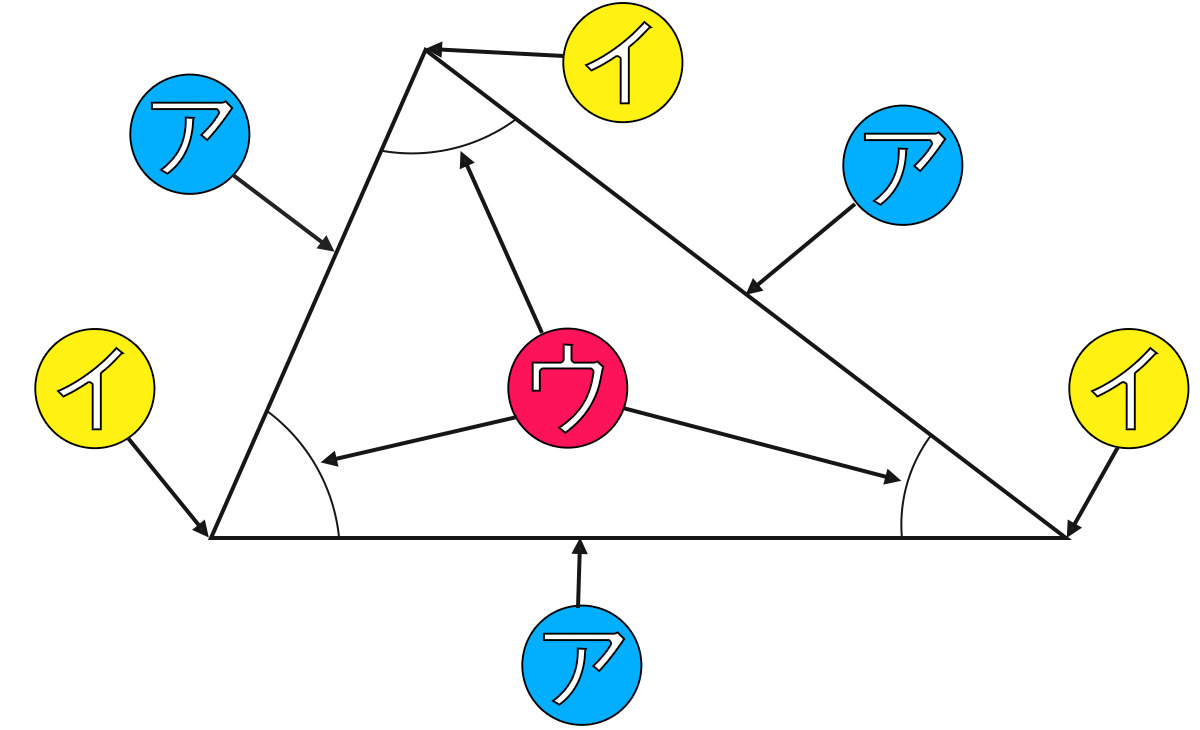
答えは□をクリック
(ウ)の大きさのことを何というでしょう。
角と角度
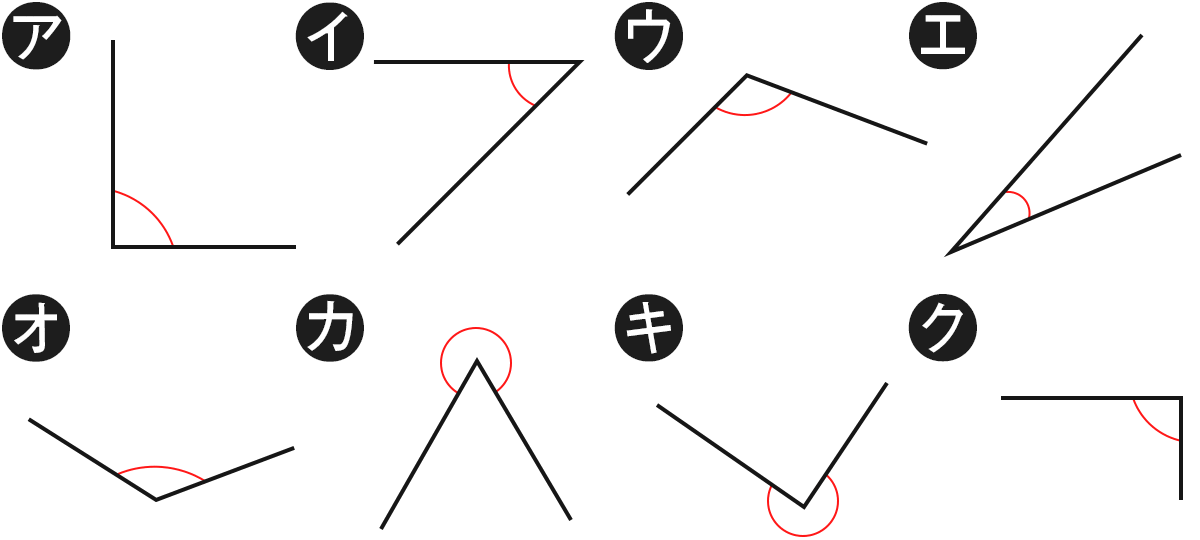
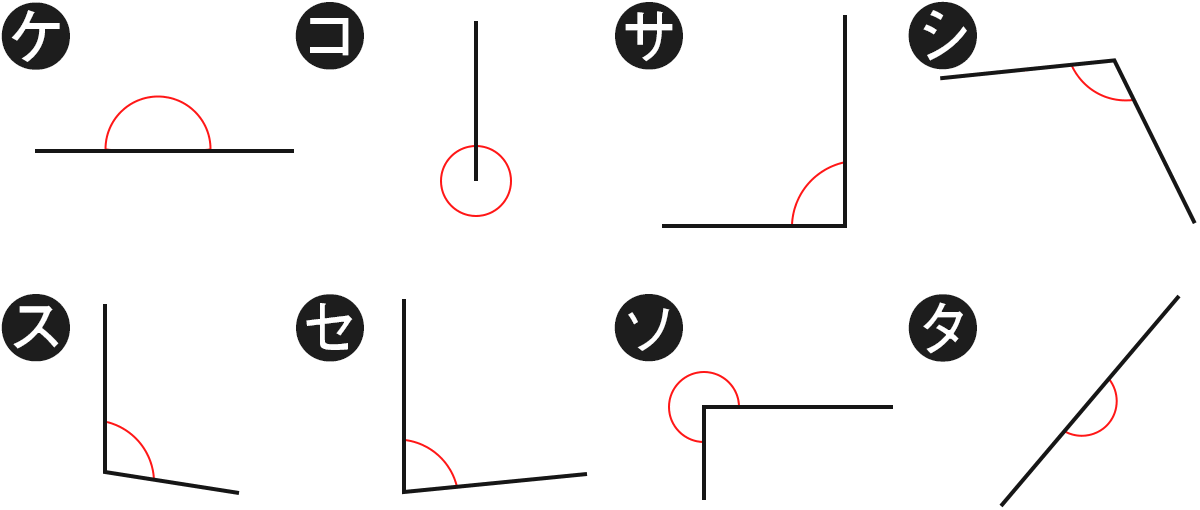
(ア)~(タ)の角度は つぎの3つのうちどれに当てはまりますか。
「 直角・直角より大きい・直角より小さい 」
答え方は 「 直角、大きい、小さい」でおねがいします。
おれたち三角形!
二等辺三角形と正三角形
なになに?
二等辺三角形と正三角形がどんな三角形なのか気になってしかたがないだって?

だれも気になってない
けど やる
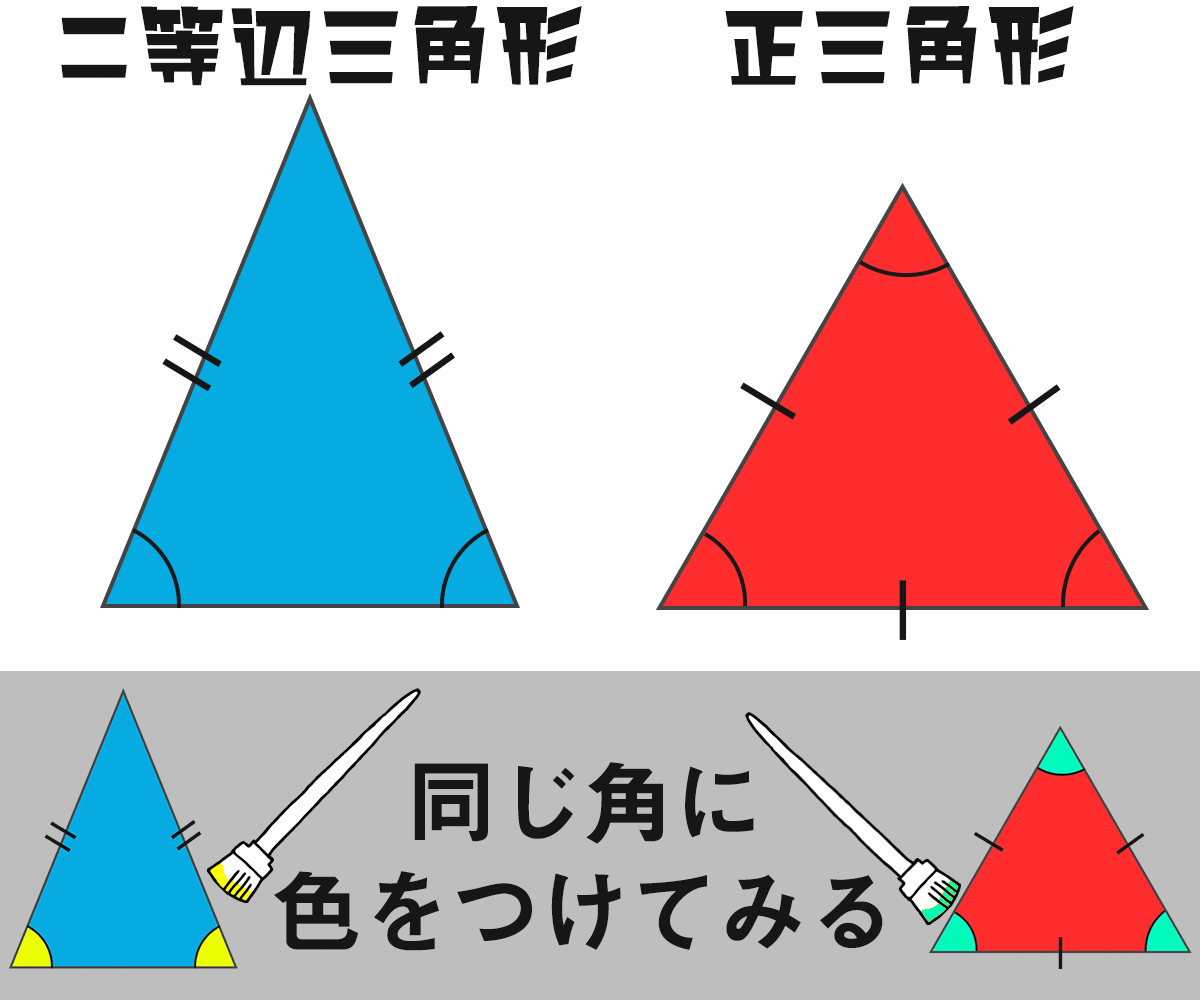
二等辺三角形
二等辺三角形とは、2つの辺の長さと 2つの角の大きさが等しい三角形
正三角形
正三角形とは、3つの辺の長さと 3つの角の大きさが等しい三角形

2つの辺と角が等しいのは 二等辺三角形
3つの辺と角が等しいのは 正三角形。
三角形を説明している文があります。□に入る言葉や数はなんでしょう。
答えは□をクリック
三角形が7つあります。下の問いに答えてね。じょうぎなどは使わず 見た目で答えること。
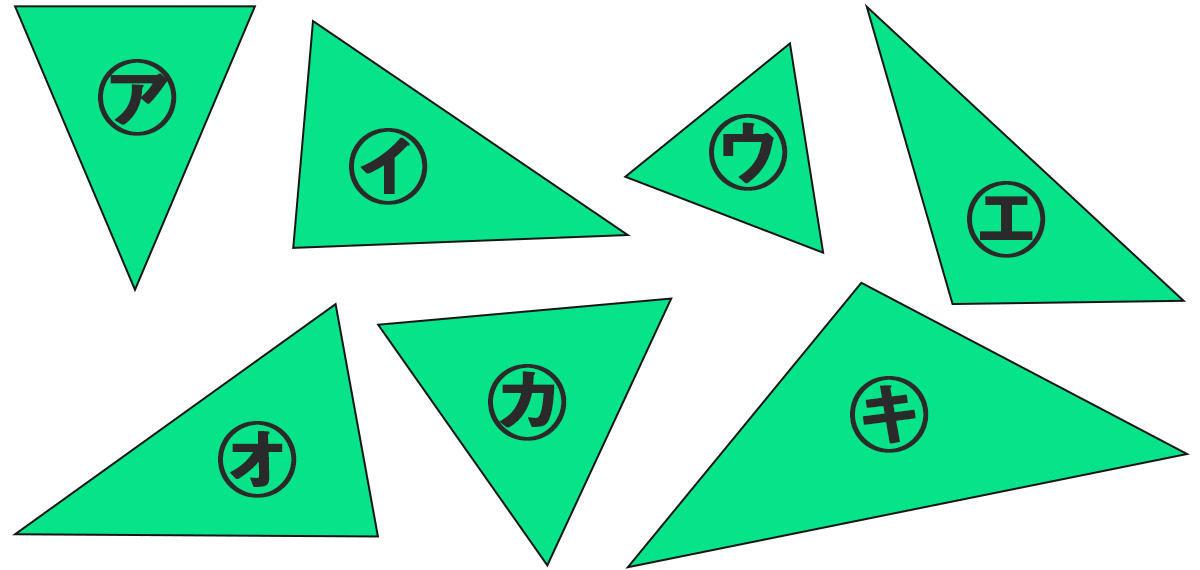
二等辺三角形をすべて答えよう
正三角形をすべて答えよう
まわりの長さが一番長い三角形はどれですか
この三角形の名前が分かるかな? フフフ 当ててみるがいい!
では、ちょっといじわるな問題出しちゃおう
正三角形は二等辺三角形でもある。○か×か
え?!

なぜなら、、
二等辺三角形は 「2つの辺の長さが等しい」 よね。
正三角形も2辺の長さが等しいではないか。

二等辺三角形のうち、さらに もうひとつの辺が等しいのが正三角形 というわけです。
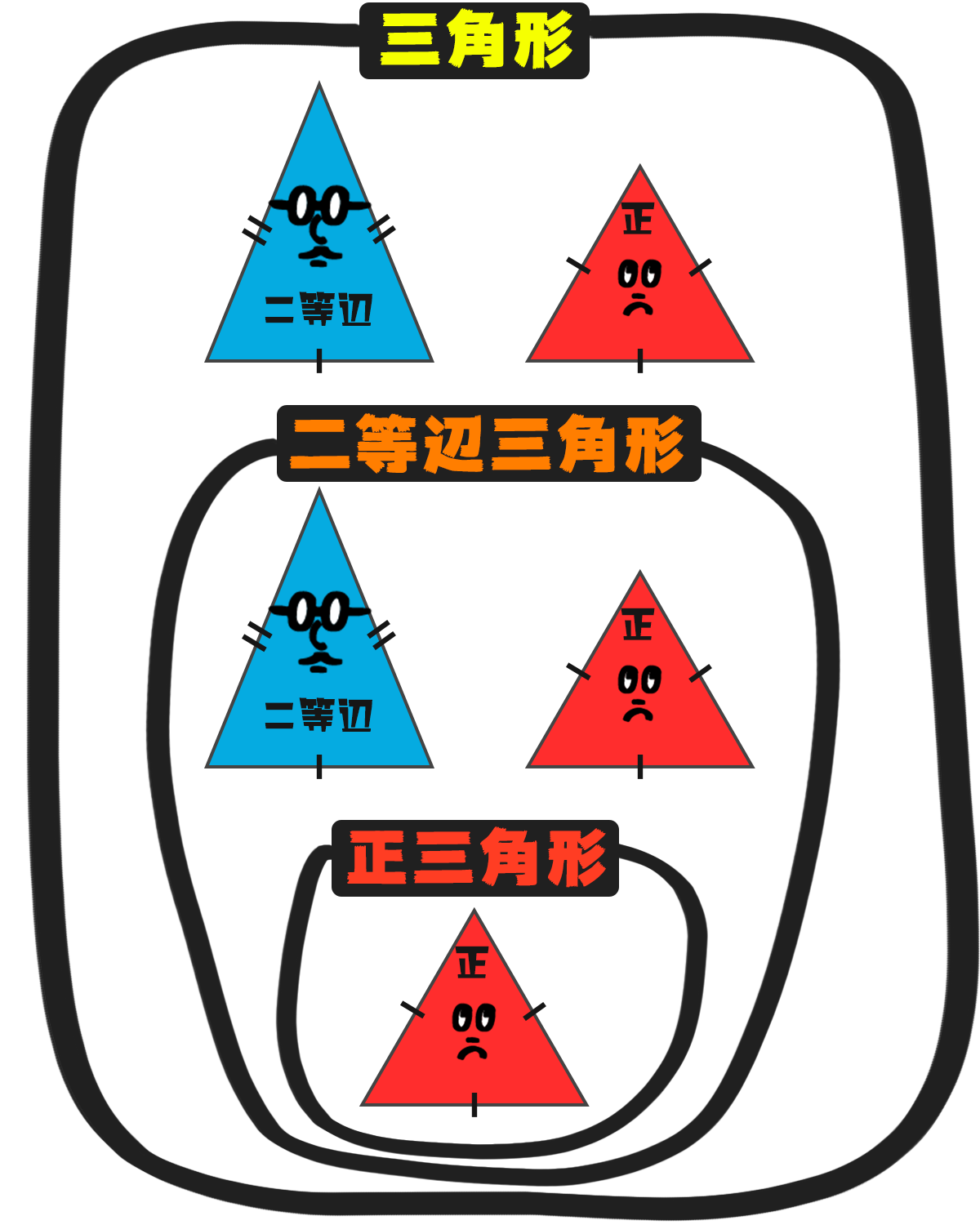
二等辺三角形の中でも 3辺の長さが等しい とくべつな三角形が 正三角形

つぎのような正三角形の辺の長さをおしえて!
1辺の長さが4cmの正三角形があります。この正三角形のまわりの長さは何cmですか。
1辺の長さが12cmの正三角形があります。この正三角形のまわりの長さは何cmですか。
まわりの長さが60cmの正三角形があります。この正三角形の1辺の長さは何cmですか。
二等辺三角形の辺の長さをおしえて!
まわりの長さが10cmの二等辺三角形があります。長さが等しい辺はそれぞれ3cmです。のこりの辺の長さは何cmですか。
答えをくわしく
問題をそのまま図にしてみると分かりやすい
❶ まわりの長さが10cmの二等辺三角形
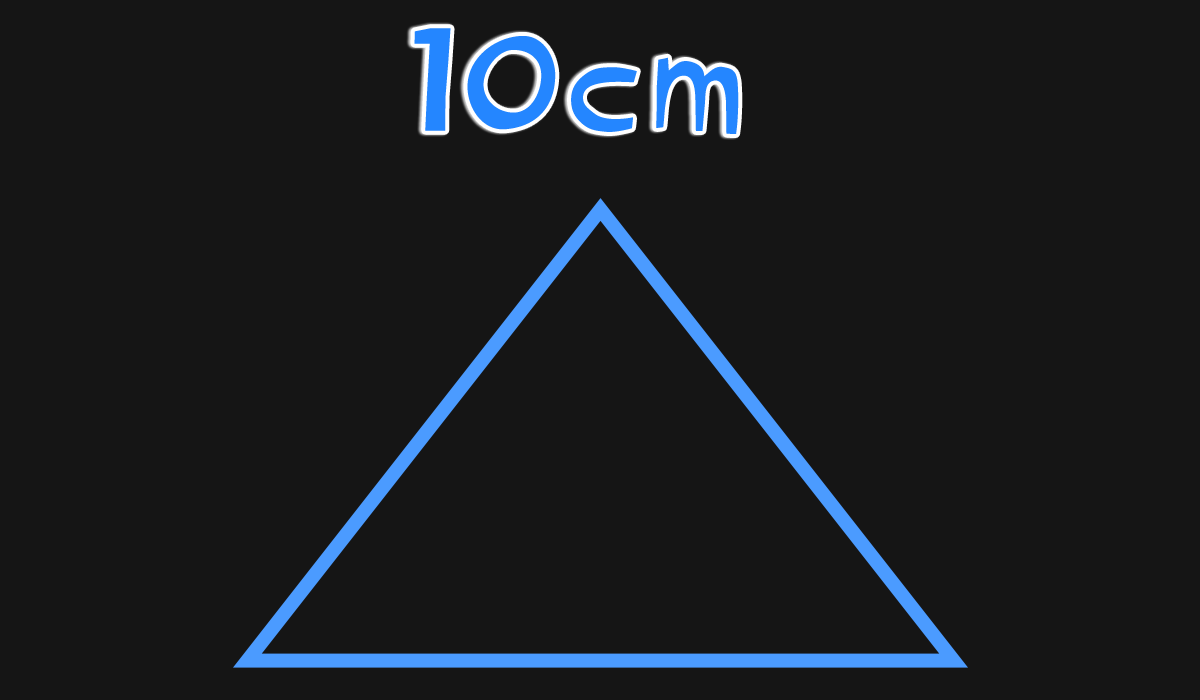
❷ 長さが等しい辺はそれぞれ3cm
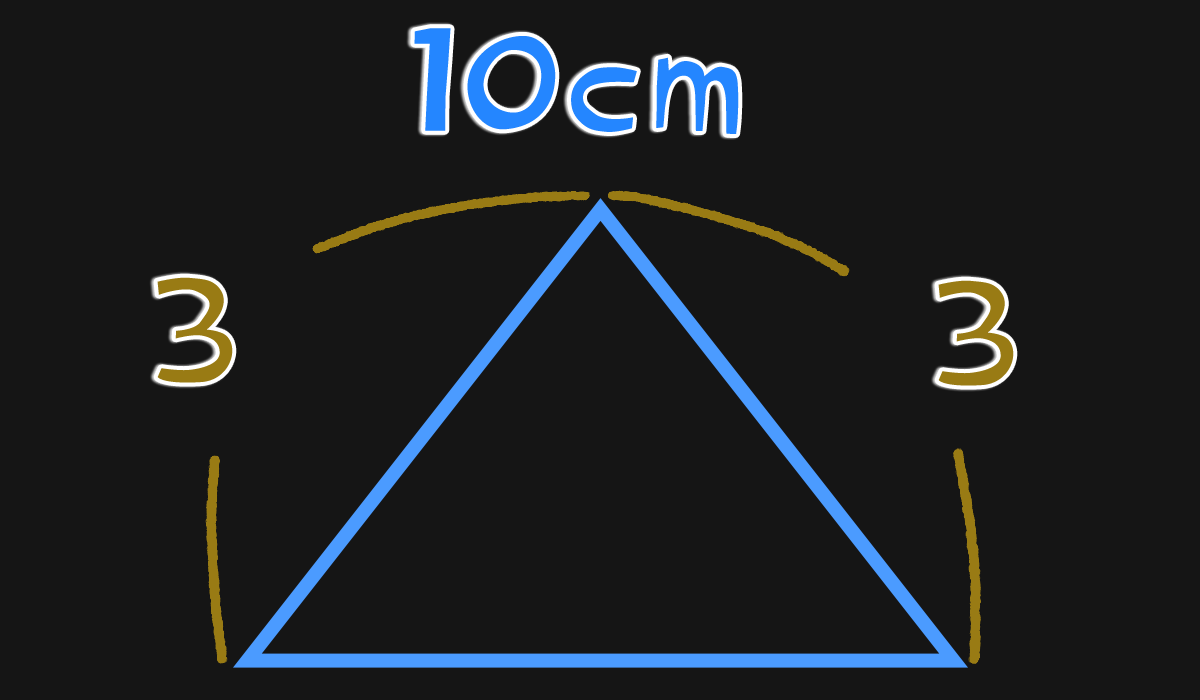
❸ のこりの辺の長さは何cmか
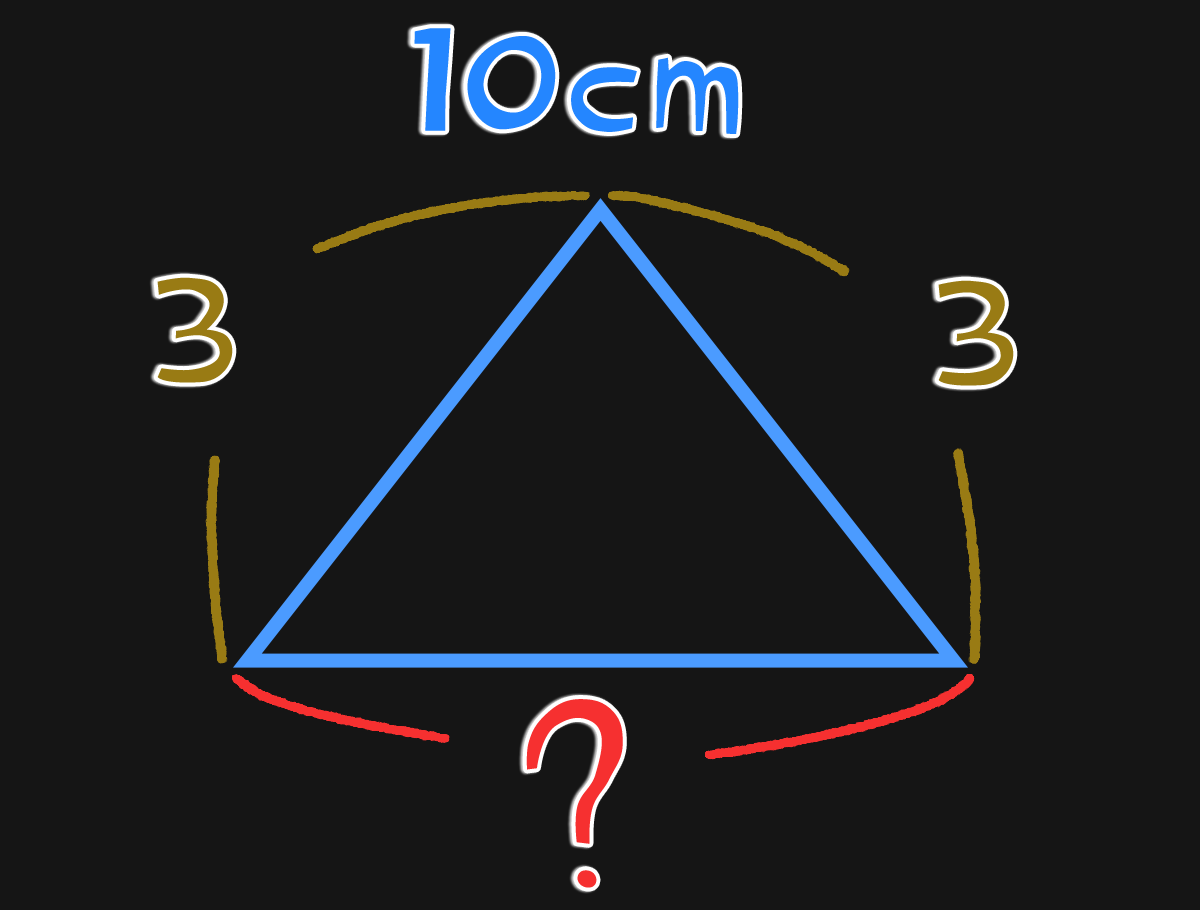
3+3=6
10-6=4
かっこを使う式だと
10-(3+3)=4
かっこの中は先に計算する!ってきまりがあるから 3+3 からやる。
まわりの長さが15cmの二等辺三角形があります。長さが等しい辺はそれぞれ6cmです。のこりの辺の長さは何cmですか。
まわりの長さが23cmの二等辺三角形があります。長さが等しい辺はそれぞれ8cmです。のこりの辺の長さは何cmですか。
まわりの長さが50cmの二等辺三角形があります。長さが等しい辺はそれぞれ15cmです。のこりの辺の長さは何cmですか。
長方形の紙を二つに折って 直線アイで切り、開いたときにできる三角形について
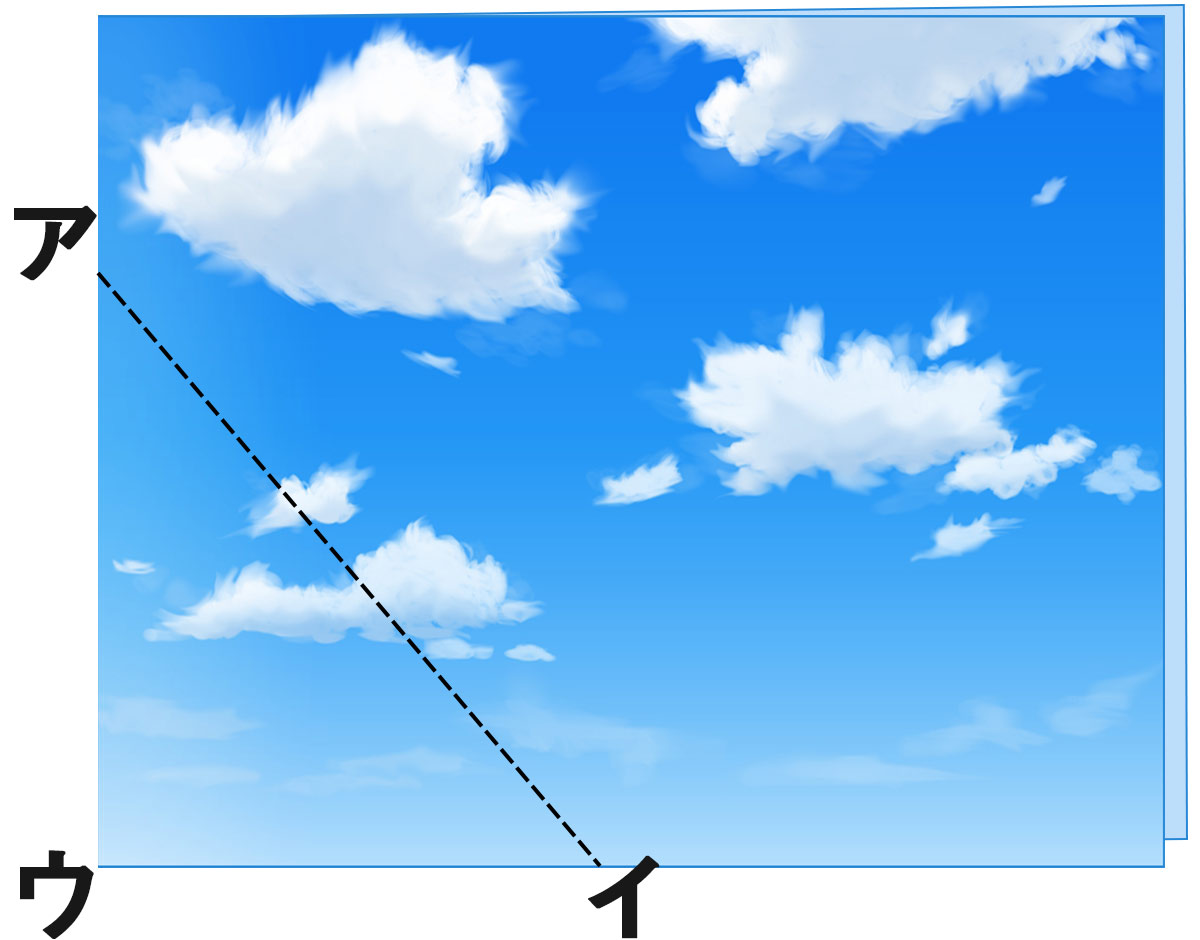
直線アイで切り、開いたときに正三角形にします。直線アイがつぎの長さのとき、直線イウは何cmですか。

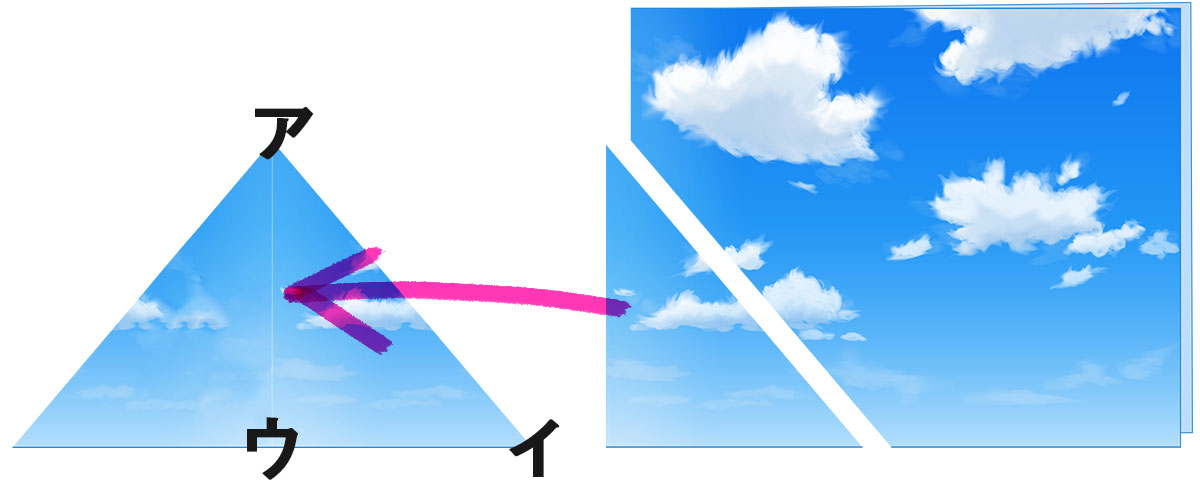
アイウが つぎの長さのとき、開いたときにできる三角形の名前は何ですか。
パッと開くと、
こんな感じの三角形ができます。
三角形はできる?できない?
3本のぼうを使って三角形を作る。三角形ができるものには「できる」、三角形ができないものには「できない」と答えるんだ。たのむぞ!
三角形ができるかの見分けかた
3本のうち みじかい辺2本を足して、一番長い辺より長くなれば 三角形はできます!
ありゃ かんたん。じゃあ やってみますよ
三角形になる!

3本のうち みじかい辺2本を足す。それが 一番長い辺より長くなれば 三角形になる。

みじかいのは、一番下と まん中。
それを足すと、、1番長い辺より長くなるね
ってことは
三角形になる!
三角形にならない・・
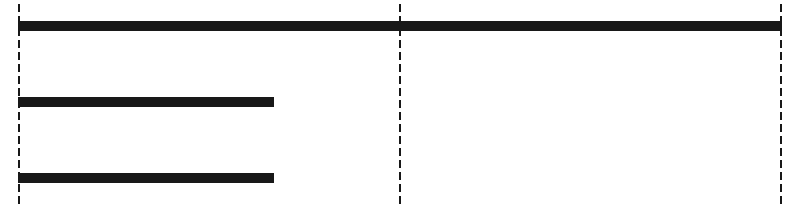
一番下と まん中の辺を足しても 長い辺より みじかい。これは 三角形にならない。
あと これ!
足すと 長いぼうと同じ長さになるやつ

1番上と まん中のぼうを足すと、長いぼうと同じ長さでしょ。
角やちょう点が作れないから 三角形にはならない!
では、とき方が分かったところで、同じ問題だけど~~ちょっとだけちがう問題にチャレンジしてもらおう
これが最後の問題です!