小学生におすすめの立体図形で頭の体操

立体図形 「直方体と立方体」を使って頭の体操しましょう

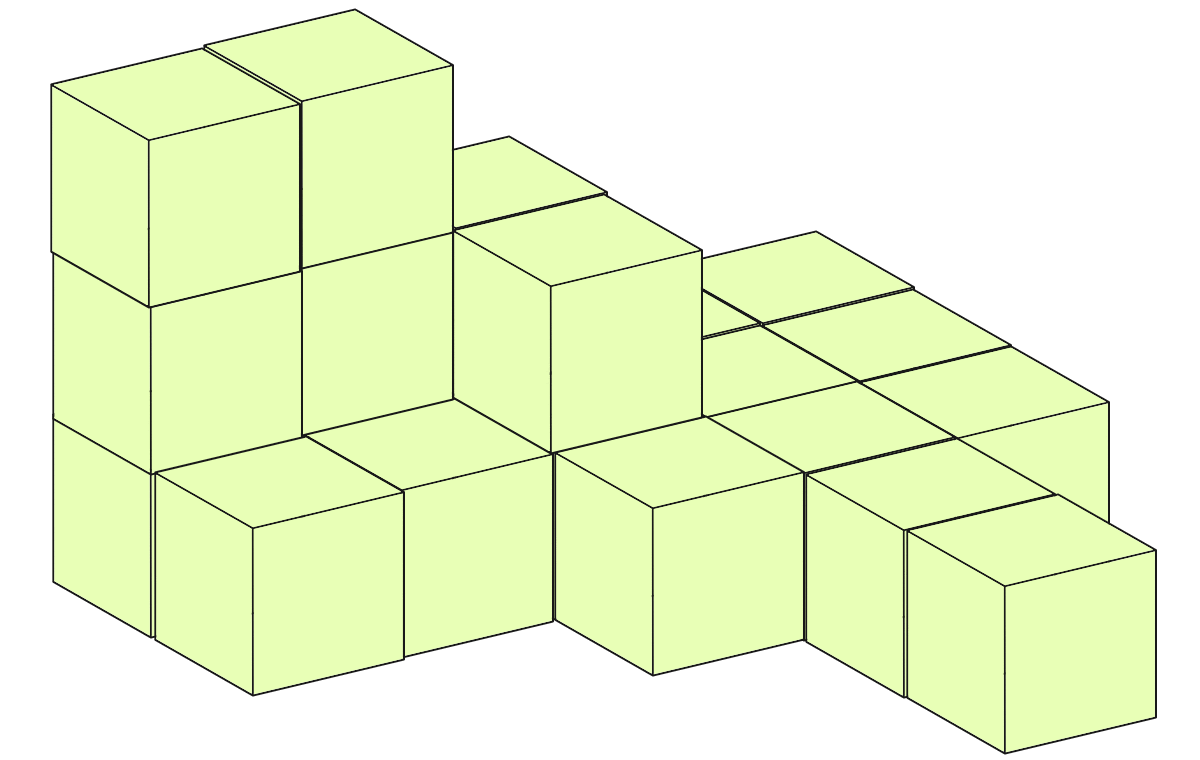
積み重なったブロックなど色んな問題を出します
直方体と立方体で楽しく考えよう。いくぞ!
直方体と立方体のいろんな問題
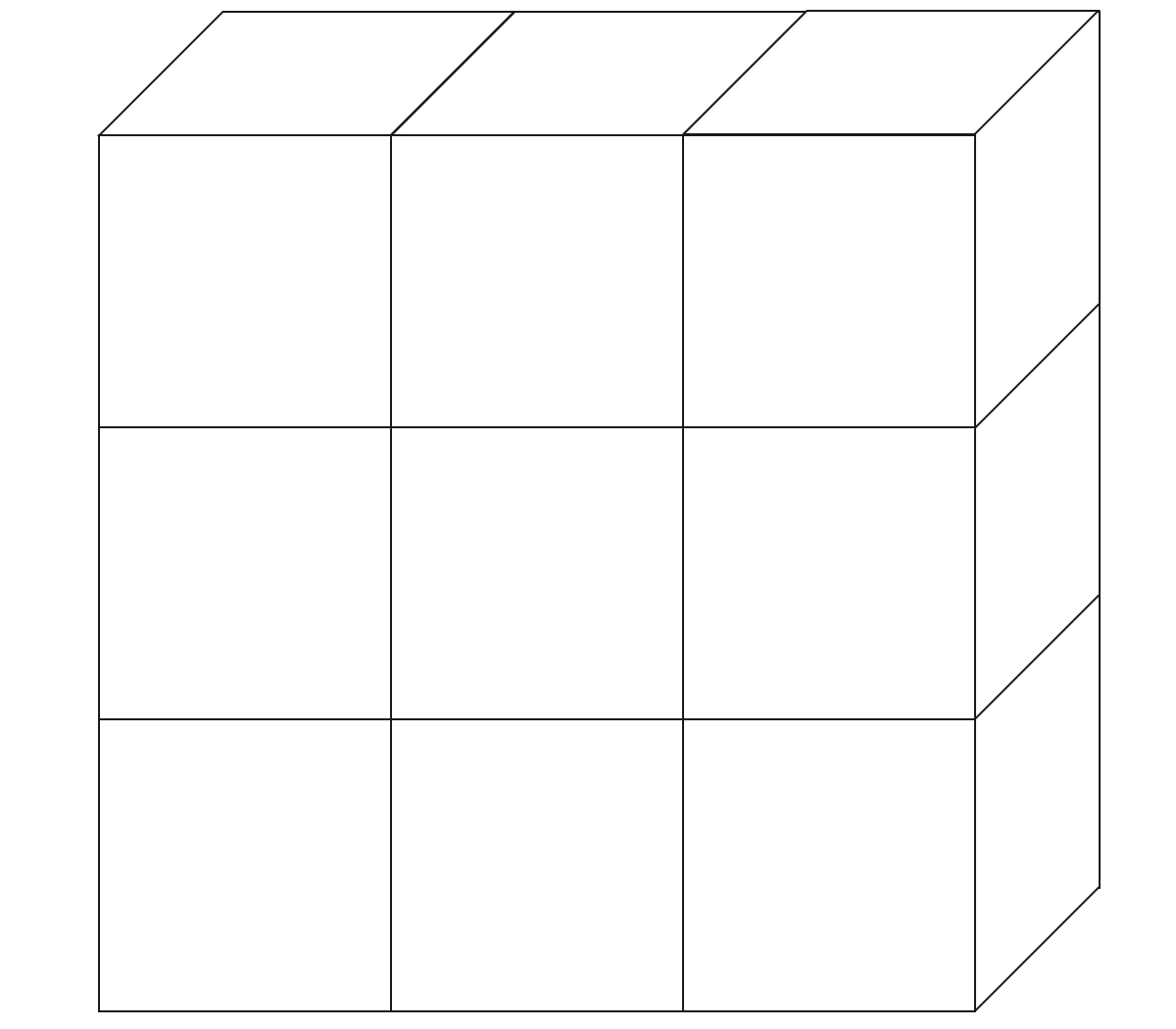
立方体を9個使って直方体を作りました。
この直方体の表面に色を塗りまーす
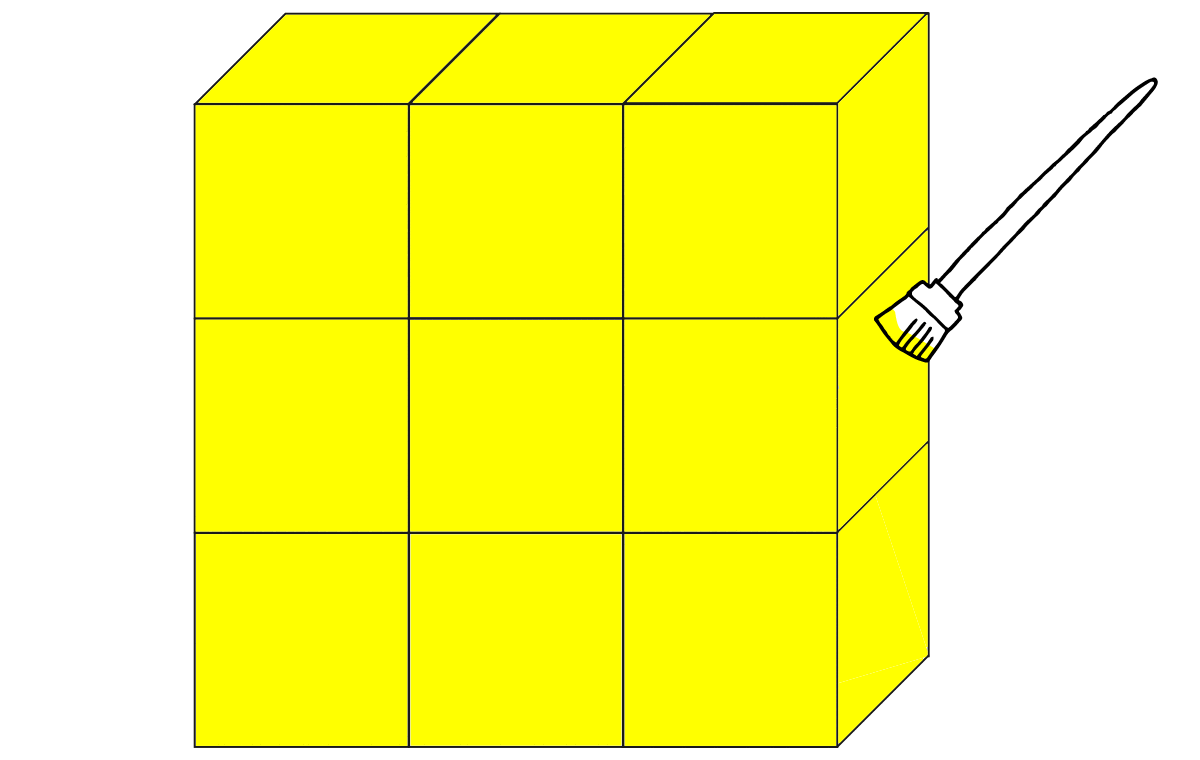
きれいに塗れたところで・・・さあ問題です!
次のような立方体は何個ありますか。
答えは□をクリック
答えをくわしく
4面、3面、2面、それぞれこの位置だね
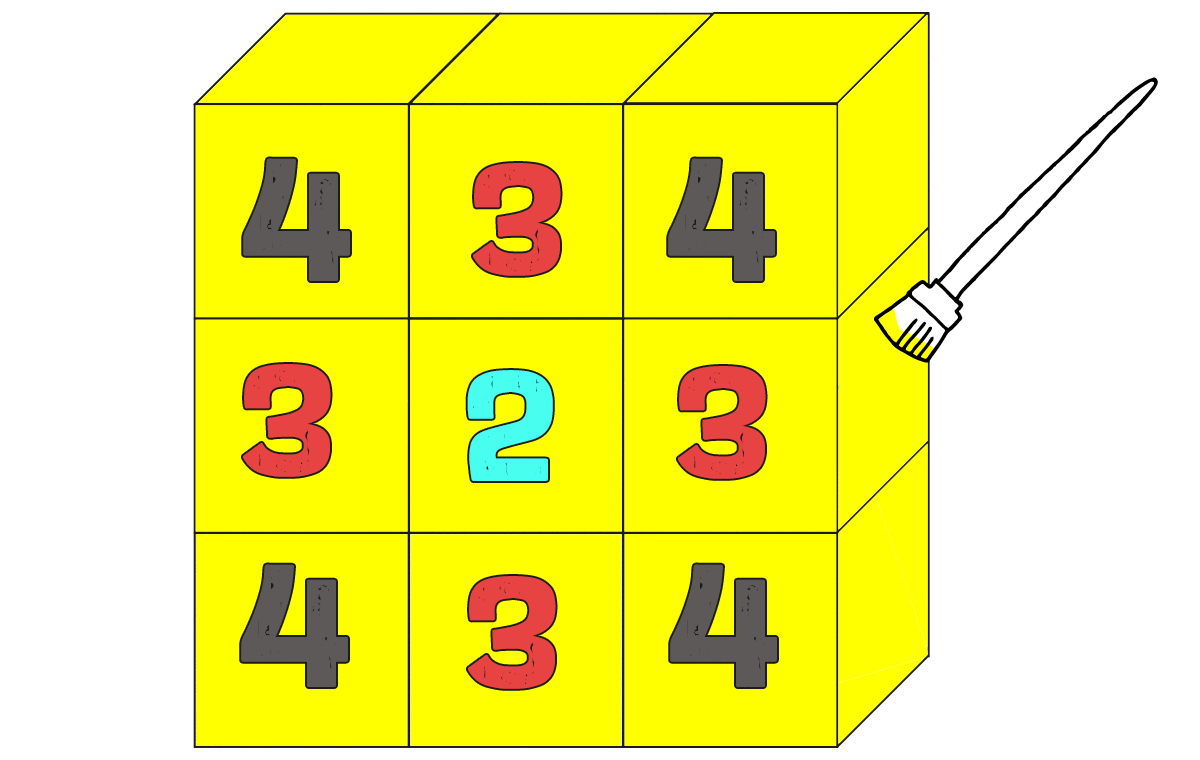
なんか規則性あるね。ならび方にパターンがありあり
下の図のように ブロックを16個ならべて直方体を作り、表面に色をぬりました。16個のブロックのうち、次のようなものは何個ありますか。
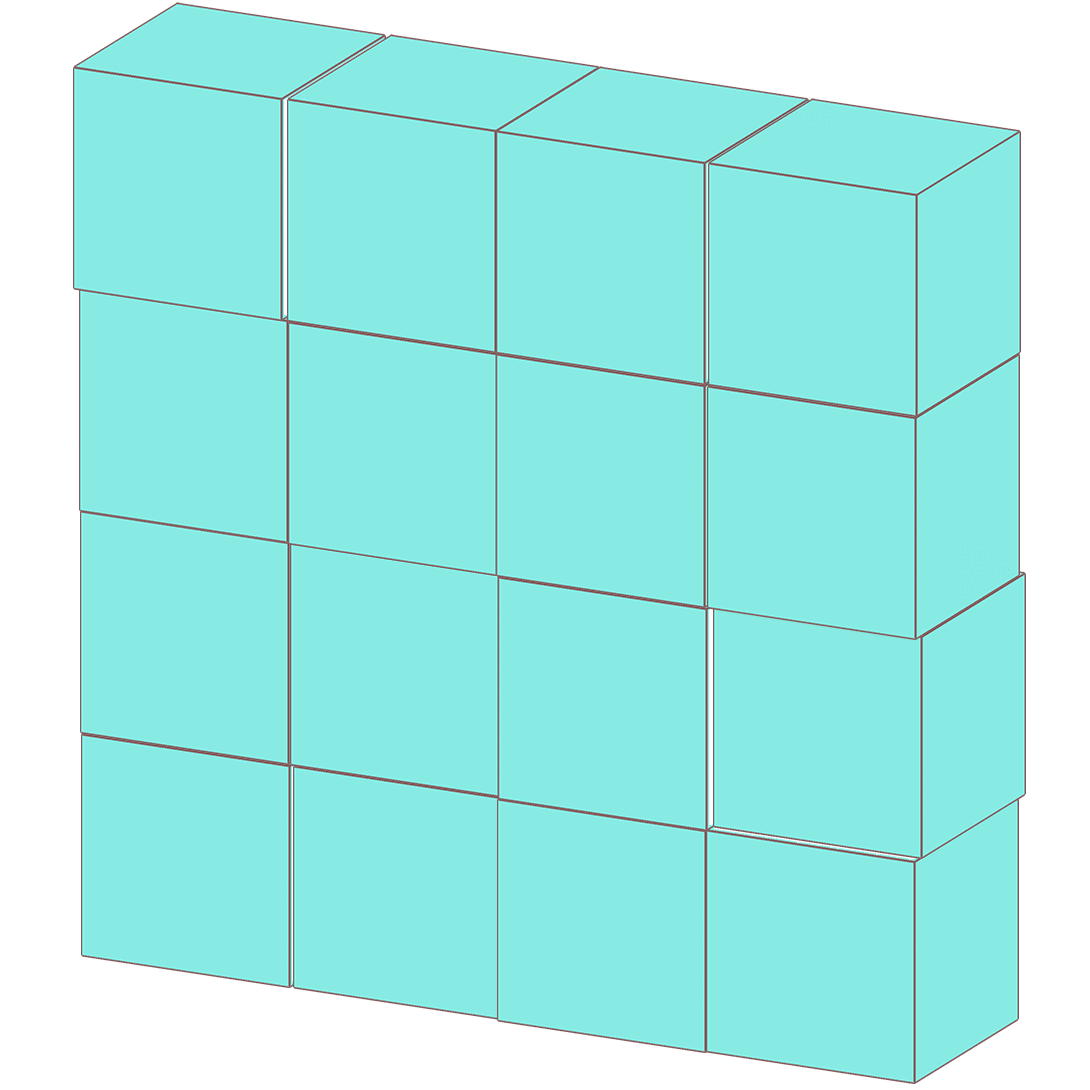
ちょうしに乗って 100個のブロックで直方体を作り、表面を黄色にぬりました。縦に10個、横に10個並べてあります。次のようなものは何個ありますか。
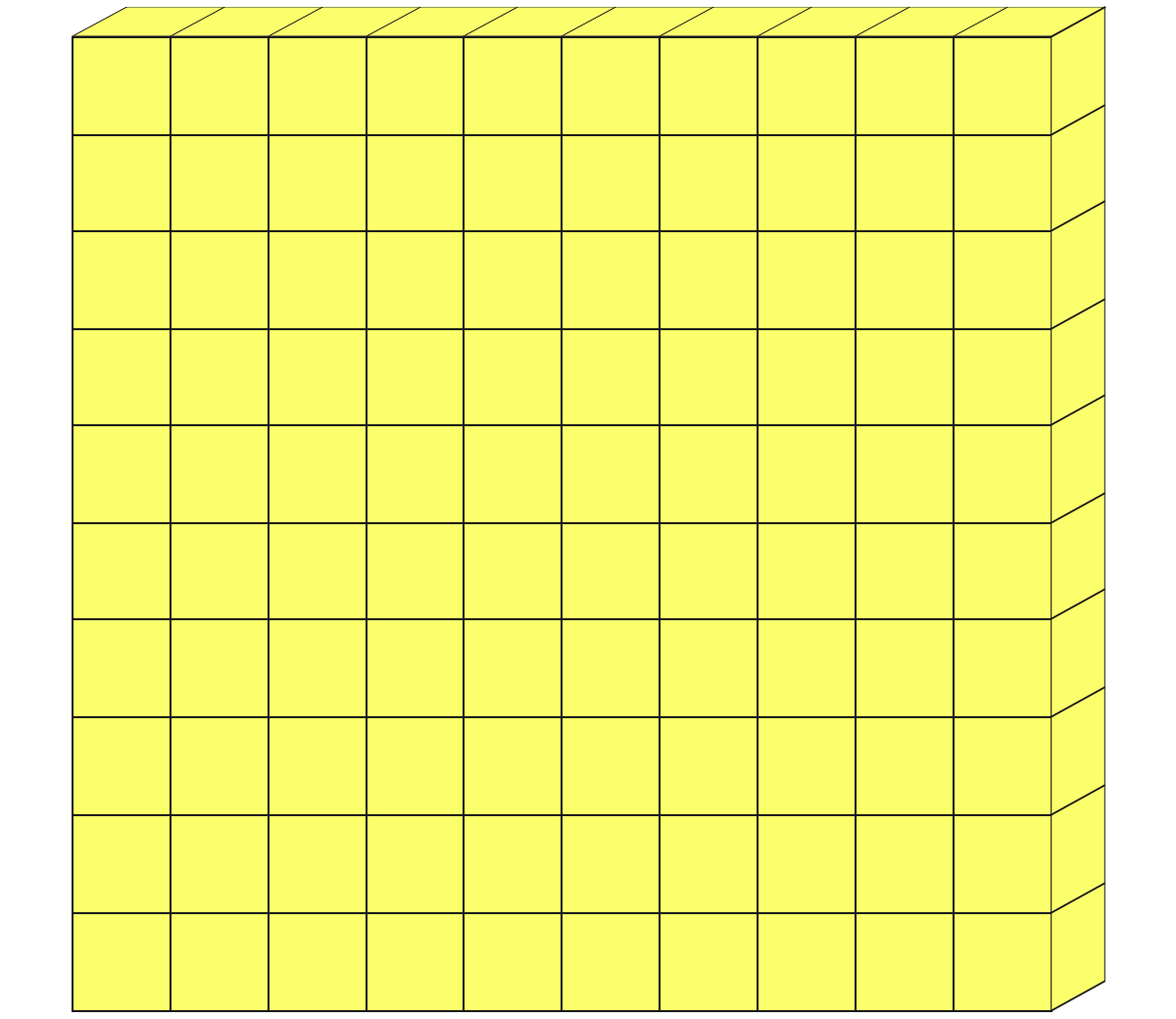
数えなくてもわかるぜ
4面、3面、2面で色分けしてみます。
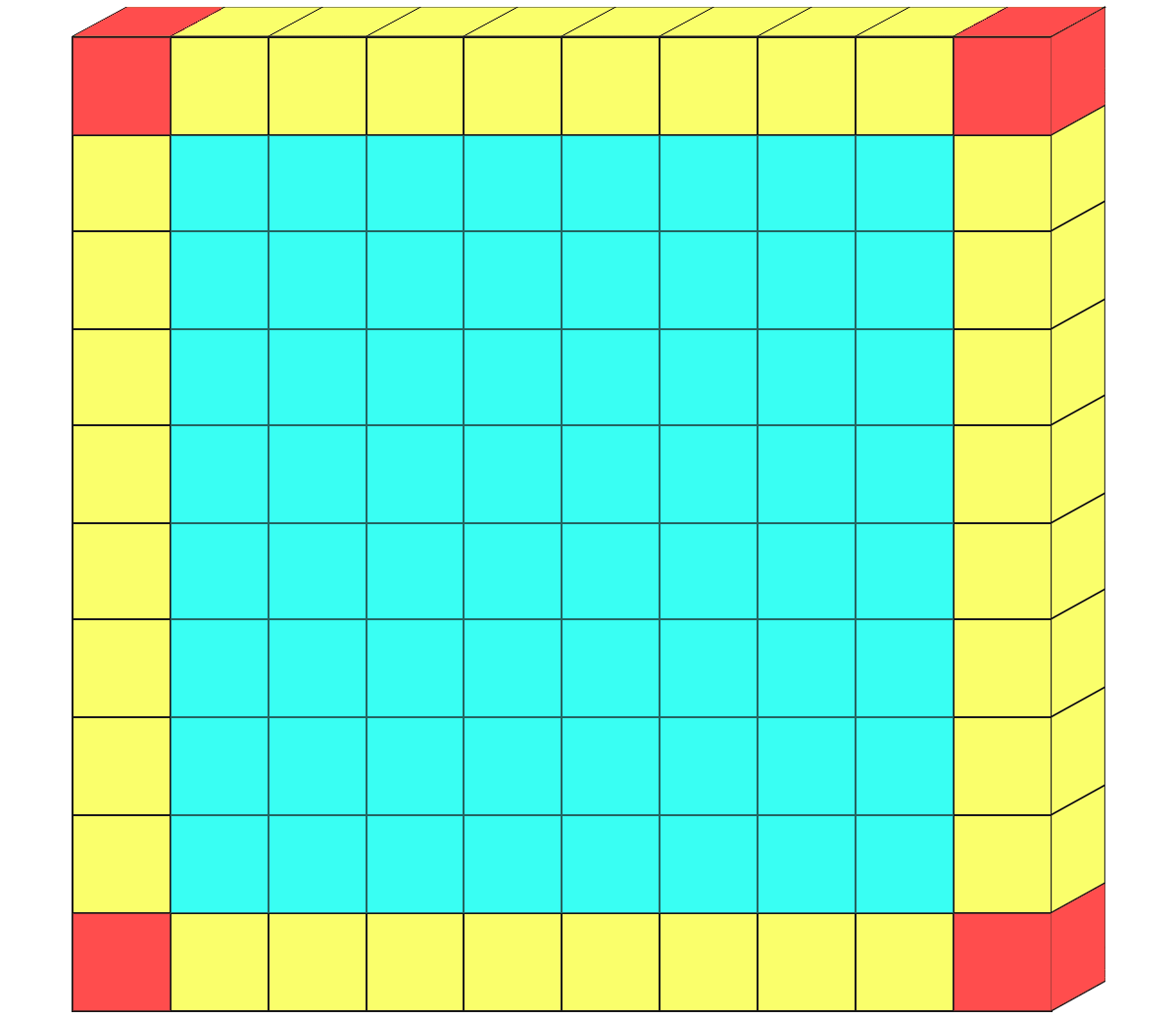
4つの面に色が塗られたブロックは赤のところ、角の4個。
3つの面に色が塗られたブロックは黄色。8個のかたまりが4つあるので
8×4=32
2つの面に色が塗られたブロックは、
8×8=64
小さな立方体のブロックを並べて大きな立方体を作り、表面に色を塗りました。小さな立方体のうち、次のようなものは何個ありますか。

つみ木は何個消えた?

分かったら教えてー
- (1)
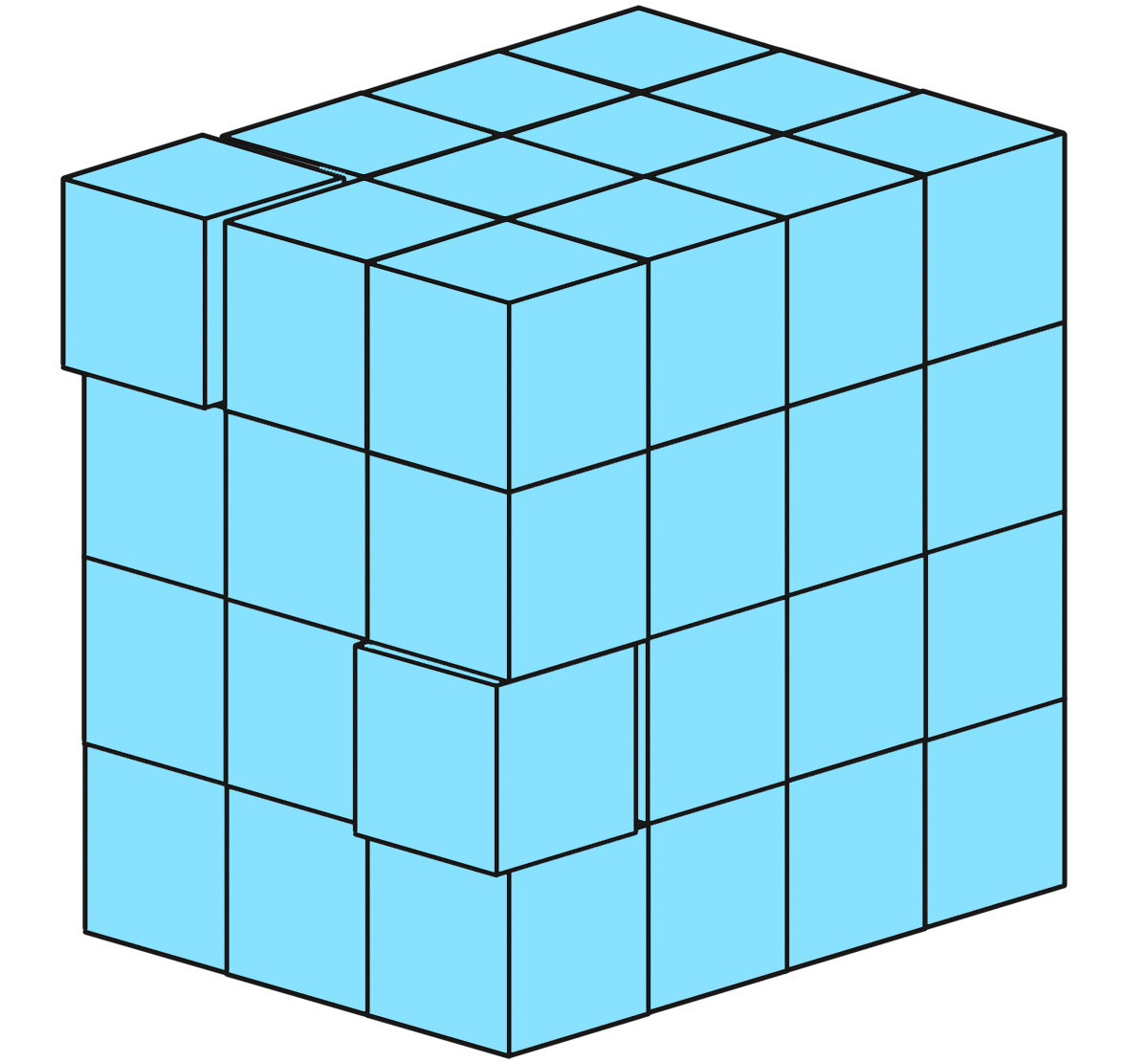
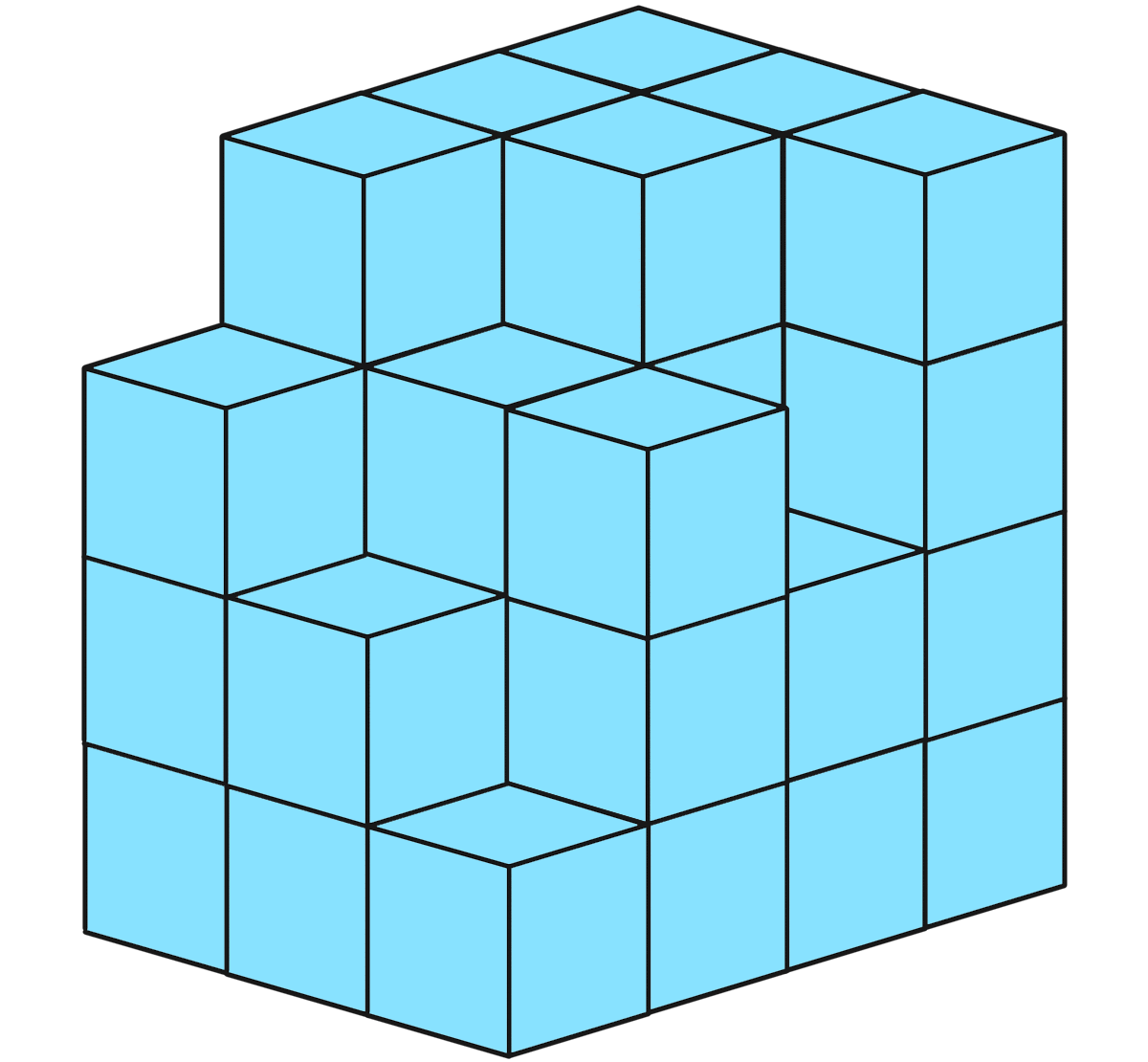
- (2)
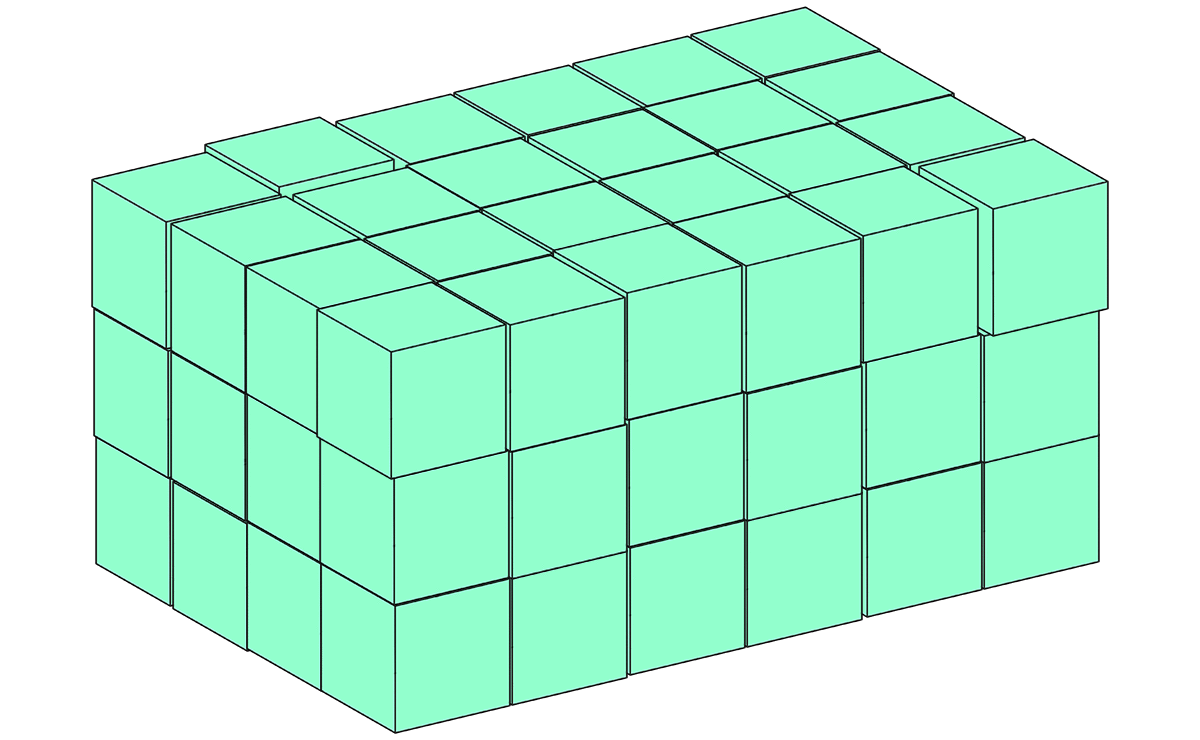
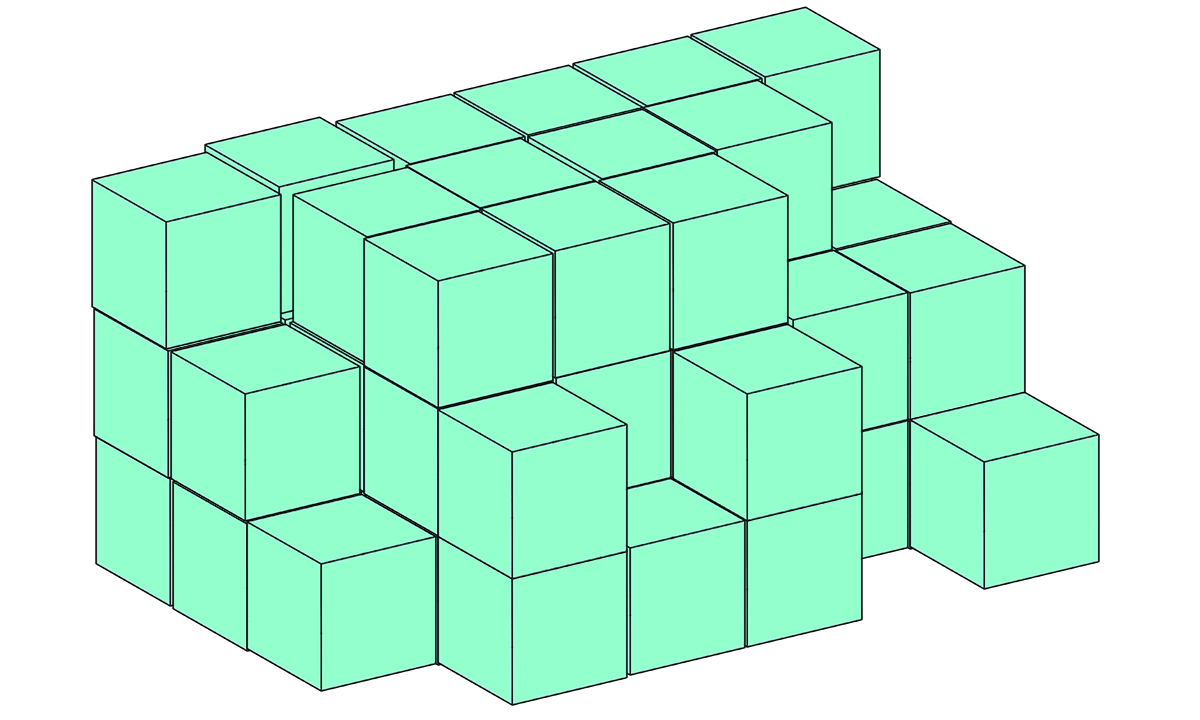
さいころを組み立てろ!
さいころを組み立てたとき、(あ)(い)(う)に入る数字は何でしょう。

さいころは、向かい合う面の合計が「7」って決まってる
- (1)
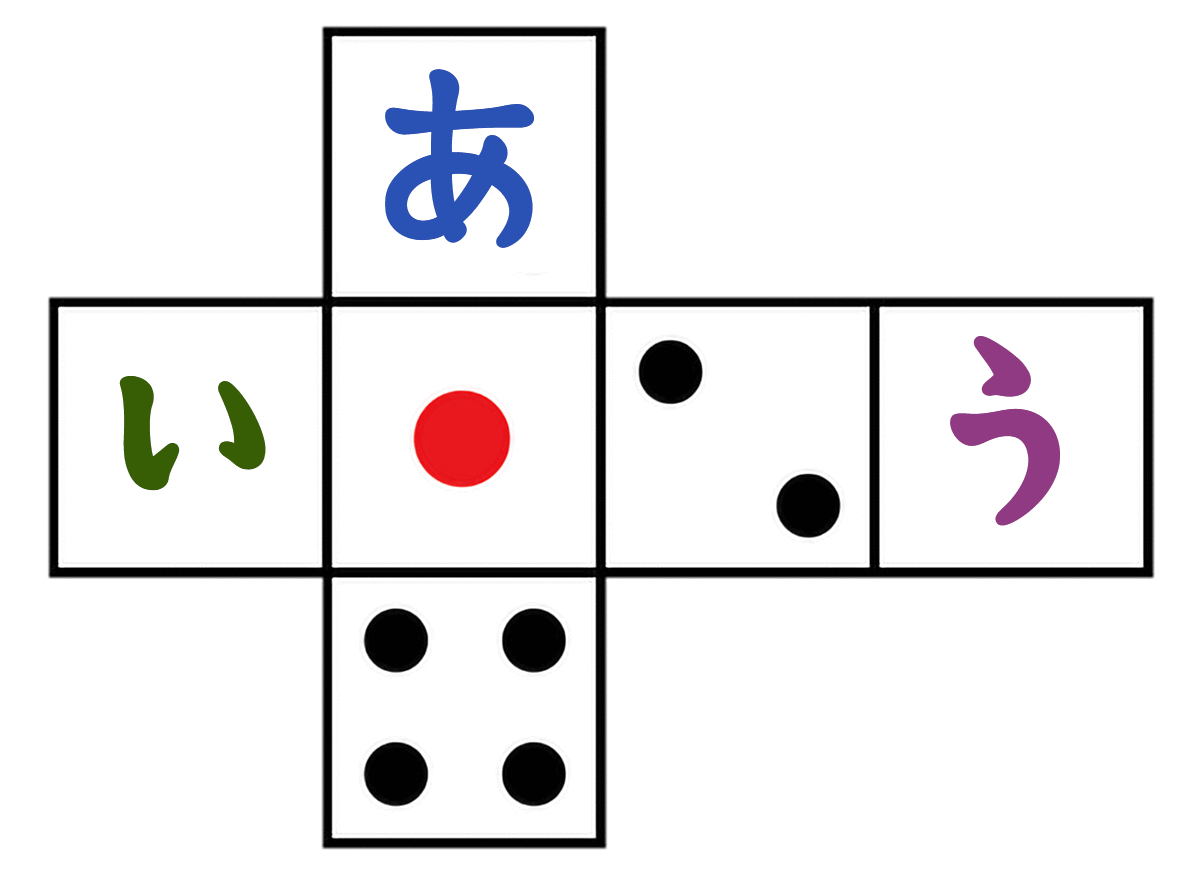
- (2)
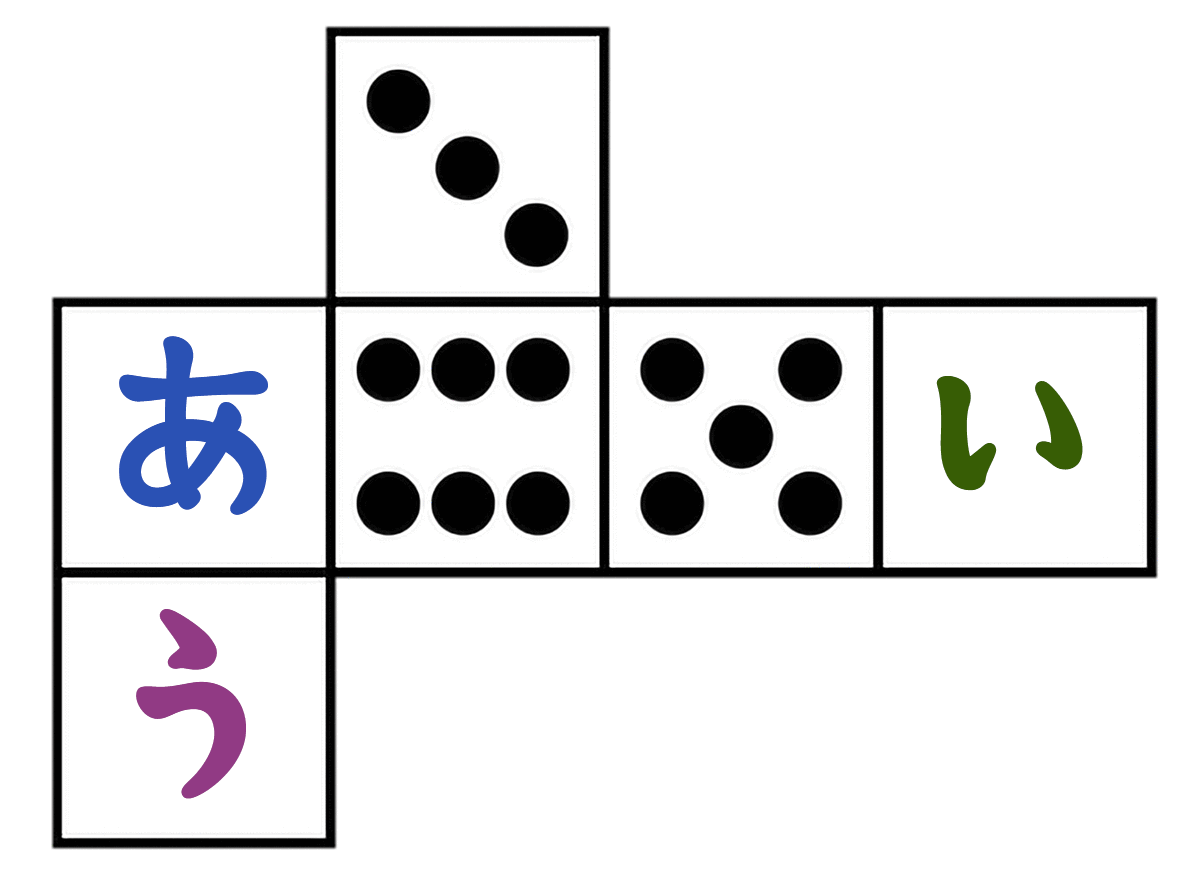
- (3)
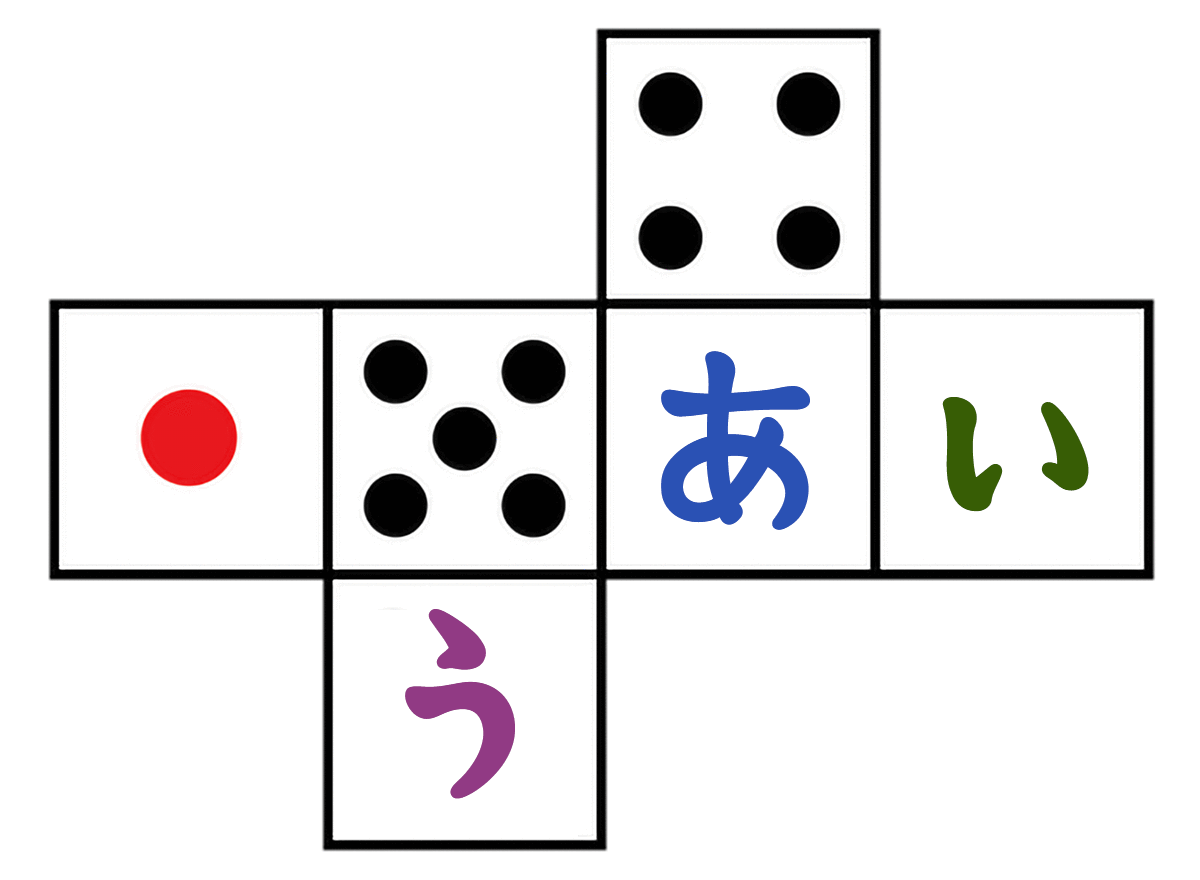
- (4)
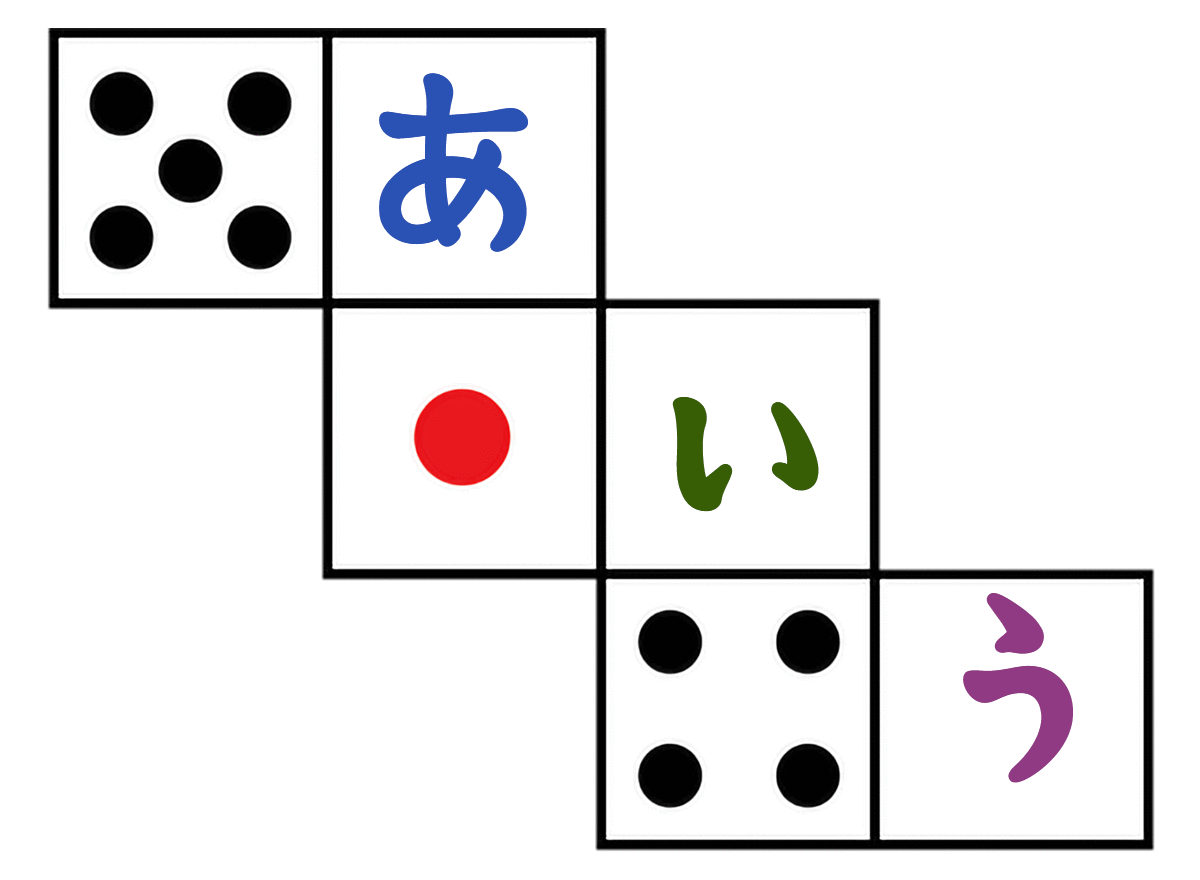
- (5)
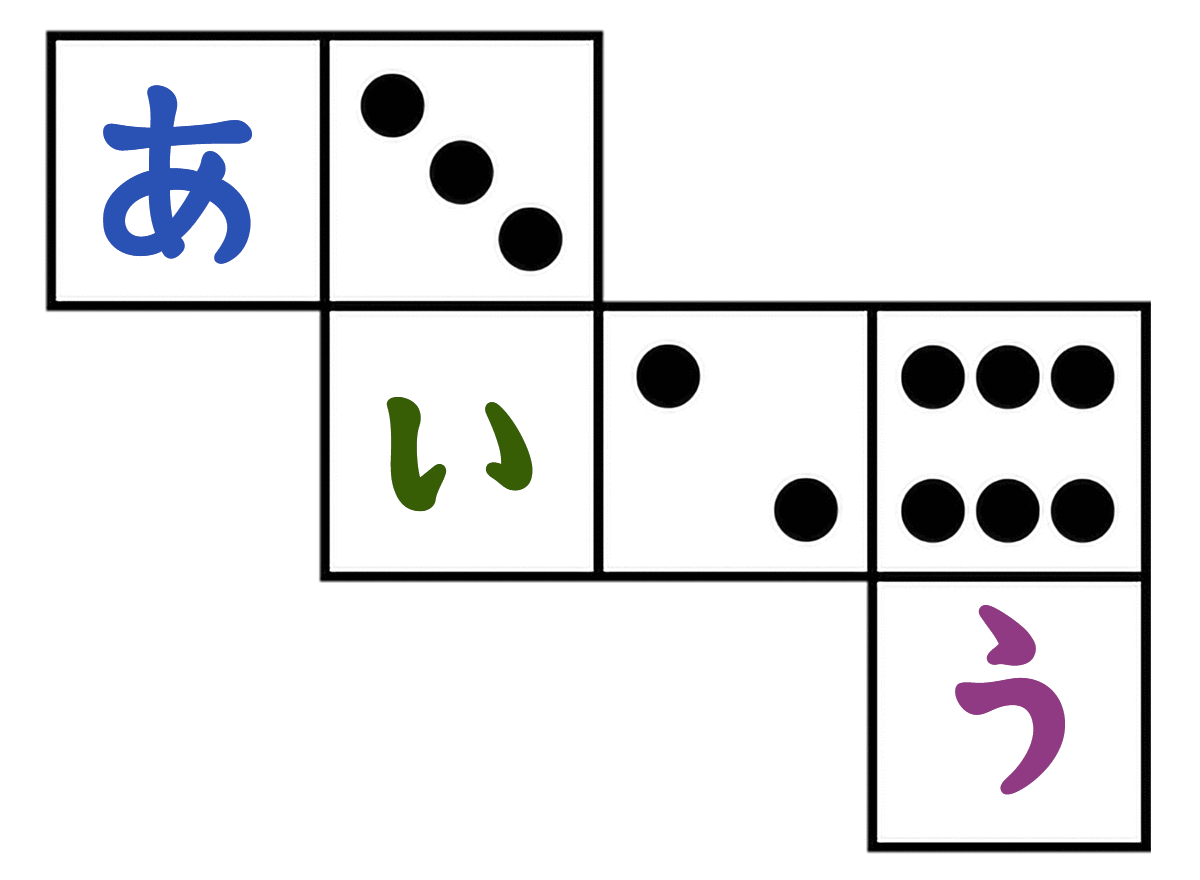
- (6)
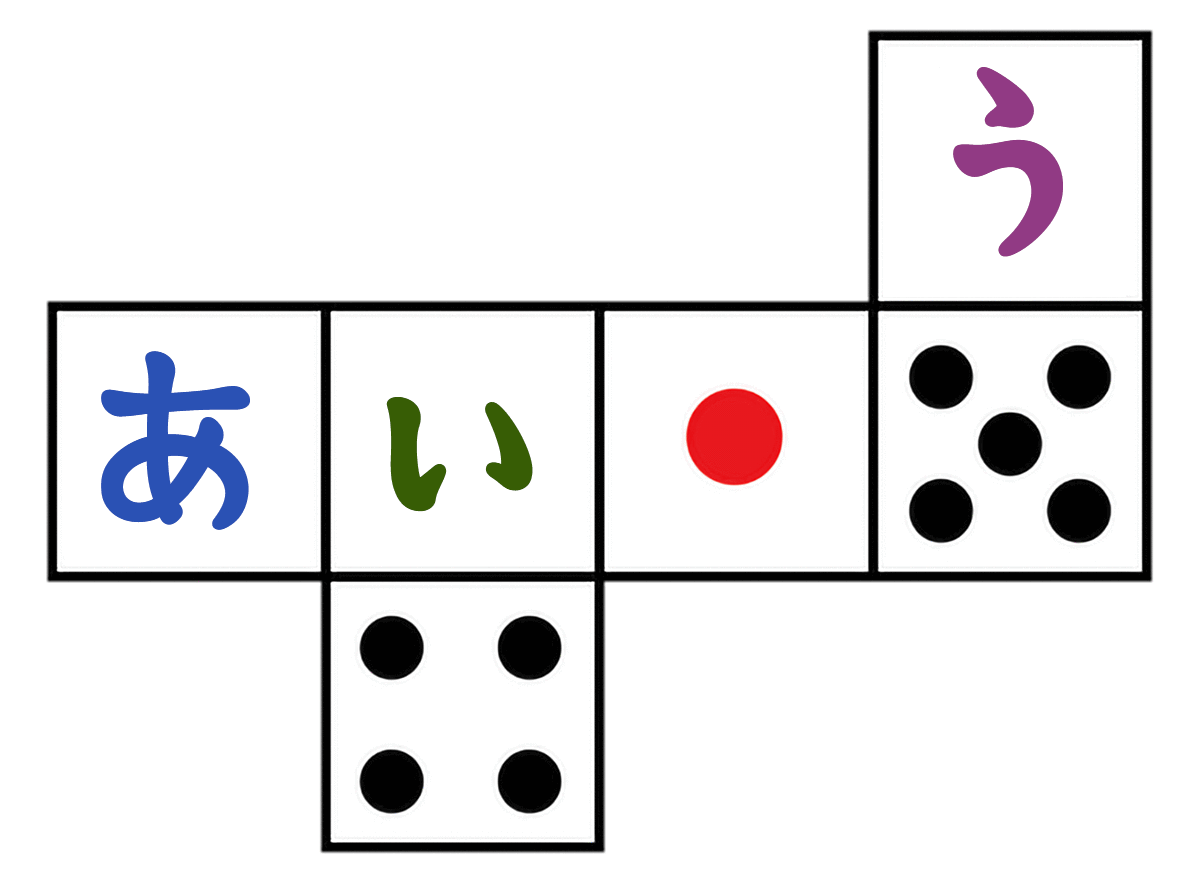
- (7)
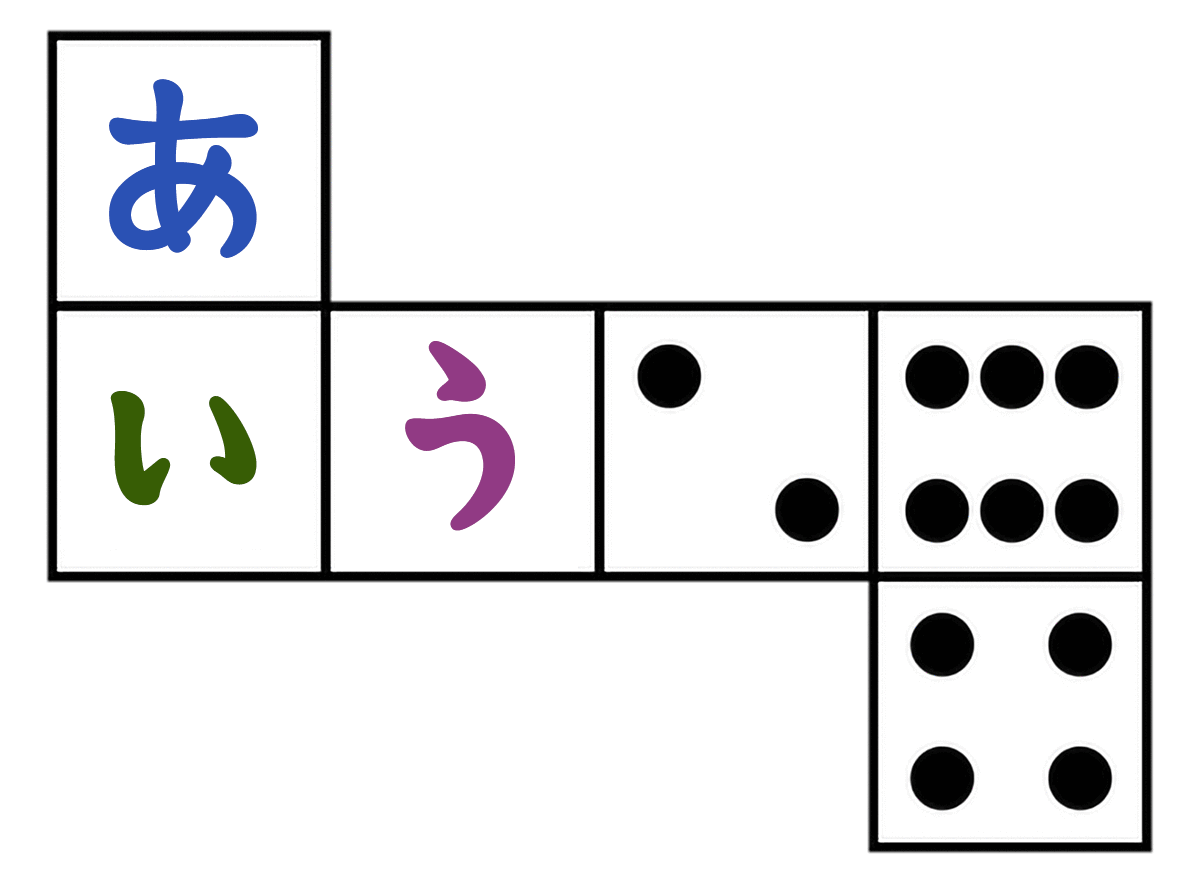
- (8)
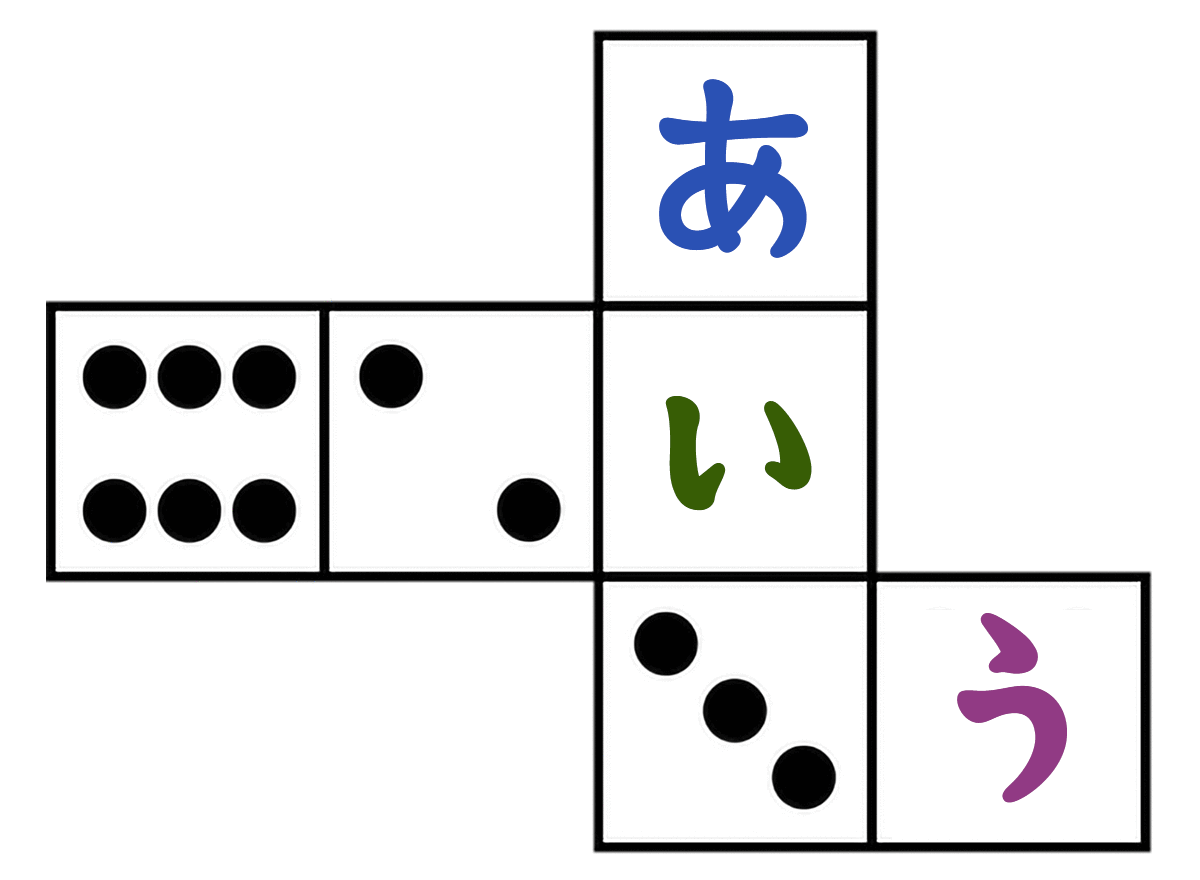
- (9)
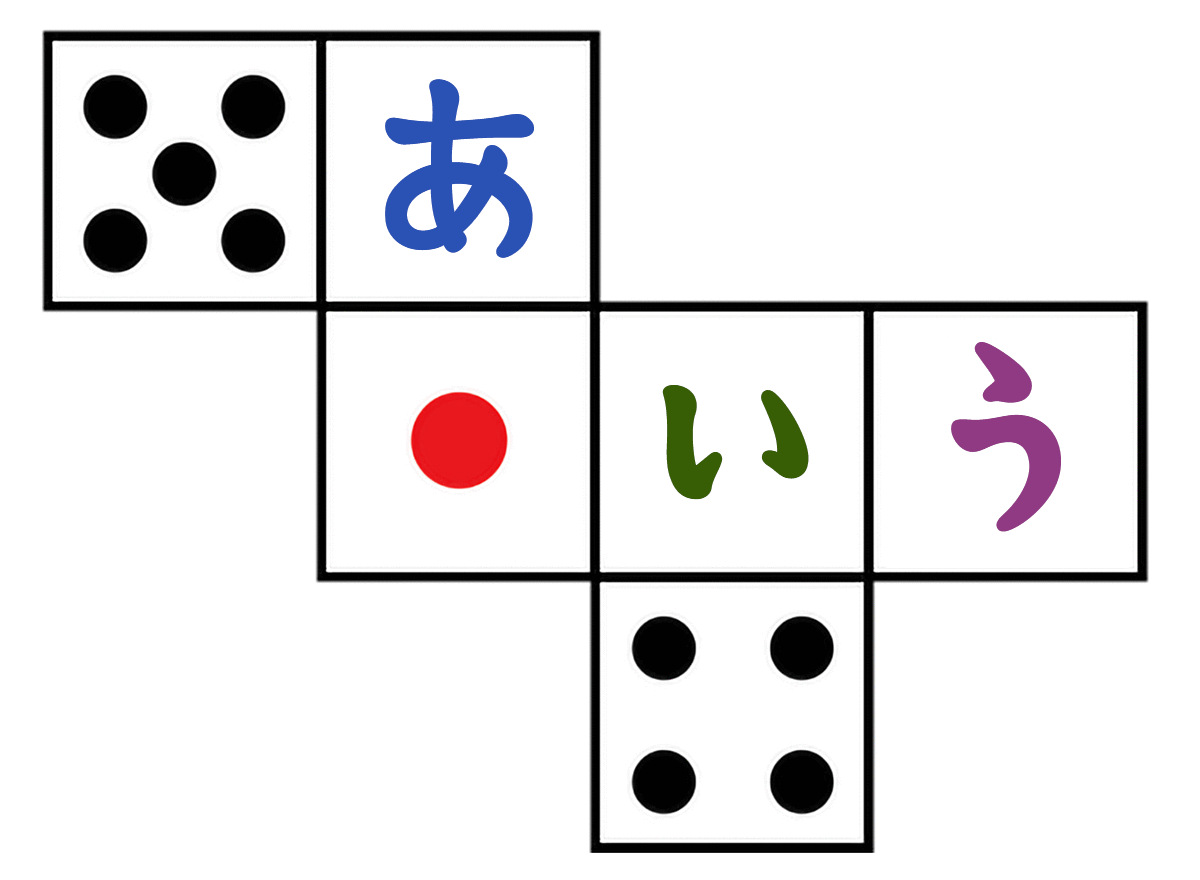
- (10)
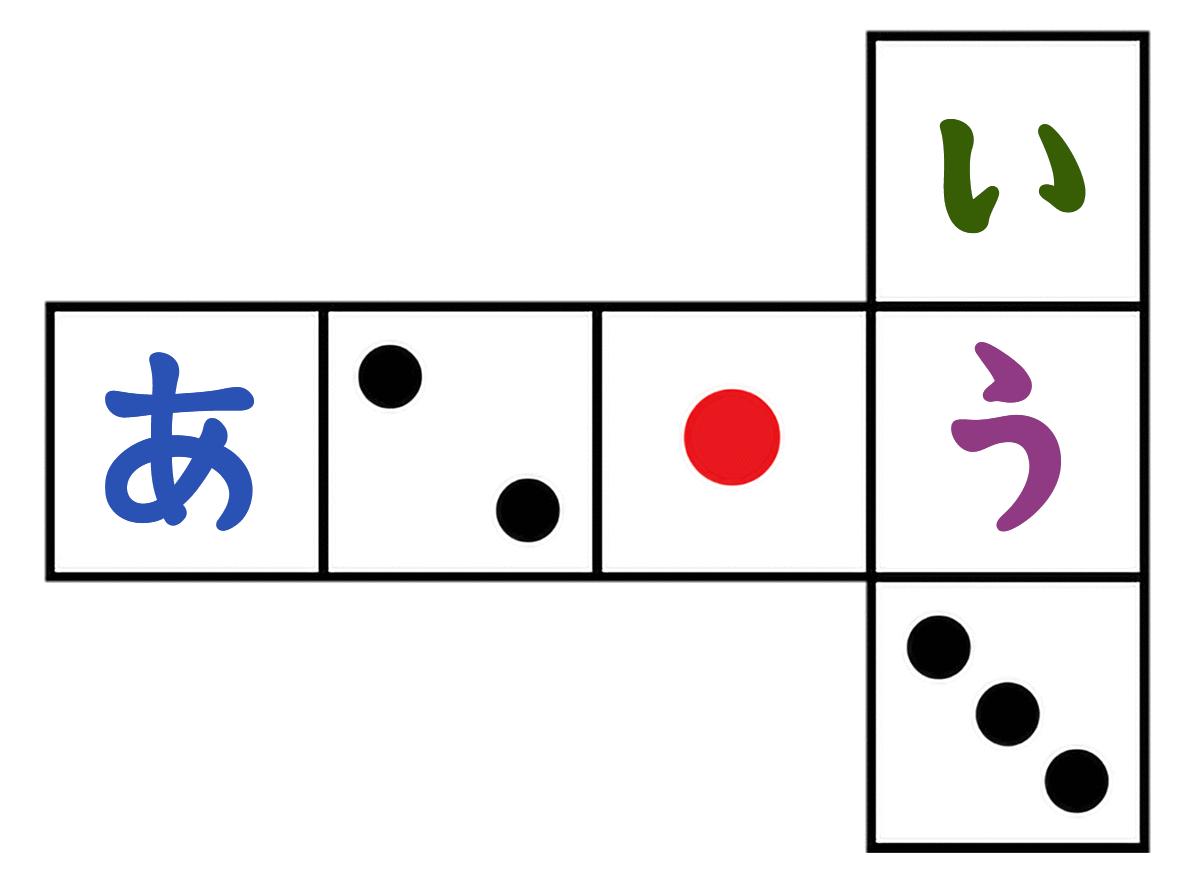
- (11)
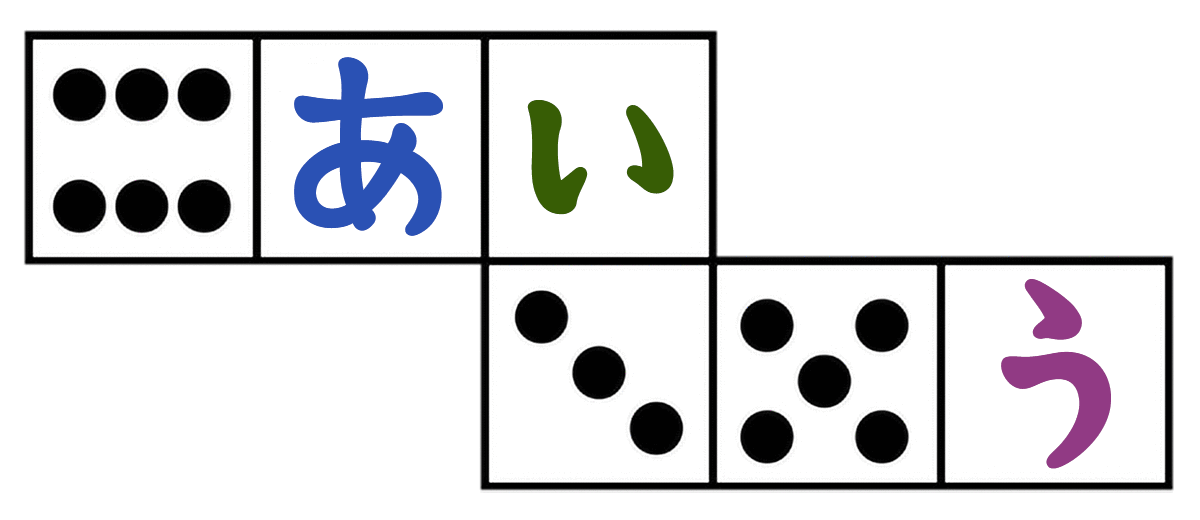
色がぬられてない面積は?
次は、色がぬられていない面積を求めてもらおうではないか~
まずは8個の立方体でやってみよう。
1辺が2cmの立方体8個を下の図のように並べ、表面に水色のペンキをぬりました。色がぬられていない面積は何cm²ですか。
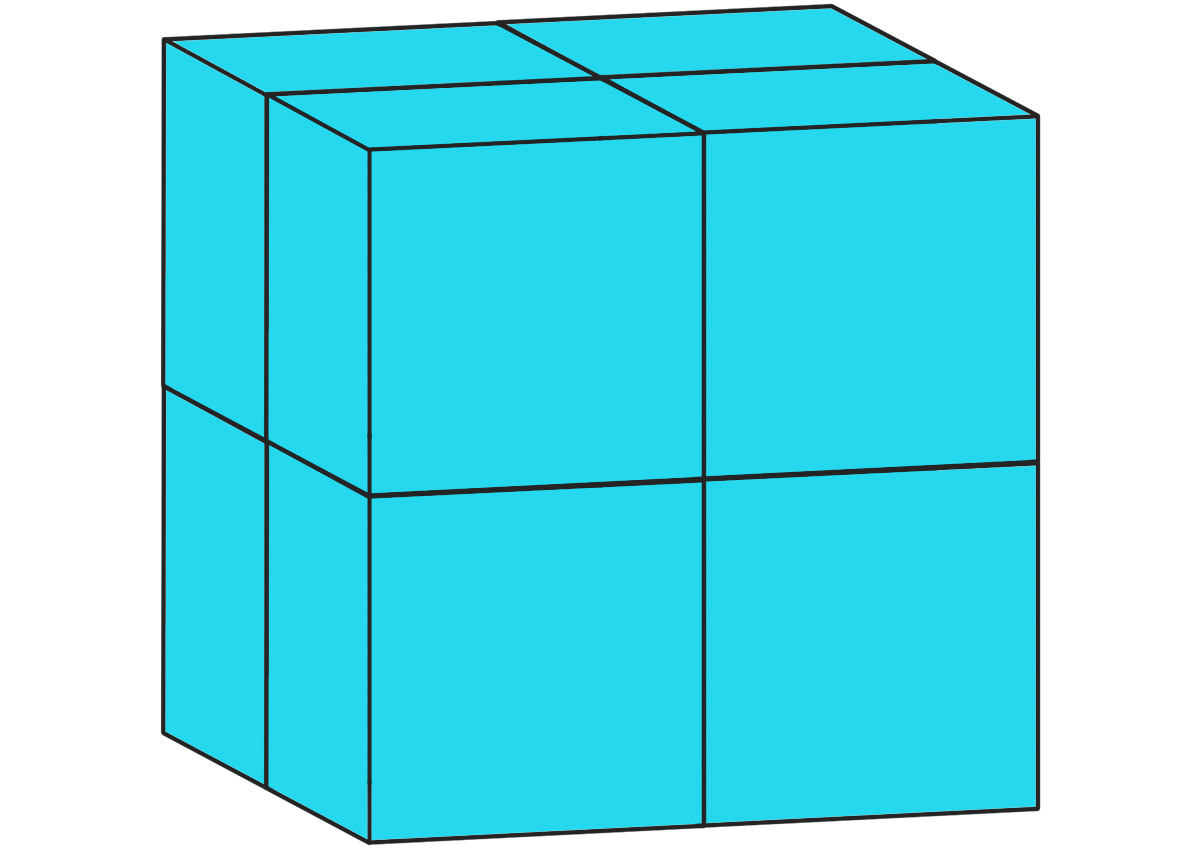
8個くらいなら
いろんな答えの出し方があるよね~
なので、、「こんな考え方もあるか」っていうのを書きますよ。
はい、書きます
1辺が2cmの立方体が8個ある。
それぞれ、色がぬられていない面は3面ずつ。
ということは、
色がぬられている面も3面ずつ。立方体は6面だからね。
なので、
色がぬられている面積と
色がぬられていない面積は
この並べ方の場合
同じ
じゃあ 色がぬられている面積を計算しちゃえ!
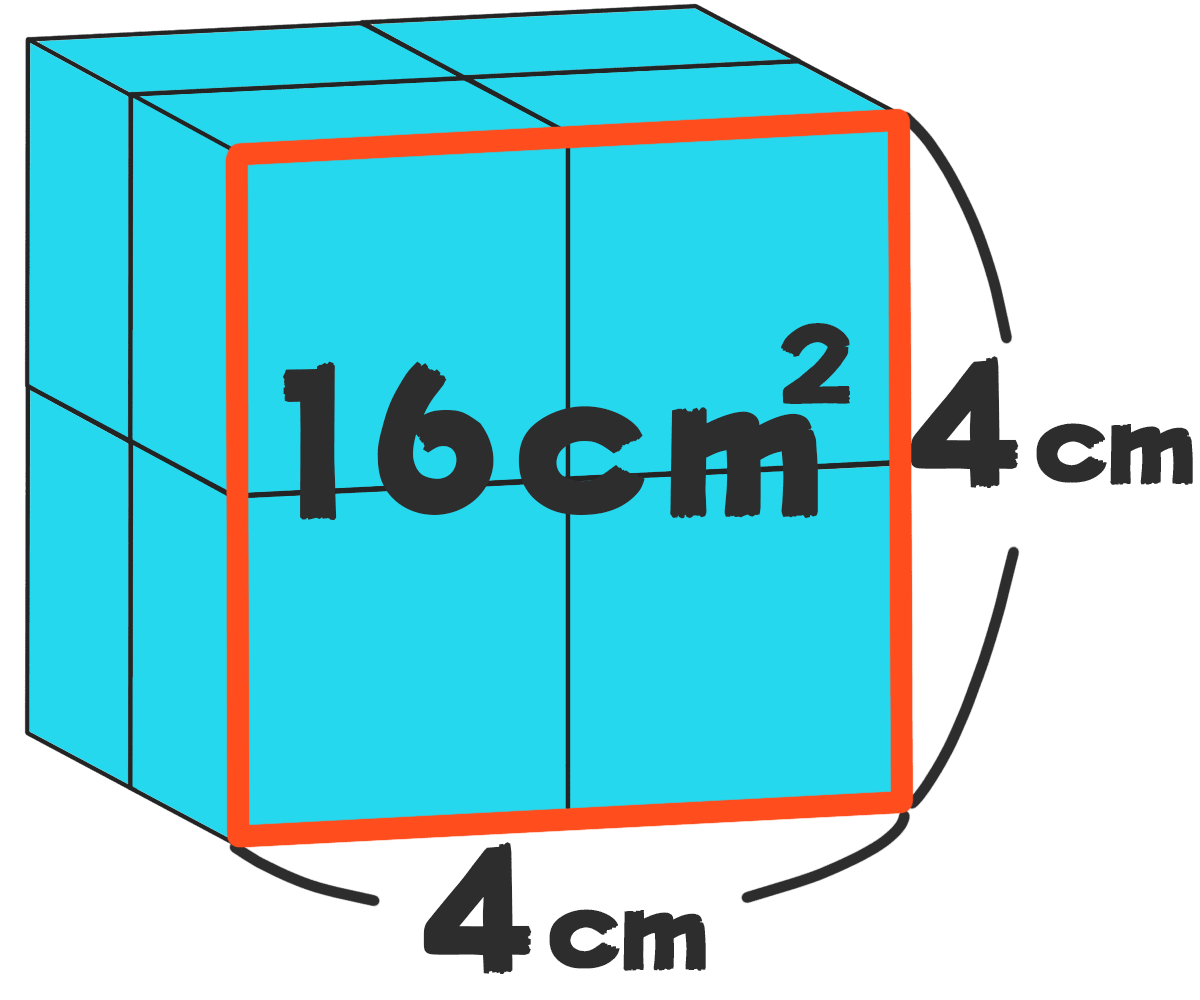
こんな感じで、4×4=16
1つの面は16cm² これが6面あるから
16×6=96
つぎは立方体を増やしちゃう!
1辺が1cmの立方体を たて、横、高さ それぞれ5個ずつ下の図のように並べ、表面にペンキをぬりました。色がぬられていない面積は何cm²ですか。
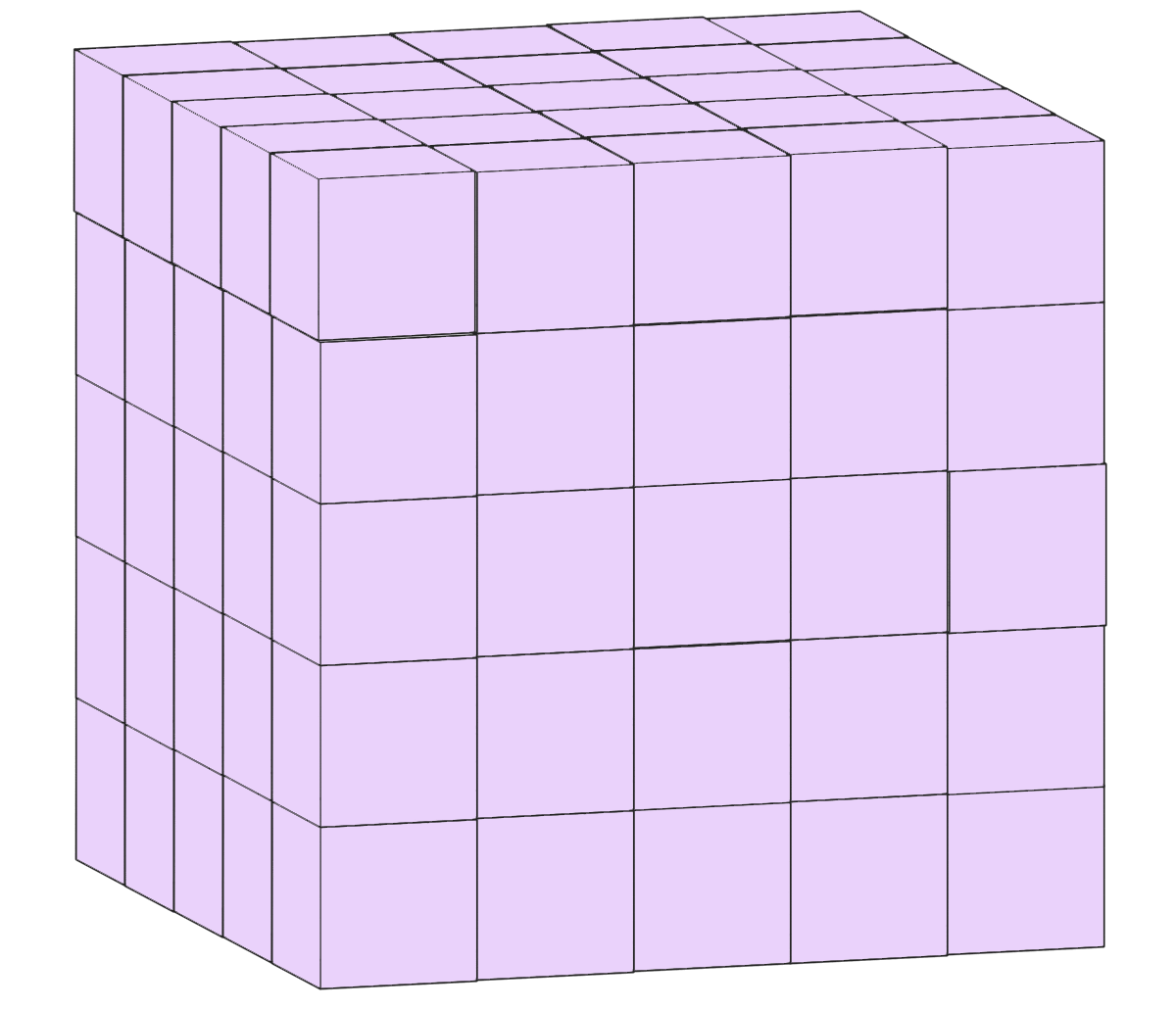
どうやった?
すべての表面積 - ぬってある面積 = ぬられてない面積
ぜんぶの表面積から 色がぬってある面積を引けばいい!
まず、全部の表面積をもとめよ
ブロック1個の表面積は?
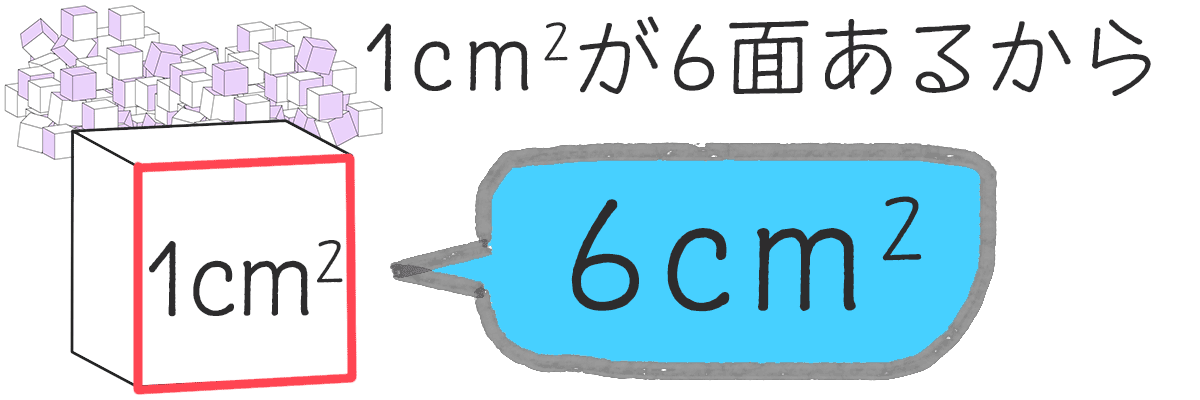
1辺1cmの立方体だから 1つの面の面積は、1×1で1cm²
それが6面あるので6cm²

ブロック1個の表面積は6cm²
はいOK! つぎ!
そのブロック何個ある?
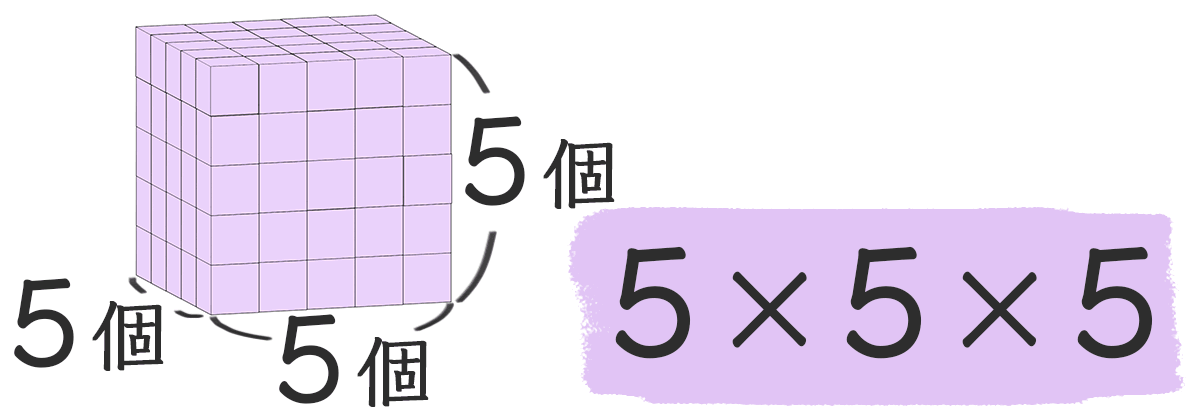
たて5個、横5個、高さ5個 なので、
5×5×5=125

ブロックは125個
6cm²が125個だから?
6×125=750

表面積、ぜんぶ合わせて 750cm²
色がぬってある面積をもとめよ
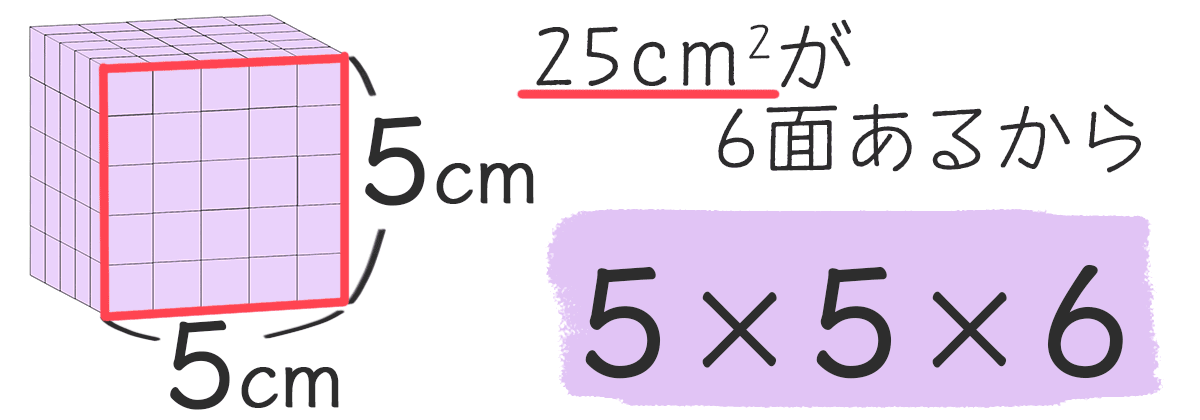
5×5×6=150

色がぬってある面積は、150cm²
答えまとめ
すべての表面積 750cm²から 色がぬってある面積 150cm²を引けば、色がぬられていない面積がわかります!
750-150=600
というわけで答えは、600cm²
3つの面に塗られたブロックを数えて!
立方体のブロックを並べて、表面に色を塗ります。3つの面に色が塗られたブロックは何個ありますか。
- (1)
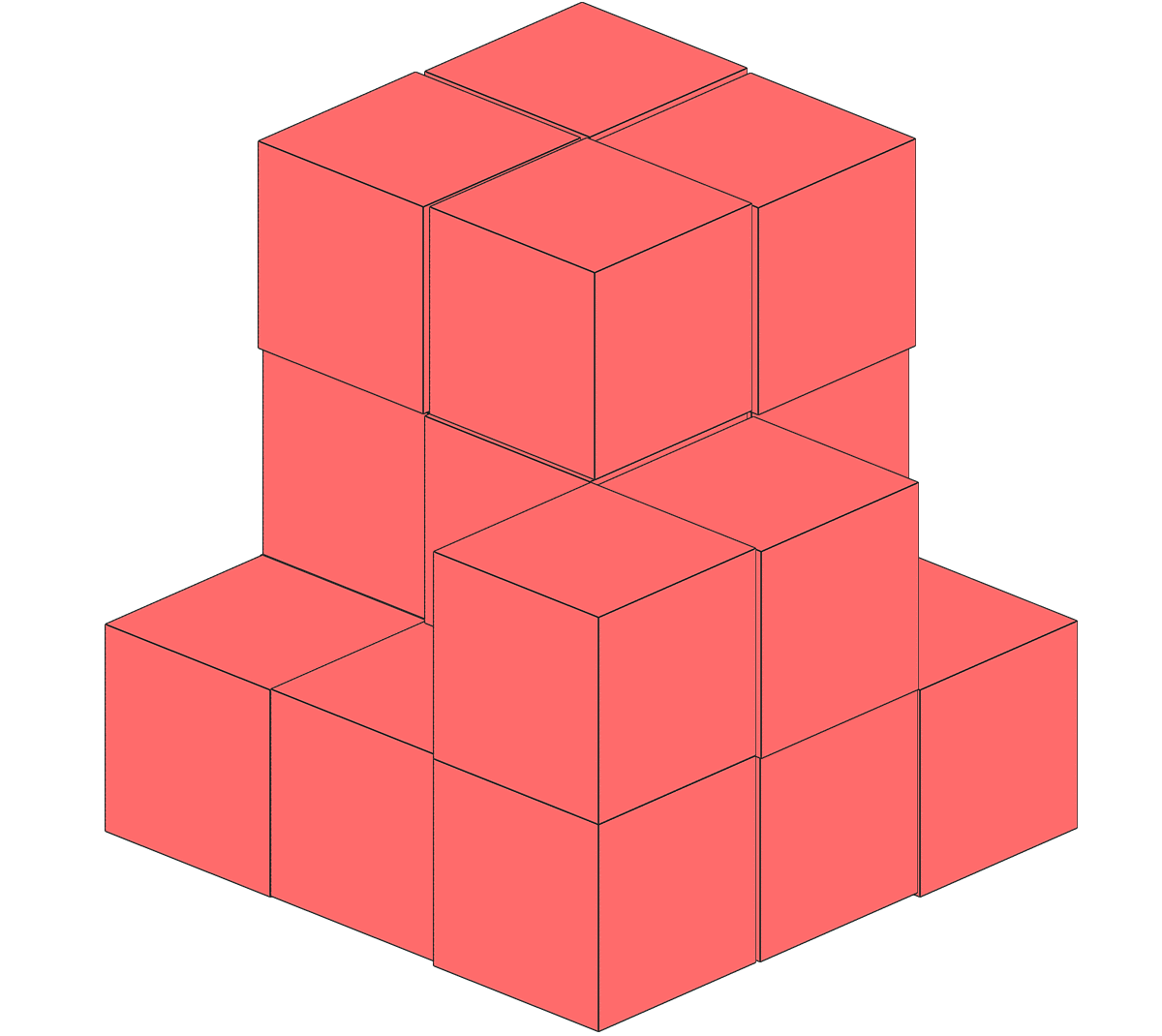
- (2)
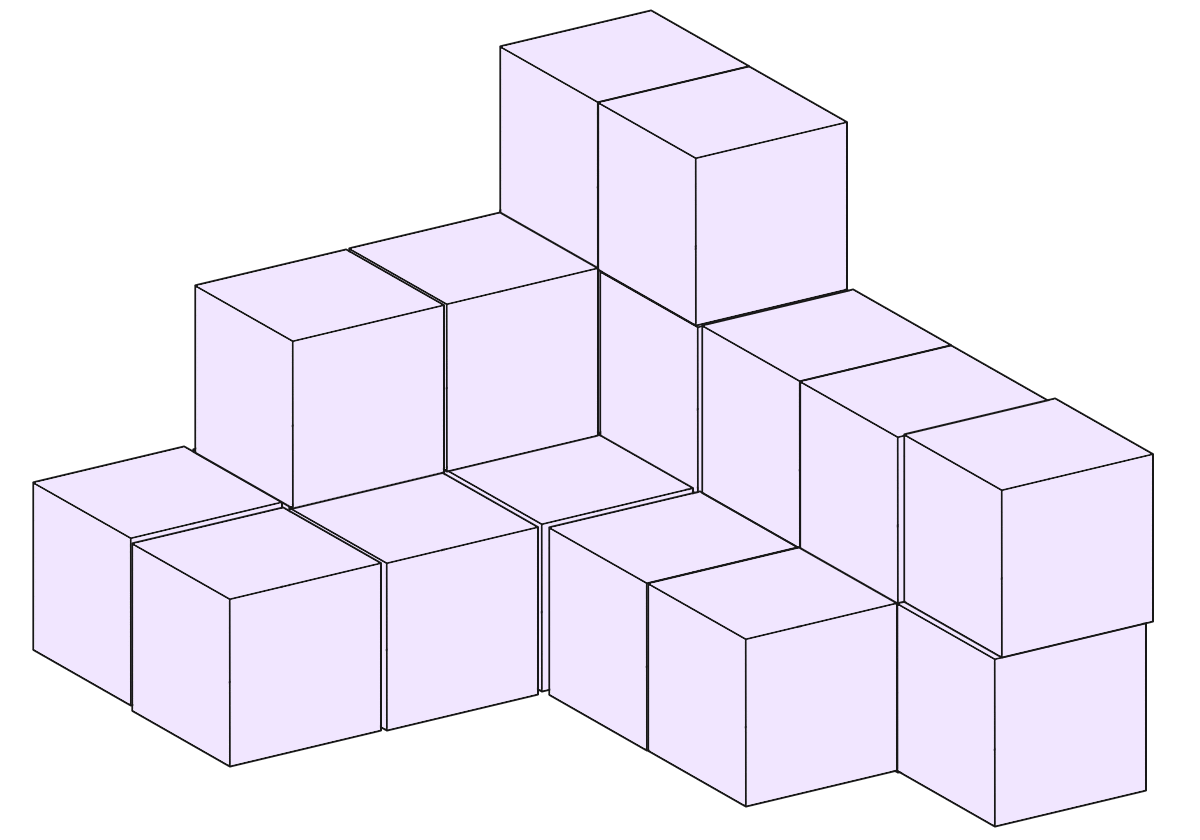
- (3)色つけるの忘れたんで白くぬったと思ってください、、
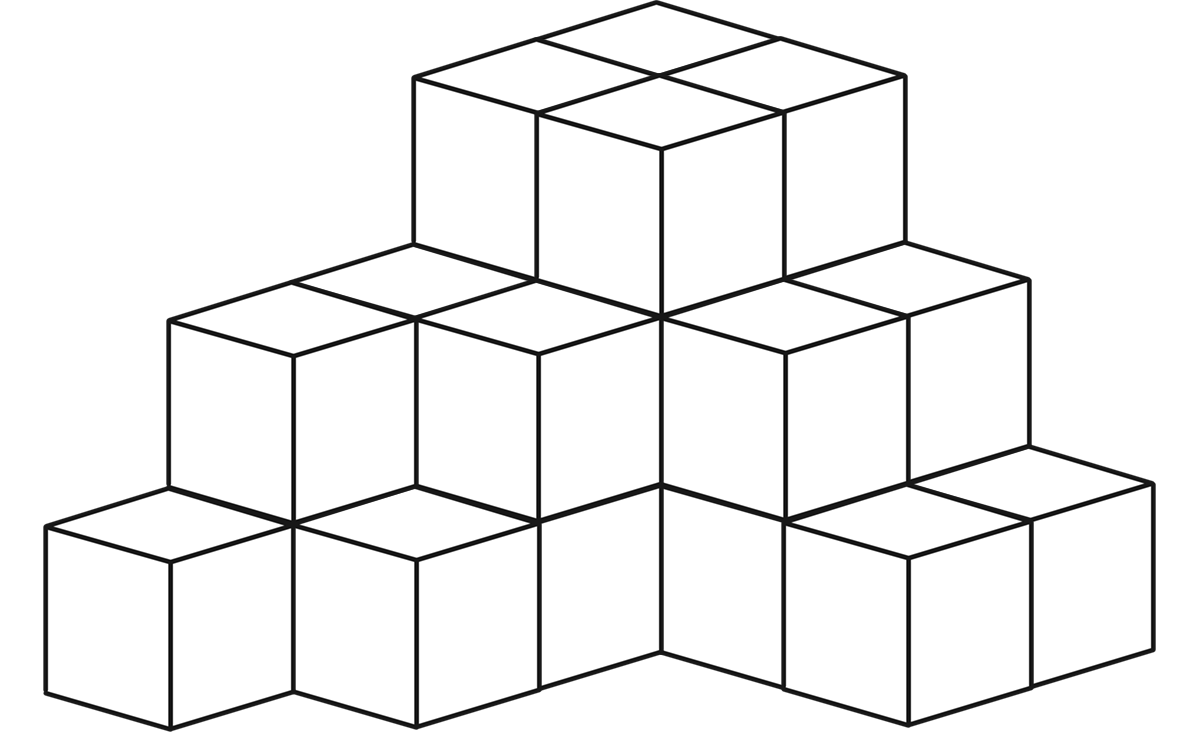
- (4)