角柱と円柱の体積・表面積の問題たっぷり
5年生~6年生
web算数問題集

5年生~6年生におすすめ、角柱と円柱の体積や表面積の問題がいっぱいです。
角柱と円柱の超基本っすねー。っていう問題から、体積とか 表面積の ちょっと難しくない?っていう問題までたくさんやってみましょう。
図で見るくわしい解説もあるよ。
5年生~6年生 って書いたけど別に何年生でもOKです。 「角柱・円柱のこと忘れたー!やべー!」って中学生もカモン
このページでできるようになることは、この3つ
『角柱とは、円柱とは』を知ることができる。
角柱や円柱の体積を求めることができるようになる。
角柱や円柱の表面積を求められるようになる。
面積の求め方を忘れた! そもそもやってない! って人は↓
いざ、出陣~
角柱と円柱を知ってるかチャレンジ!
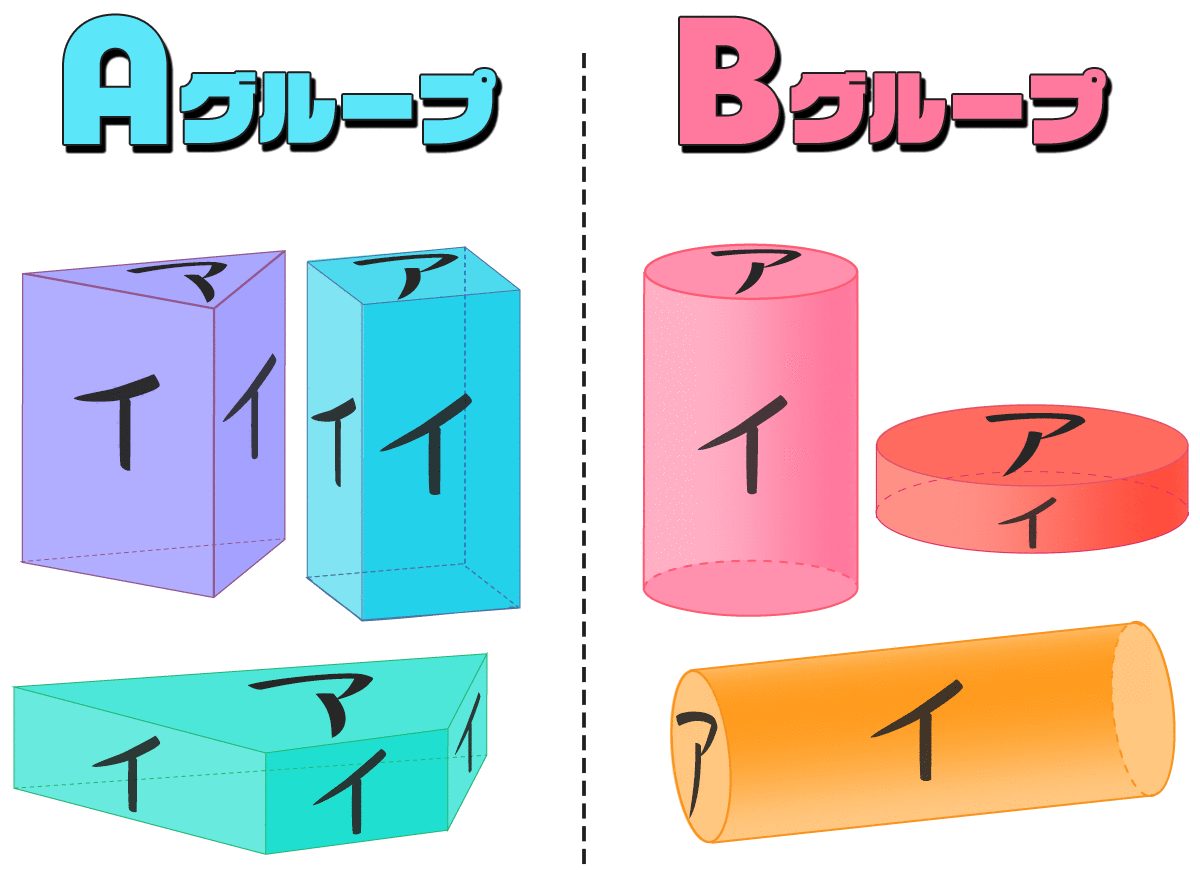
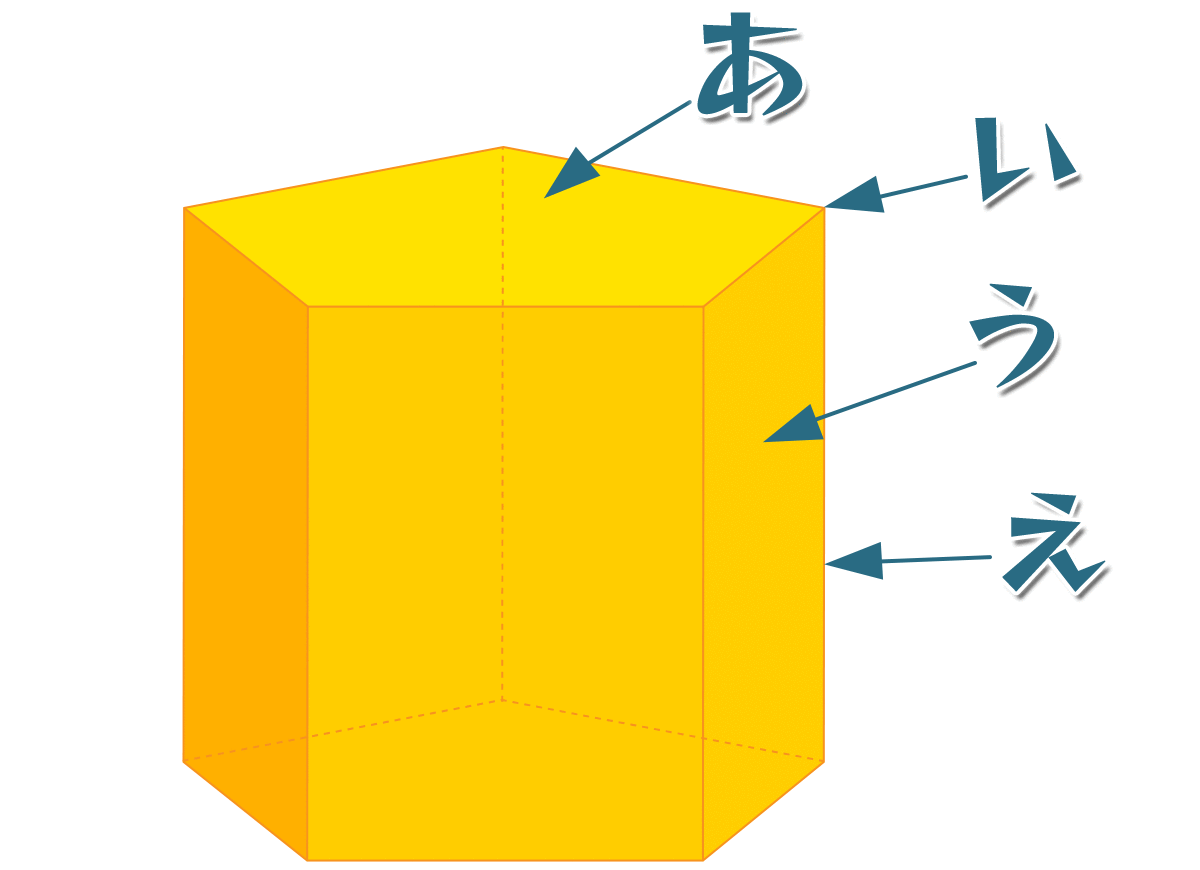
下の図の角柱について答えてもらう。(あ)~(え)は何でしょう。
下の図のような円柱についてお答えください。
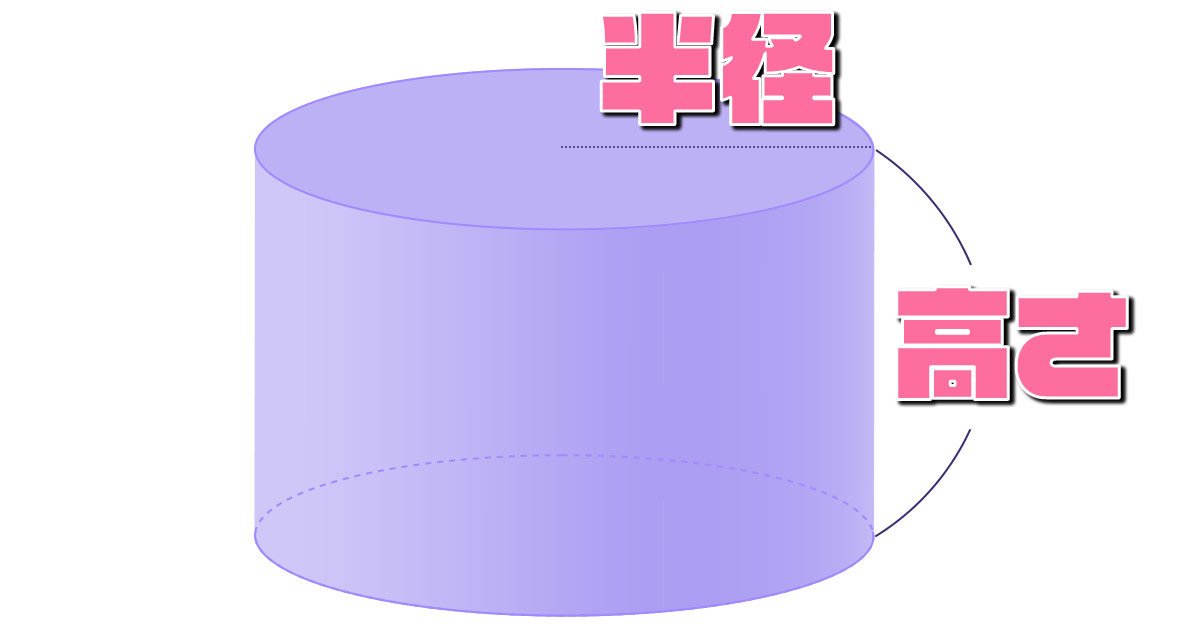
円柱の底面の半径が2cm、高さが10cmのとき 側面の面積は何cm²ですか。
(3)の 答えと解き方
答え:125.6cm²
底面の半径2cm、高さ10cmの円柱を~ 展開図でドン!
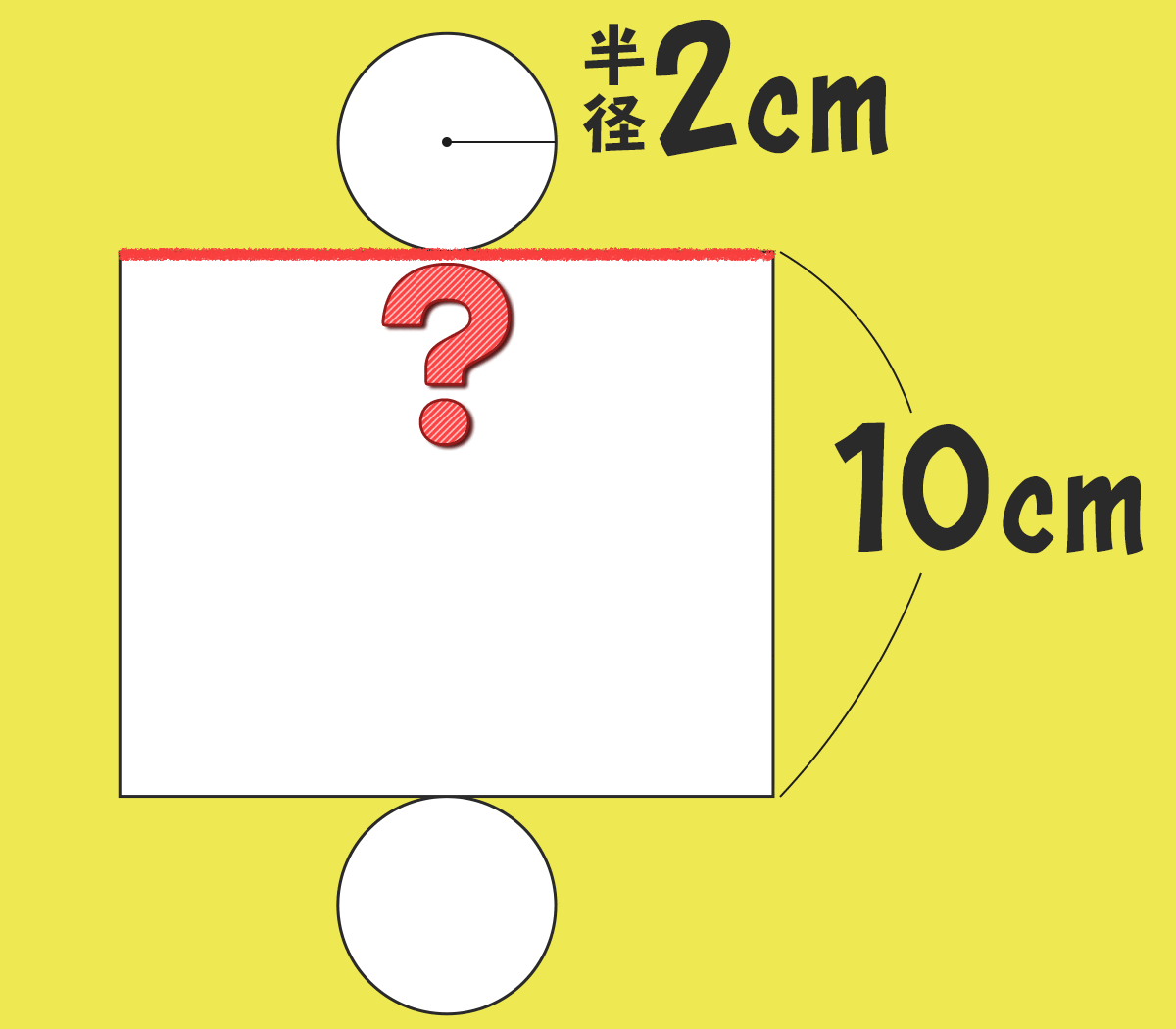
側面は長方形だから 「たて×横」 で面積を出すことができる。
たて(高さ)は10cmなので、横の長さが分かれば・・いける!
底面の円周を計算
側面の面積 → たて×横

円柱は、底面の円周と 側面の横の長さがいっしょ。ってことを使って答えを出す!でした
角柱と円柱の表面積
角柱・円柱の表面積の問題をやってみよう! 角柱・円柱の体積はこのあとやります。これで表面積の求め方もバッチリ~
下の文章は角柱と円柱の表面積の求め方について書かれてる。□に入る数字は何?
三角柱の表面積を求めよう。
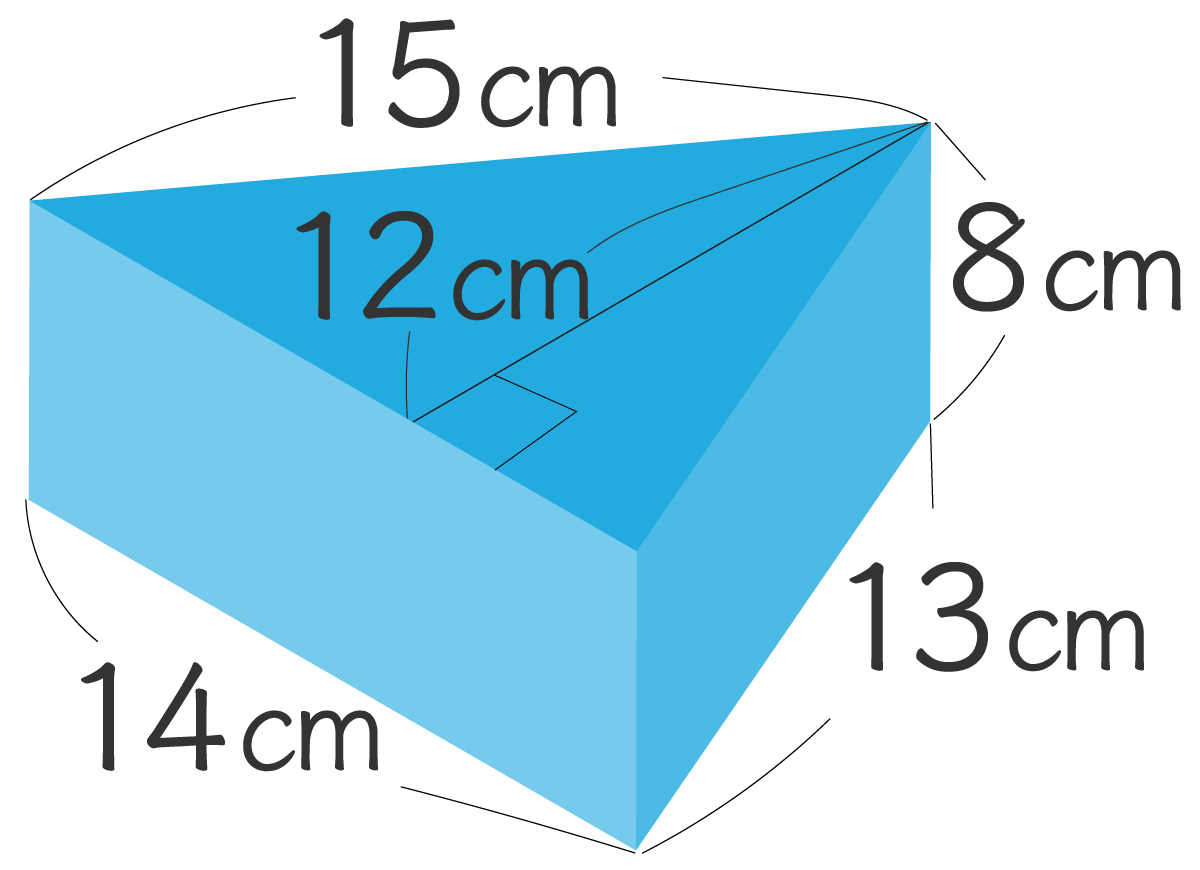
解き方
この三角柱の展開図はこんな感じ~
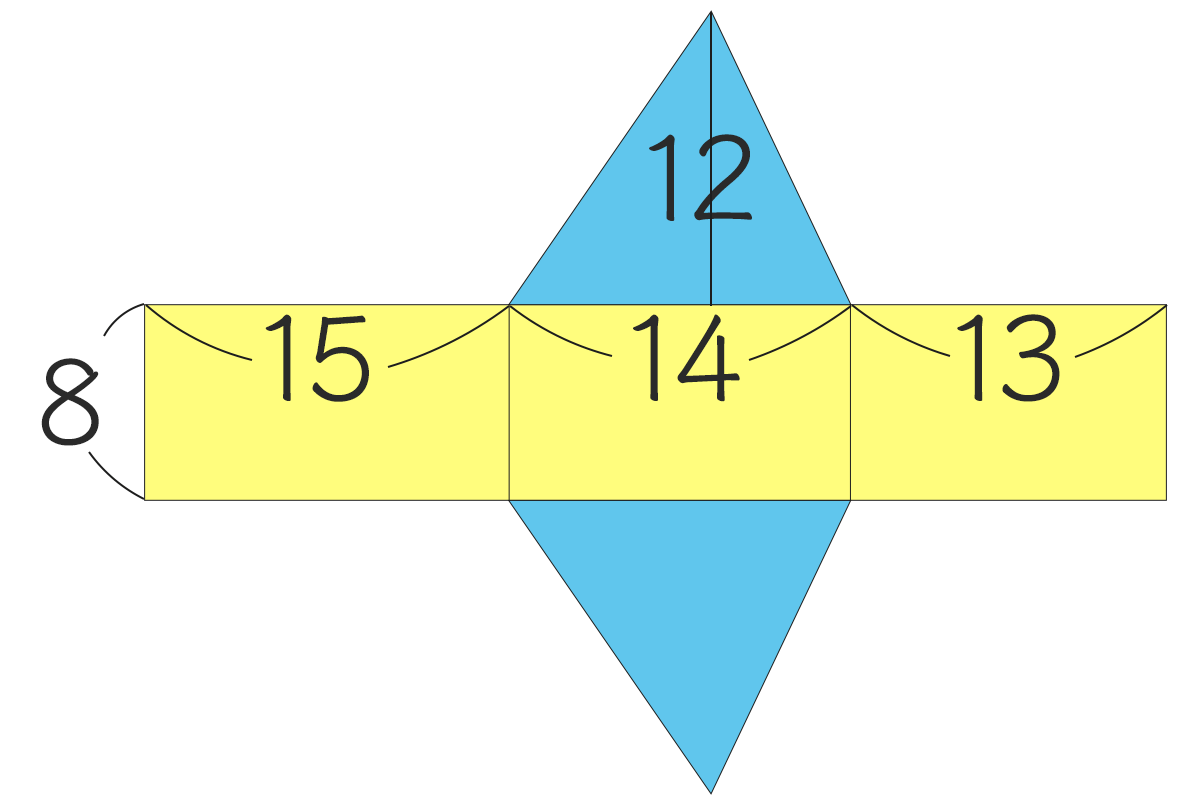
底面の三角形2つと 側面の長方形、それぞれの面積を足せばよい。
三角形の底面の面積を 2倍
側面の長方形の面積
底面積と側面積を足して完了!

側面は、横の長さ(13cm、14cm、15cm)を全部足してから 8をかけてみた
側面を3つに分ける考え方でやってみます
8×13=104
8×14=112
8×15=120
104+112+120=336
こっちより計算が楽じゃない? 楽だよね、どうだろ、いやきっと楽よね。だよね
底面の半径6cm、高さ7cmの円柱の表面積を求めよう。
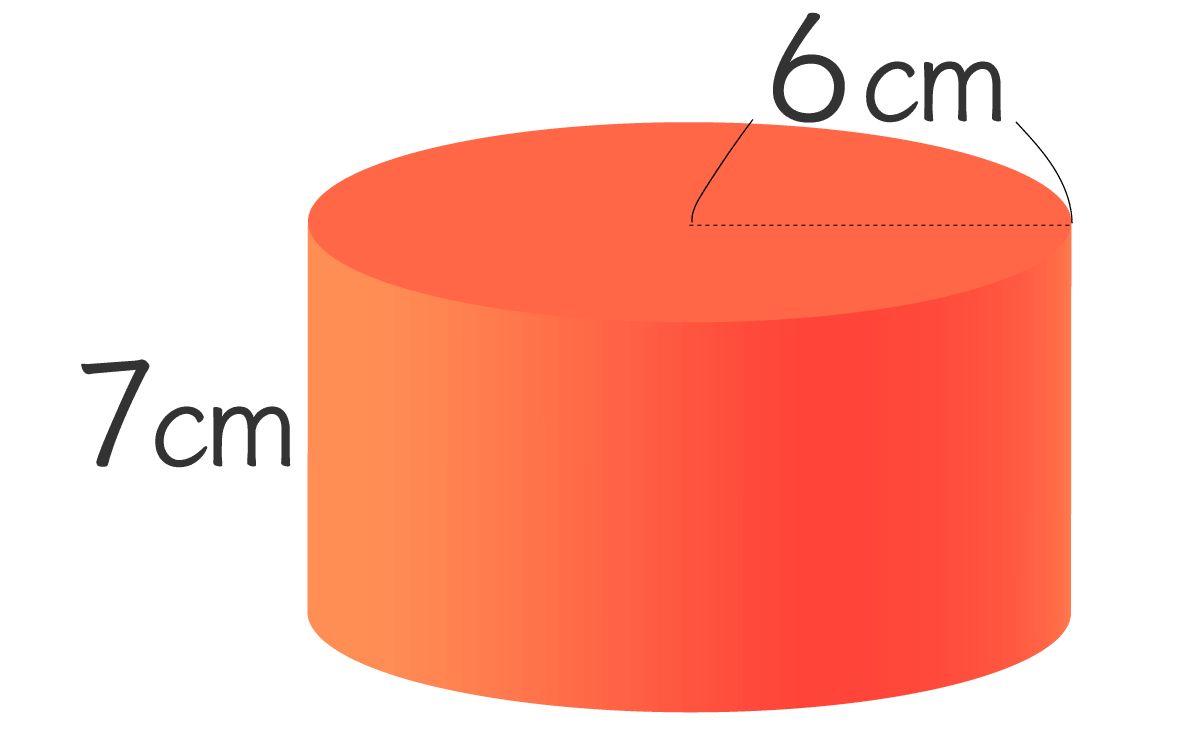
解き方
円柱を展開図にします
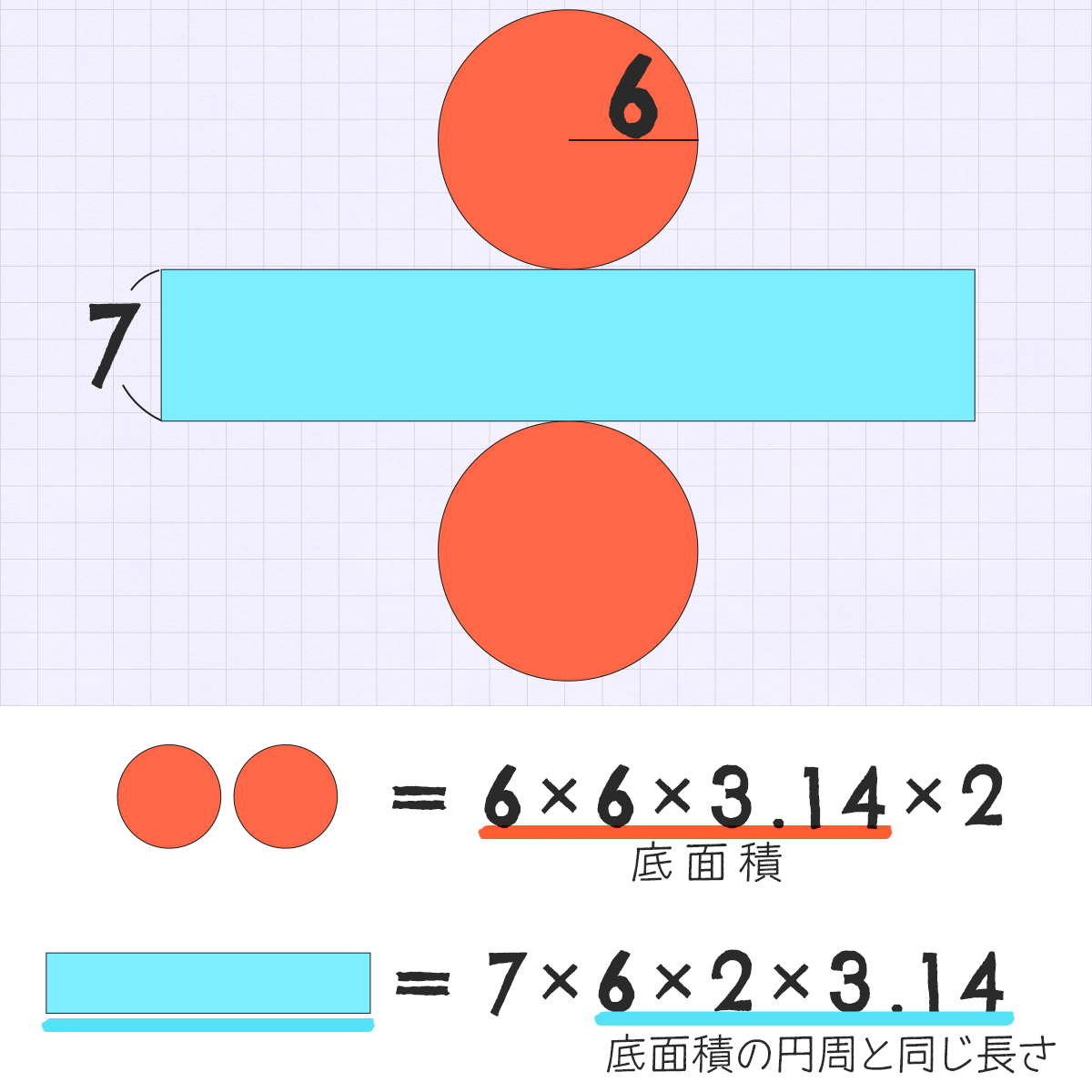
底面の円が2つと 側面の長方形、それぞれの面積を出しましょ。
底面の円を計算
底面の面積を2倍・・・これを式にしてみる
側面の長方形
長方形の面積は、「たて×横」 だよね。
たて7cm、横は底面の円周と同じ なので、これを 「たて×横」 に当てはめてみる。
底面積と側面積を足して完了!
円柱から$ \dfrac{1}{4} $を切り取った立体がある。半径と高さがつぎの長さのとき、この立体の表面積はいくつか求めるのだ。

1問目だけでもイイです。解説を見てもっと解く練習をしたければ2~4問目をやる!とかね
- 半径2cm 、高さ4cm
- 半径1cm 、高さ5cm
- 半径5cm 、高さ10cm
- 半径10cm 、高さ20cm
答え見るとするか
- 答え 72.52cm²
- 答え 38.26cm²
- 答え 453.25cm²
- 答え 1813cm²
1問目で解説しま・・? !!!

はい、にげる押さない。
では、底面の面積からやっつけます
底面積
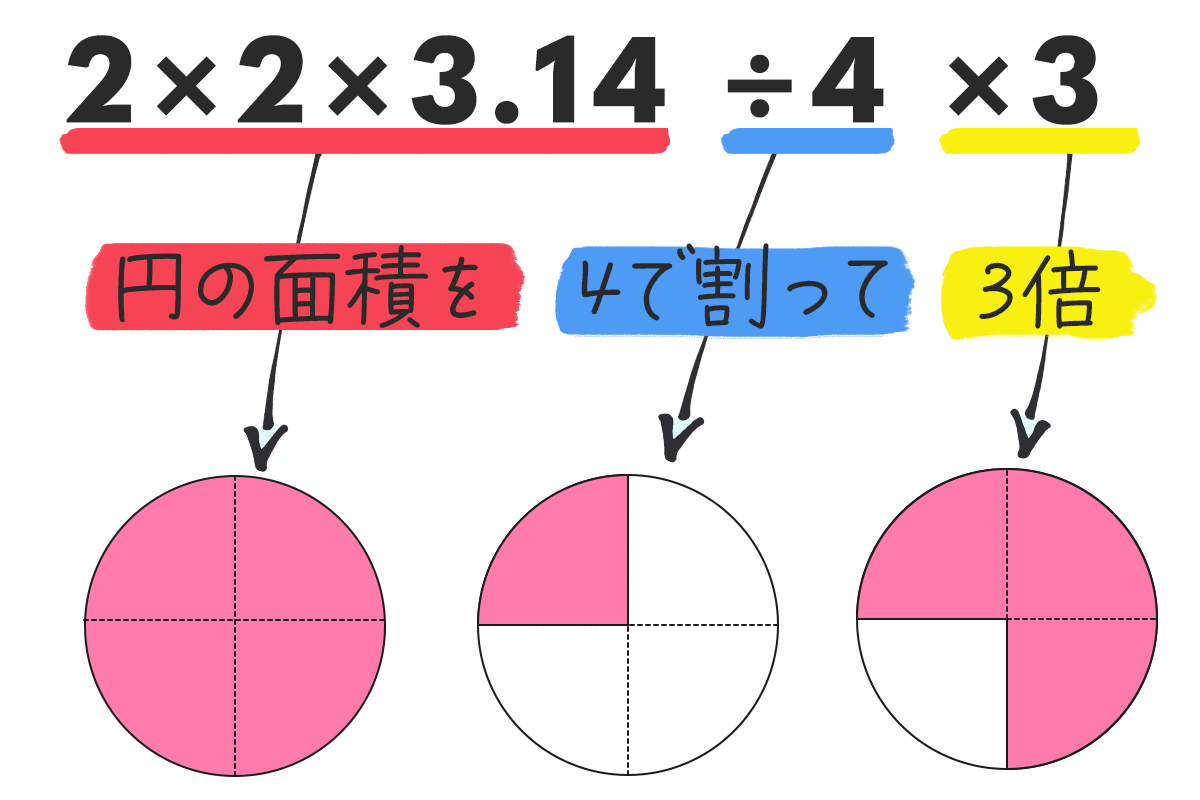
円の面積を4で割れば、$ \dfrac{1}{4} $の面積が出る。 で、それを3倍する。
これで ひとつの底面はOK!
底面は2つあるから、さらに2倍するよ~ まとめると~
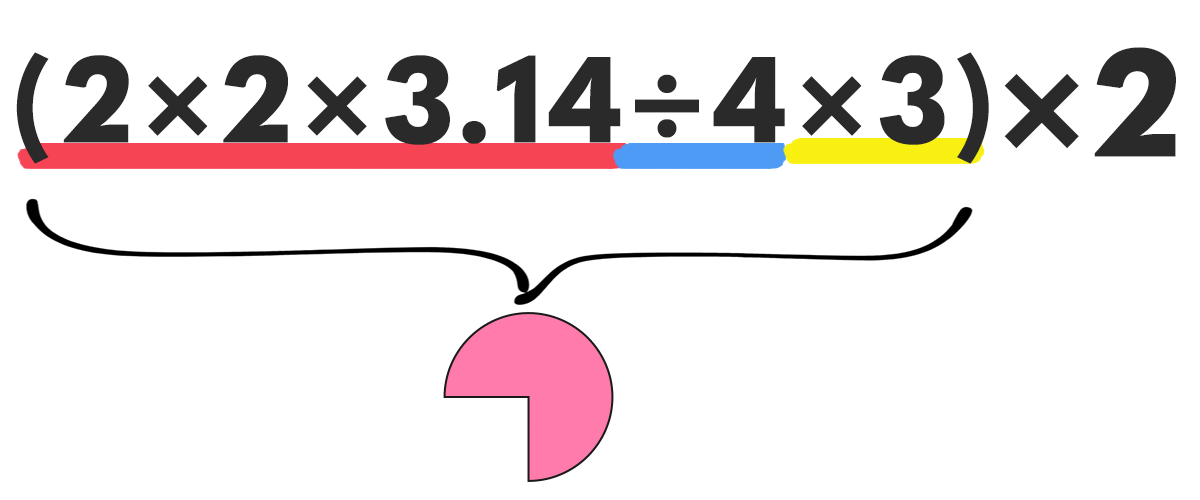
ちょっと計算してみる
\begin{eqnarray} (2 \times 2 \times 3.14 \div 4 \times 3) \times 2 &=& \\[0.5em] 9.42 \times 2 &=& 18.84 \\ \end{eqnarray}
底面積2つで 18.84cm²
これで2つの底面の面積(底面積)はできた。つぎは側面積!
側面積
下の図は底面を外したので、側面だけ。 切りとり線で切って 開くとどんな形でしょうか。

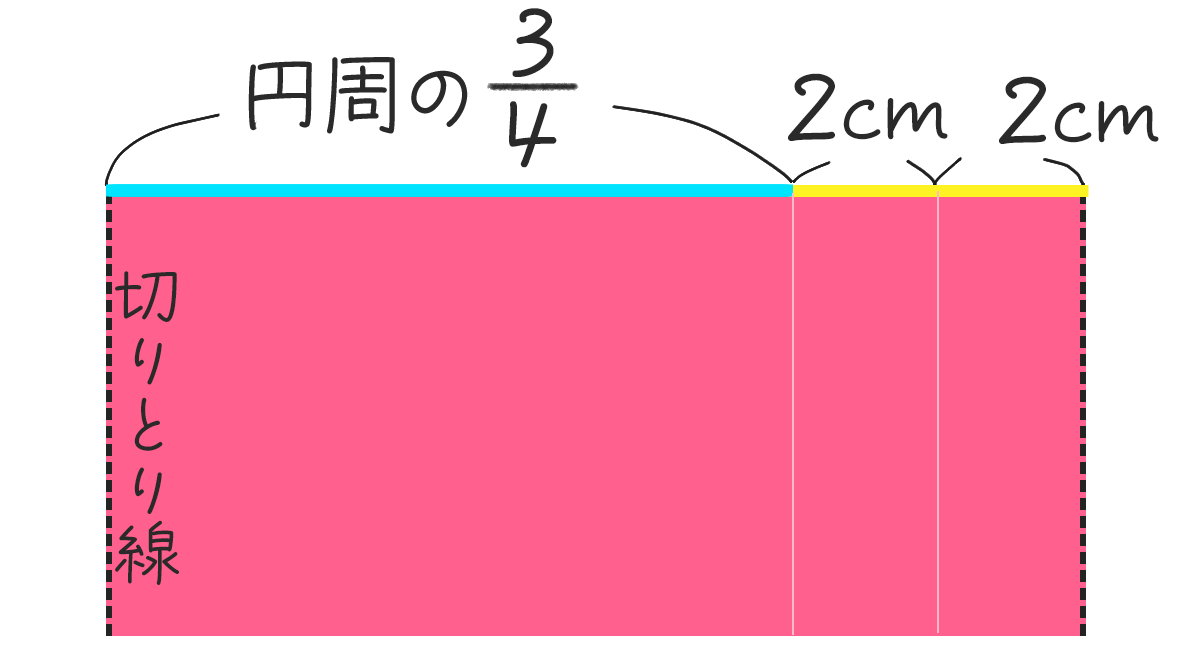
ただの長方形。
たて4cm、 横は ( 円周の$ \dfrac{3}{4} $ + 2 + 2 )
長方形の面積は たて×横 だから、
4×( 円周の$ \dfrac{3}{4} $ + 2 + 2 )=
これを当てはめると
ヒント「 円周を 4で割って 3倍 」
これで側面積もOK!
ちょっと計算してみる
\begin{eqnarray} 4 \times ( 2 \times 2 \times 3.14 \div 4 \times 3+2+2) &=& \\[0.5em] 4 \times ( 9.42+2+2) &=& \\[0.5em] 4 \times 13.42 &=& 53.68 \end{eqnarray}
側面積は 53.68cm²
底面積 + 側面積
18.84 + 53.68 =72.52

というわけで、1問目は72.52cm² !!
できた!
角柱と円柱の体積の問題
つぎは角柱・円柱の体積の問題です!
角柱と円柱の体積の求め方は知ってる?
角柱でもある 直方体や立方体の体積は 前にやっているはず~ おぼえてるかい
角柱と円柱の体積の求め方について、□に入る言葉は何?
角柱と円柱の体積を求める練習問題!すでに底面積が分かってるから かけ算をするだけという超かんたんな問題~
- 底面積が20cm² 、高さが6cmの三角柱の体積を求めよ。
- 底面積が35cm² 、高さが9cmの四角柱の体積を求めよ。
- 底面積が50.24cm² 、高さが10cmの円柱の体積を求めよ。
答え合わせ
- 答え 120cm³20×6=120
- 答え 315cm³35×9=315
- 答え 502.4cm³50.24×10=502.4

角柱や円柱の体積は、「 底面積×高さ 」 で求める~
角柱・円柱の体積を求めよ!まずは超基本の5問
角柱や円柱の体積を求めるのだ。
- (1)
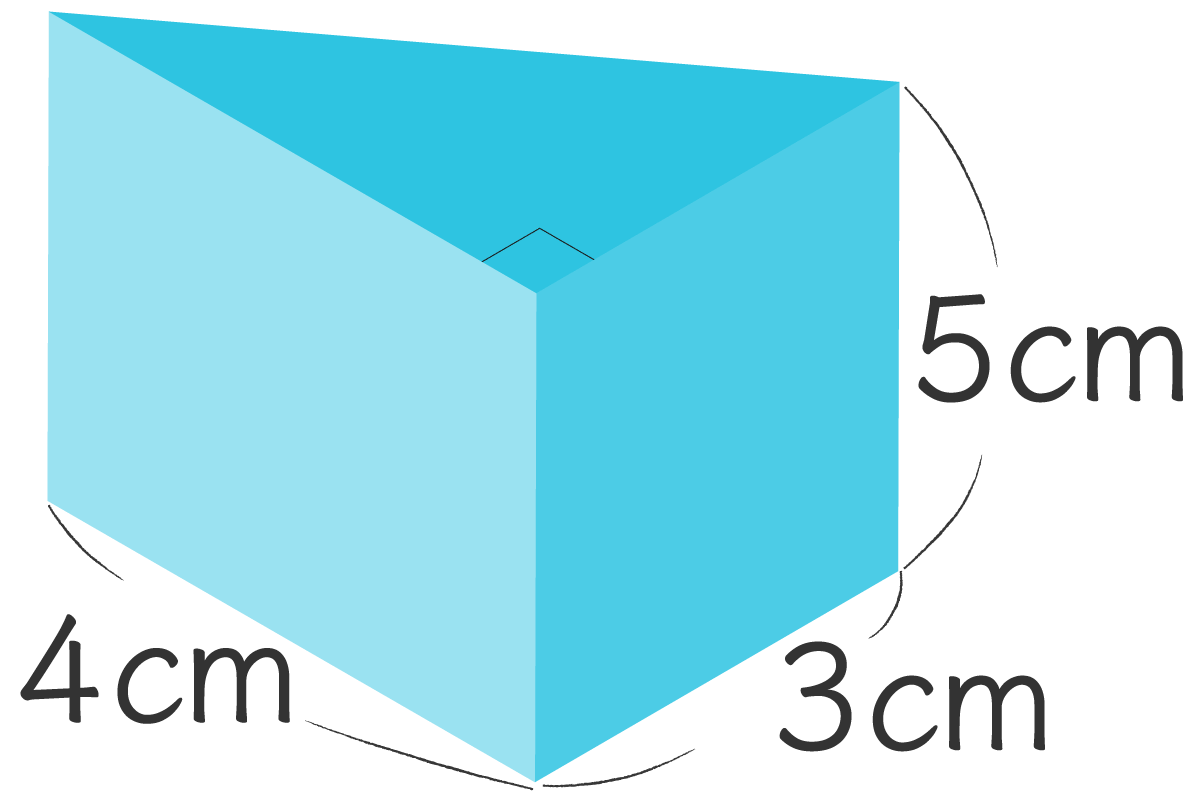
- (2)
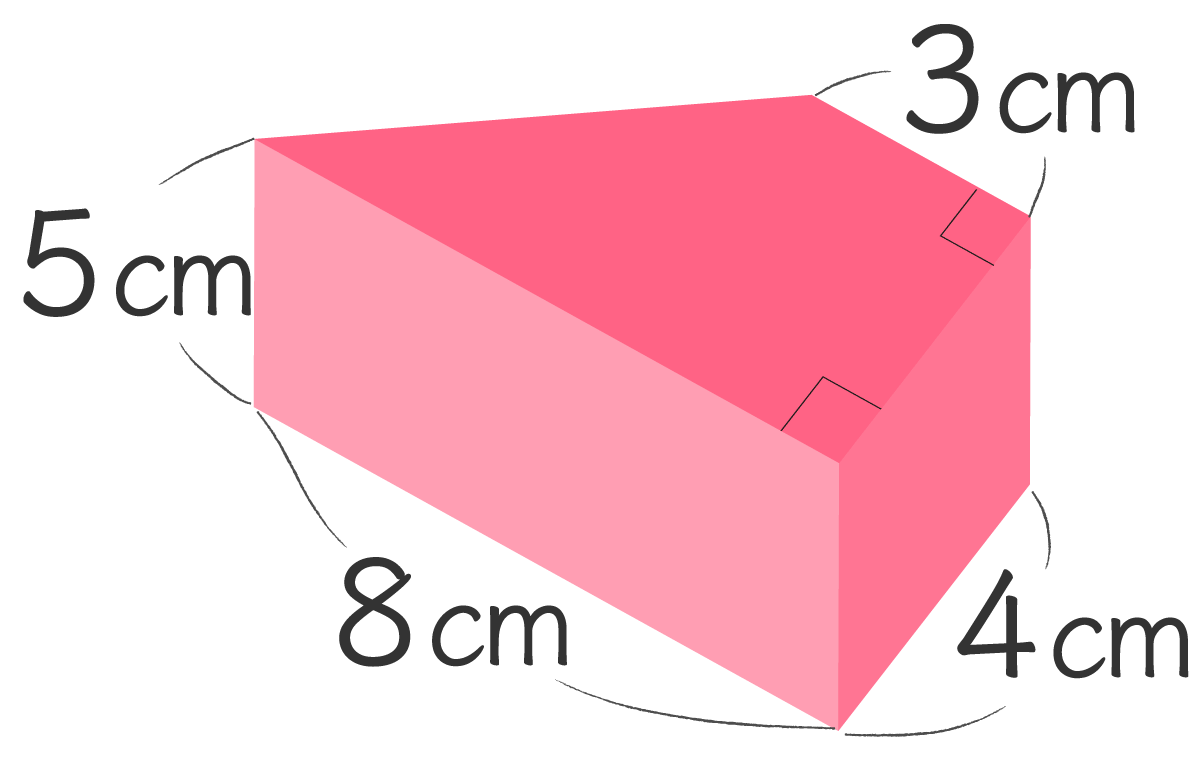
- (3)
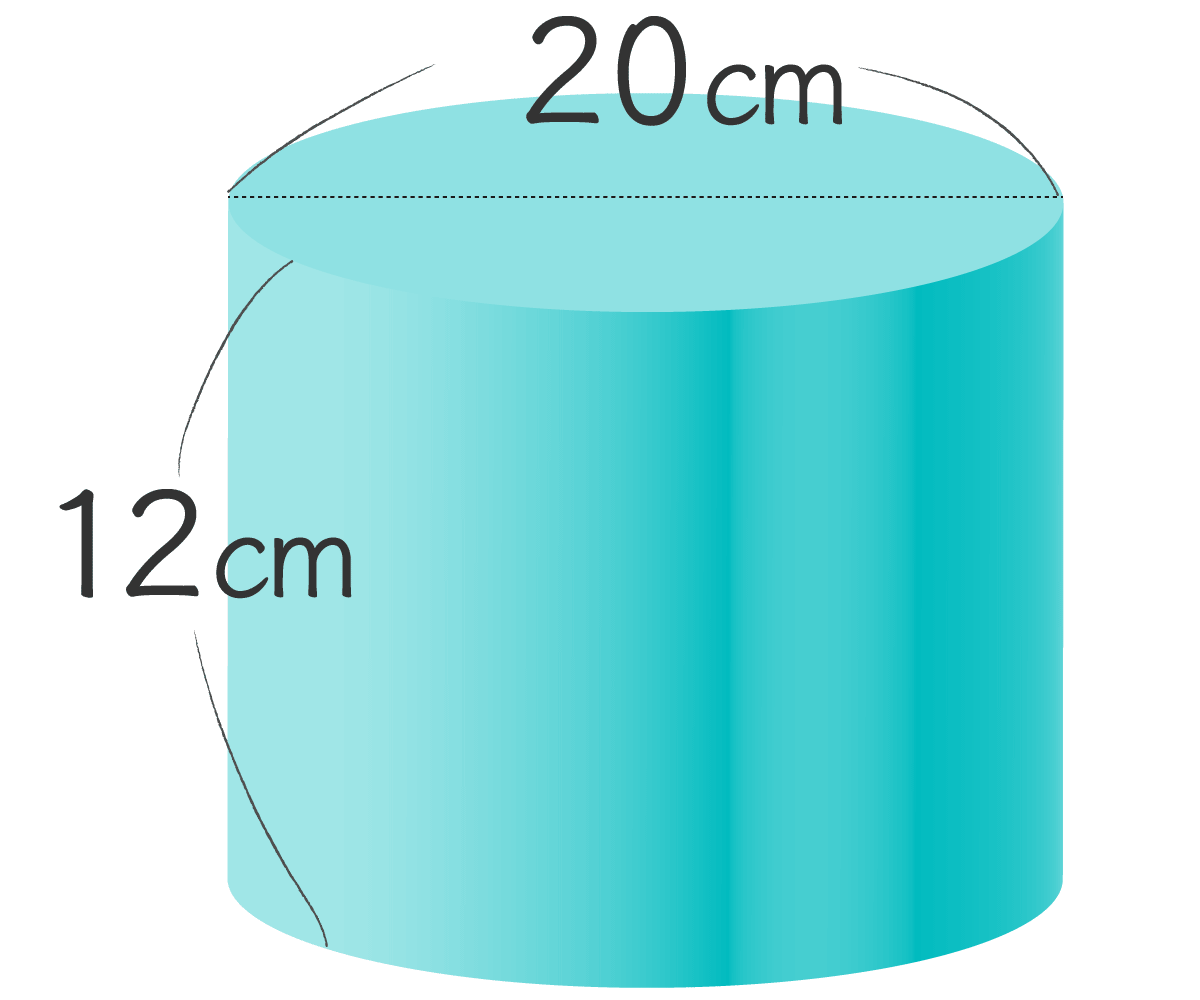
- (4)
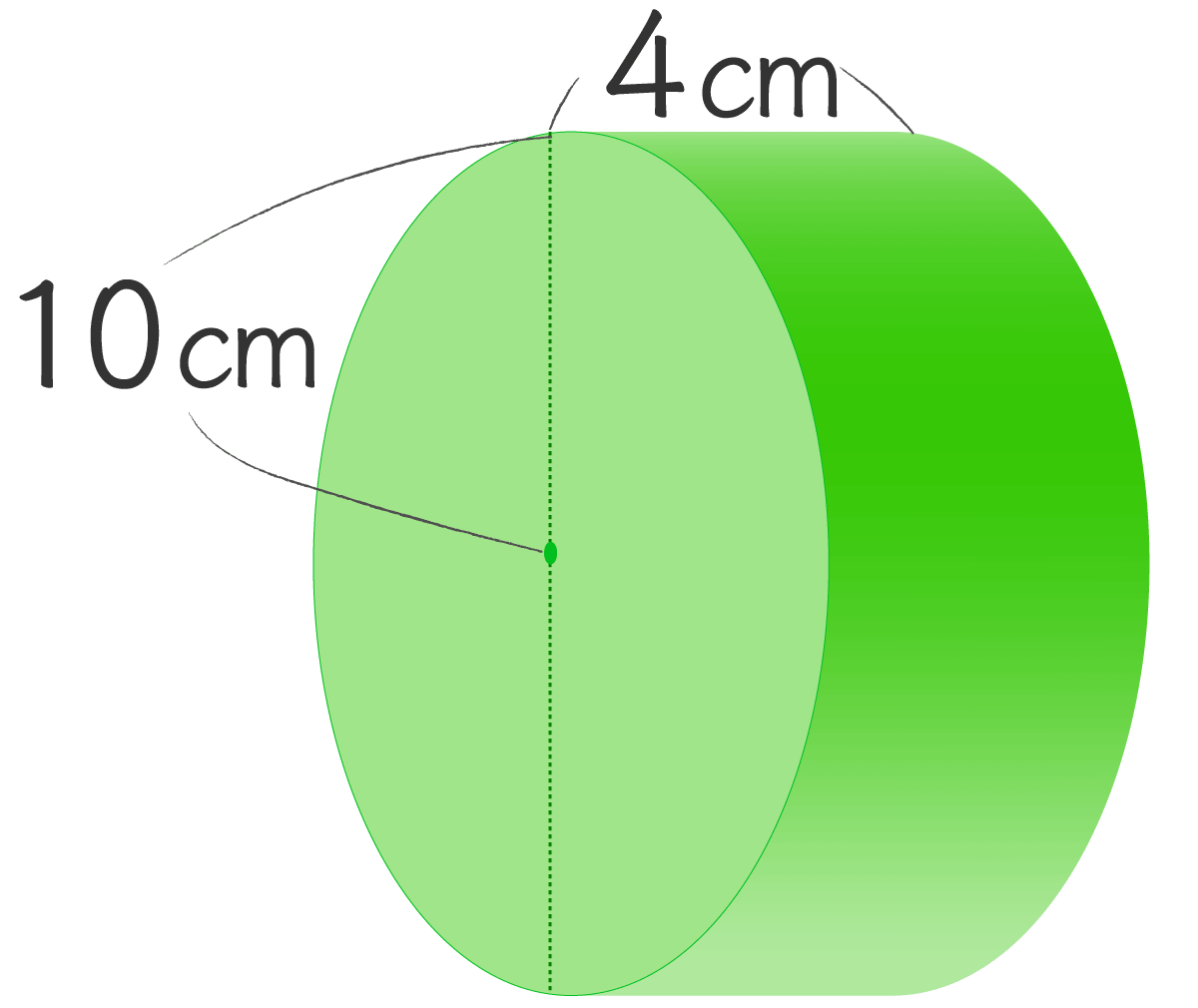
- (5)
レベルアップ!徹底的に角柱・円柱
角柱と円柱のレベルアップ問題をバシバシやってみましょう! どうやって答えを出すか解説もあるよ~色んな問題があるから楽しんでやってみてね~
円柱を半分に切った立体があります。この立体の体積と表面積を求めよ! 半径や直径、高さはつぎの長さとする。
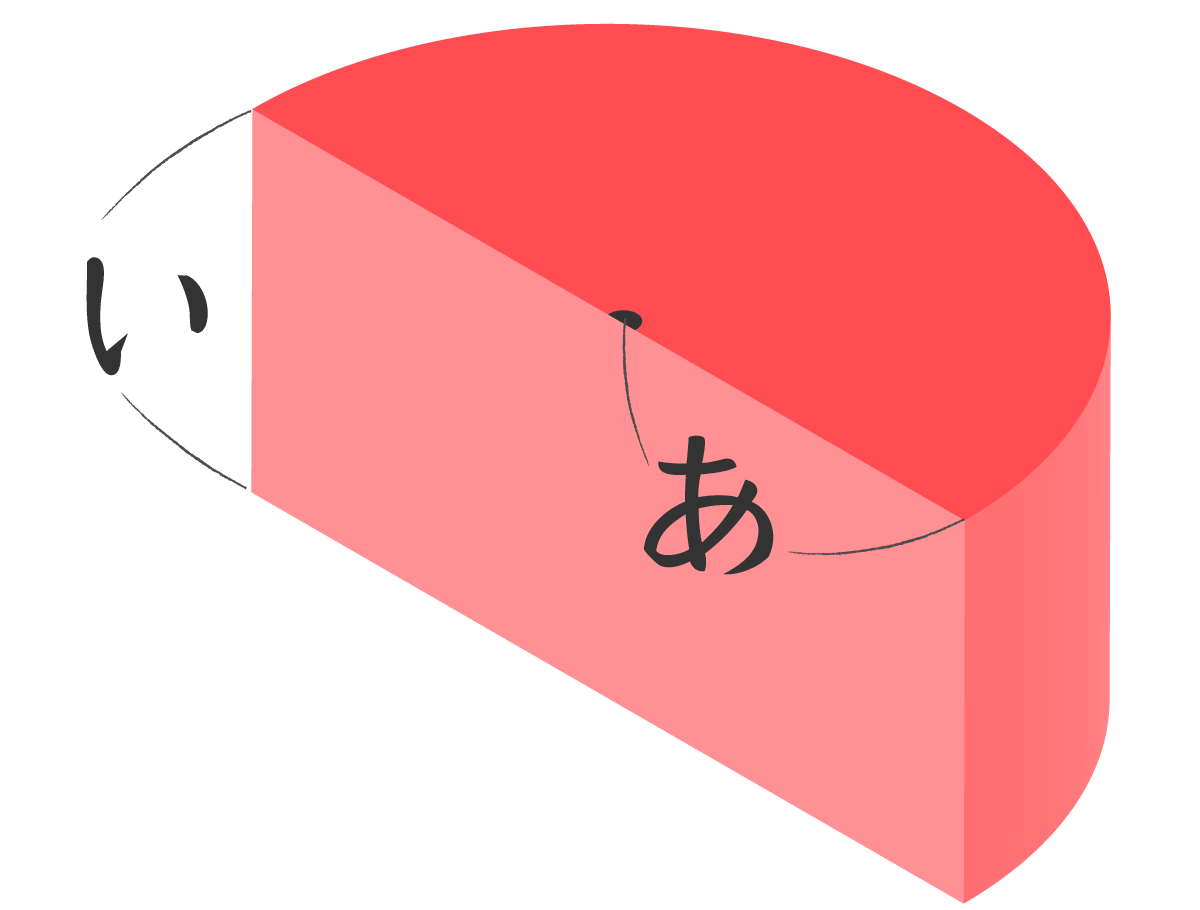
- 半径4cm 、高さ8cmの場合
- 半径10cm 、高さ4cmの場合
- 直径6cm 、高さ10cmの場合
答え & 解説
- 体積 200.96cm³表面積 214.72cm²
- 体積 628cm³表面積 519.6cm²
- 体積 141.3cm³表面積 182.46cm²
1問目をやってみる ~ 体積
半径4cm 高さ8cm
体積は 底面積×高さ
底面である 半円の面積は?
円の面積を半分、 2で割るっつーことですね。
底面積 × 高さ= 体積
はい、できました! これをサクッとまとめちゃうと
4×4×3.14÷2 ×8=200.96
表面積の解説
半径4cm 高さ8cm
展開図カモン!

ぞうさん? いいえ、ちがいます。
では、「底面積 + 側面積」 でいきましょか
まずは底面積の計算!
底面は半円です。半円を2つ合わせたら円ですね。ただの円
底面積
OK~!
つぎは側面積。側面は長方形なので 「たて×横」
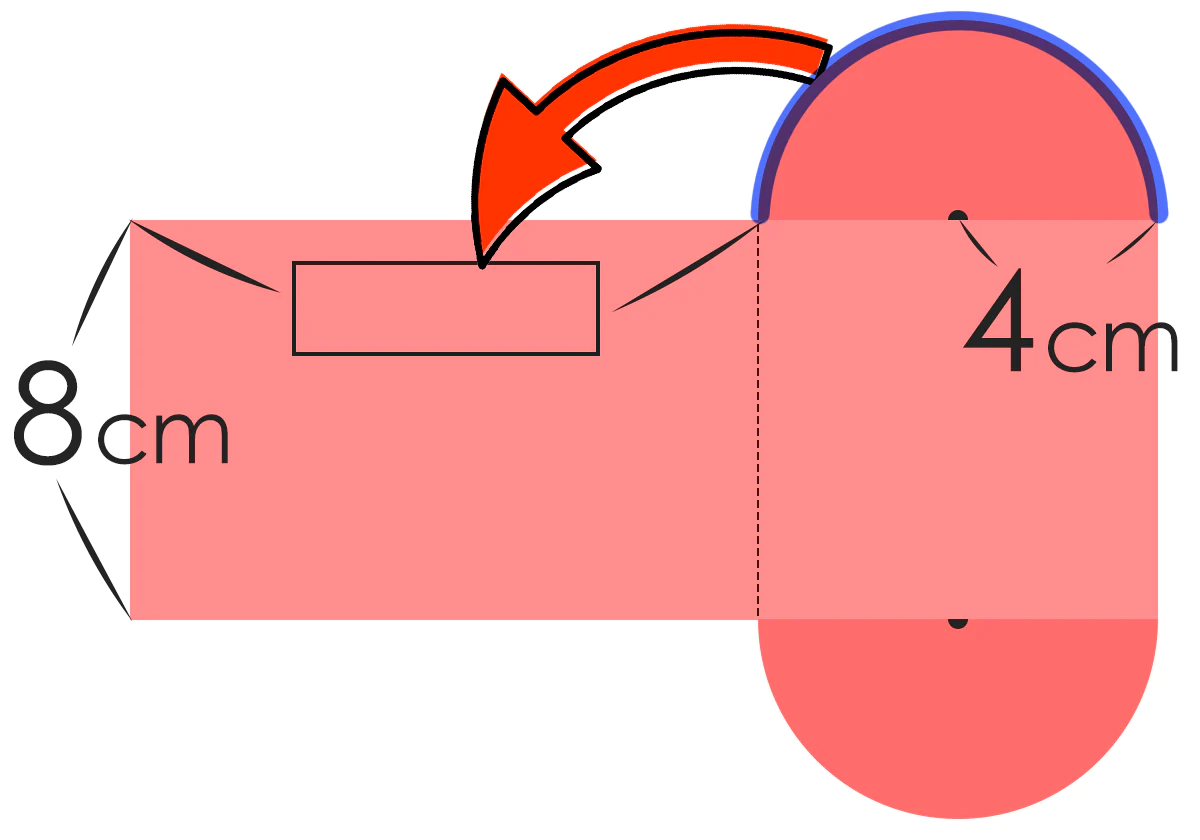
側面積 カッコの中が横の長さだ↓
底面積+側面積=表面積
でした!
底面の直径が20mの円柱から切り取られた立体がある。この立体の高さは7m、底面は中心角が90°のおうぎ形だ。この立体の体積を求めよ。

答え & 解説
答え 549.5m³
10×10×3.14÷4 ×7=549.5
おうぎ形の底面積 × 高さ =549.5
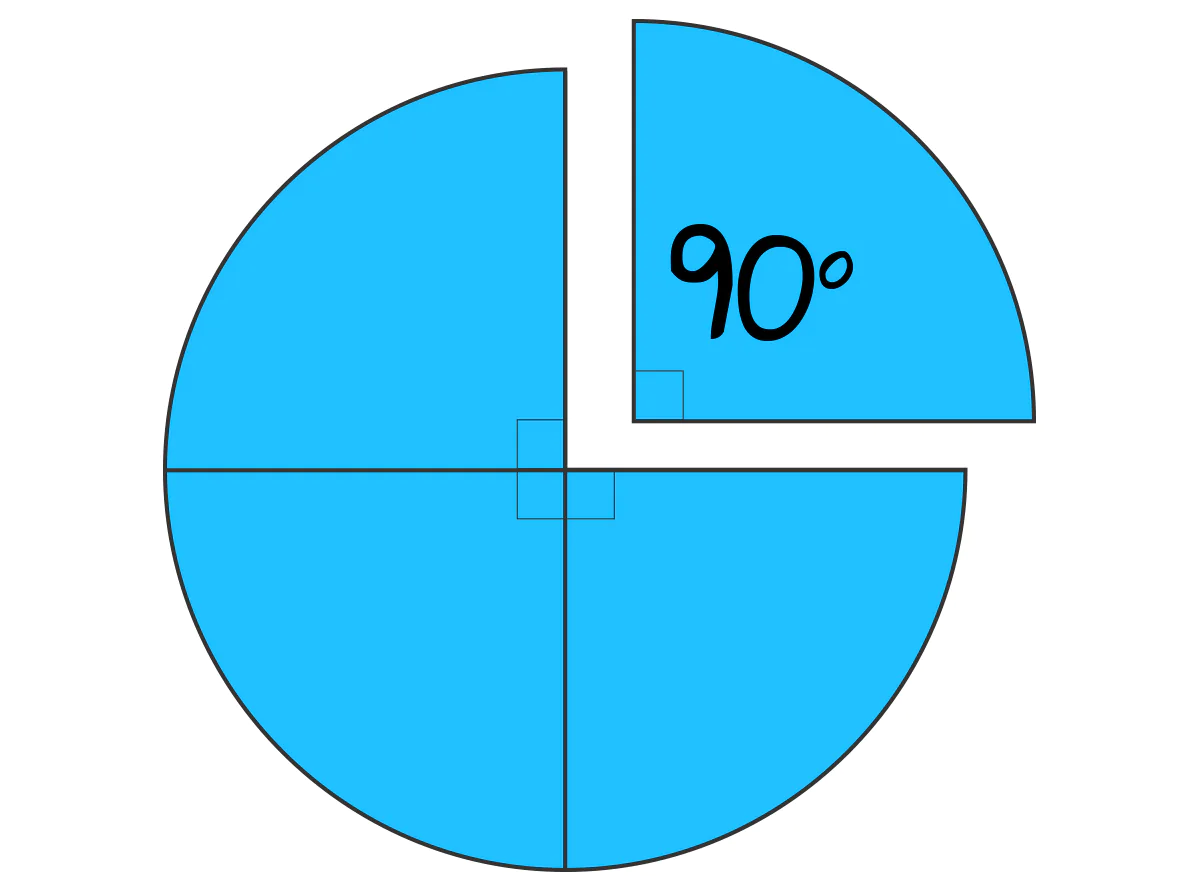
おうぎ形で 中心角が90°ってことは、円の$ \dfrac{1}{4} $です。
だから 半径10mの円の面積を4で割ってます。
高さ5cmの立体があります。底面は中心角が120°、半径6cmのおうぎ形です。この立体の体積を求めよ。

答え & 解説
答え 188.4cm³
6×6×3.14÷3 ×5=188.4
おうぎ形の底面積 × 高さ =188.4
中心角が120°のおうぎ形の面積をださなきゃね
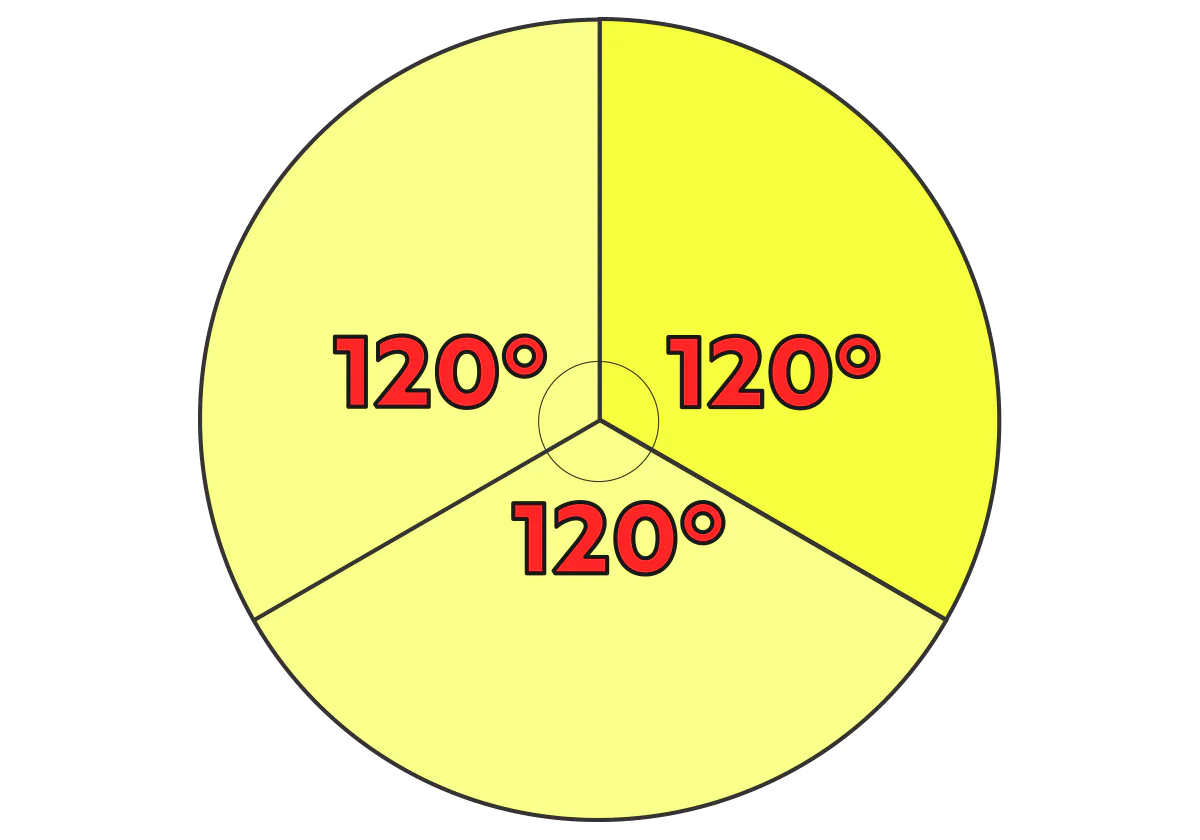
中心角が120°は、円の$ \dfrac{1}{3} $だ。
360÷120=3 だもんね~
だから 半径6cmの円の面積を3で割ってます。
つぎの角柱の体積と!表面積を! 求めてほしいのよ。
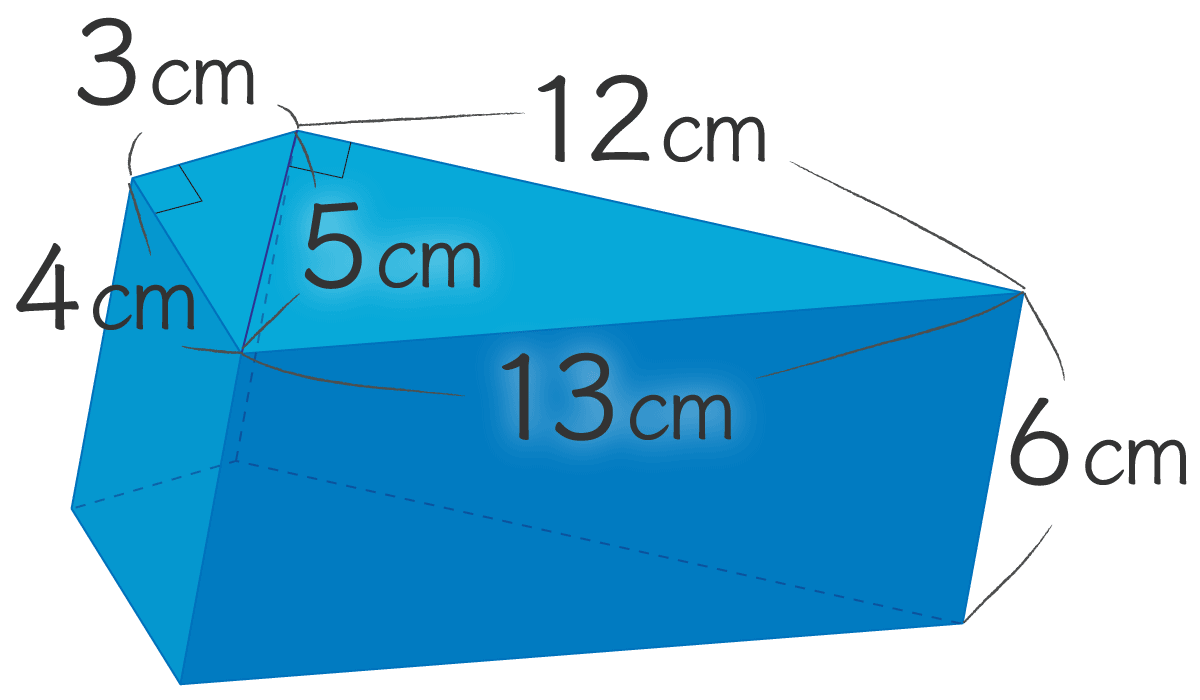
答え & 解説
体積 216cm³
表面積 264cm²
解き方 ~ 体積
底面積 × 高さ = 体積
まずはこの底面積を求めなきゃ始まらない。赤と黒のしましまでおしゃれにした底面を見よ!
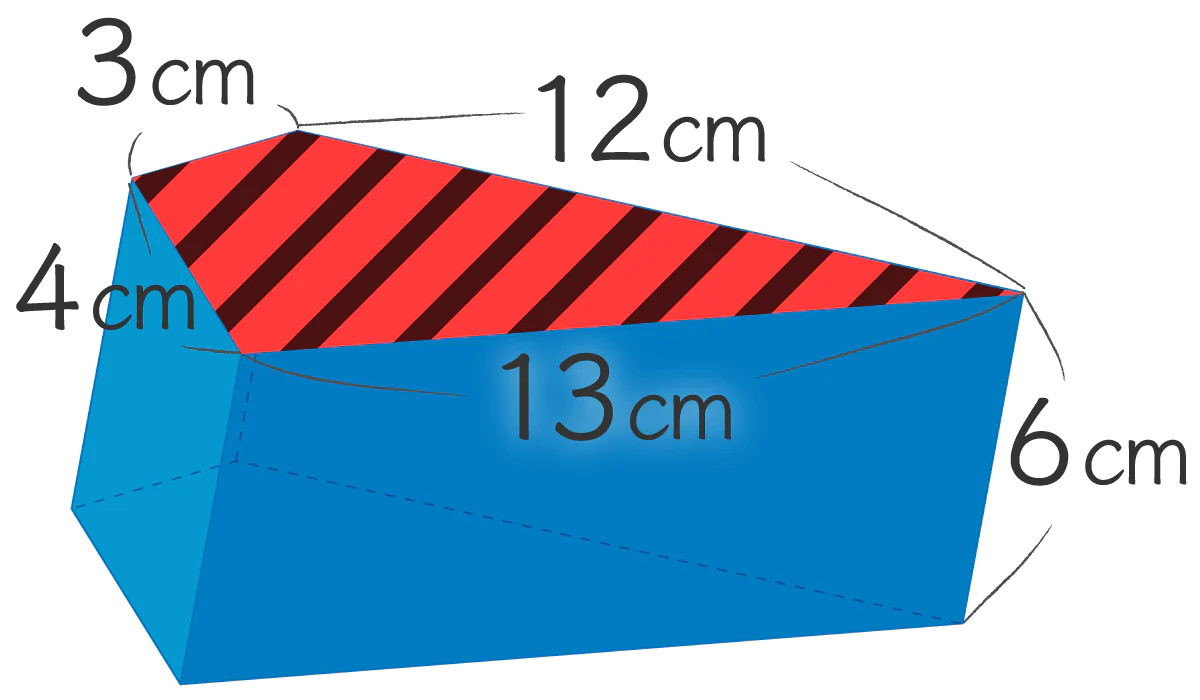
え~、見にくいですね。赤黒で目がチカチカします。
この立体の底面は 2つの直角三角形でできてるから、
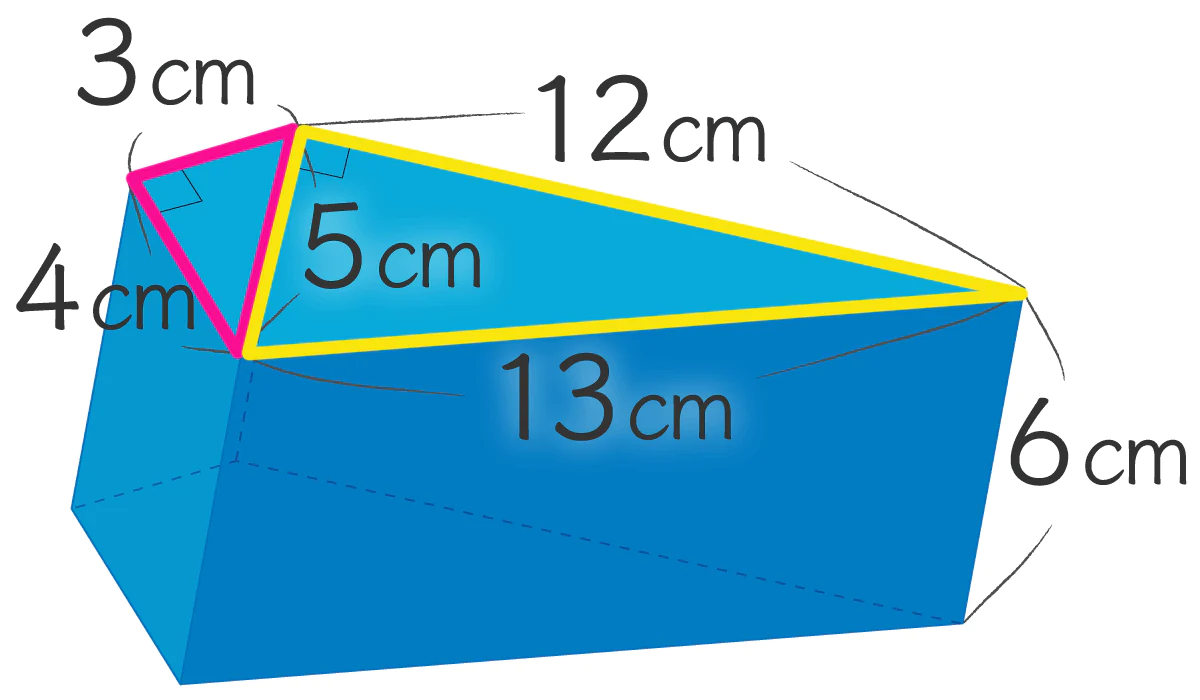
直角三角形の面積を足せば この立体の底面積 ってことで、このように計算してみます↓
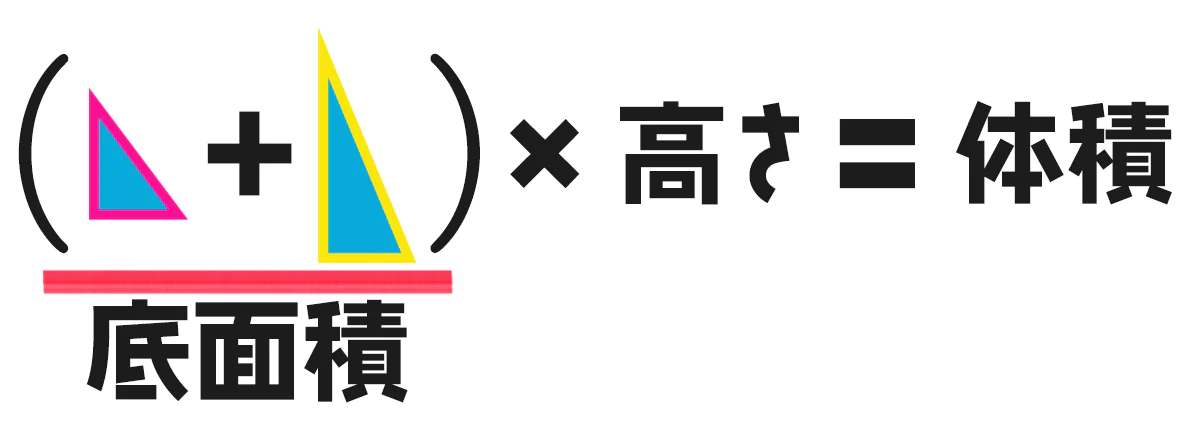
じゃあ、式を立ててみよう!□をうめてね
解き方 ~ 表面積
底面積 × 2 + 側面積 = 表面積
底面積は体積のときに出したから、側面だけ見てみよう! ちょっと色を変えます。
で、側面を開くと、おなじみの長方形ですね~
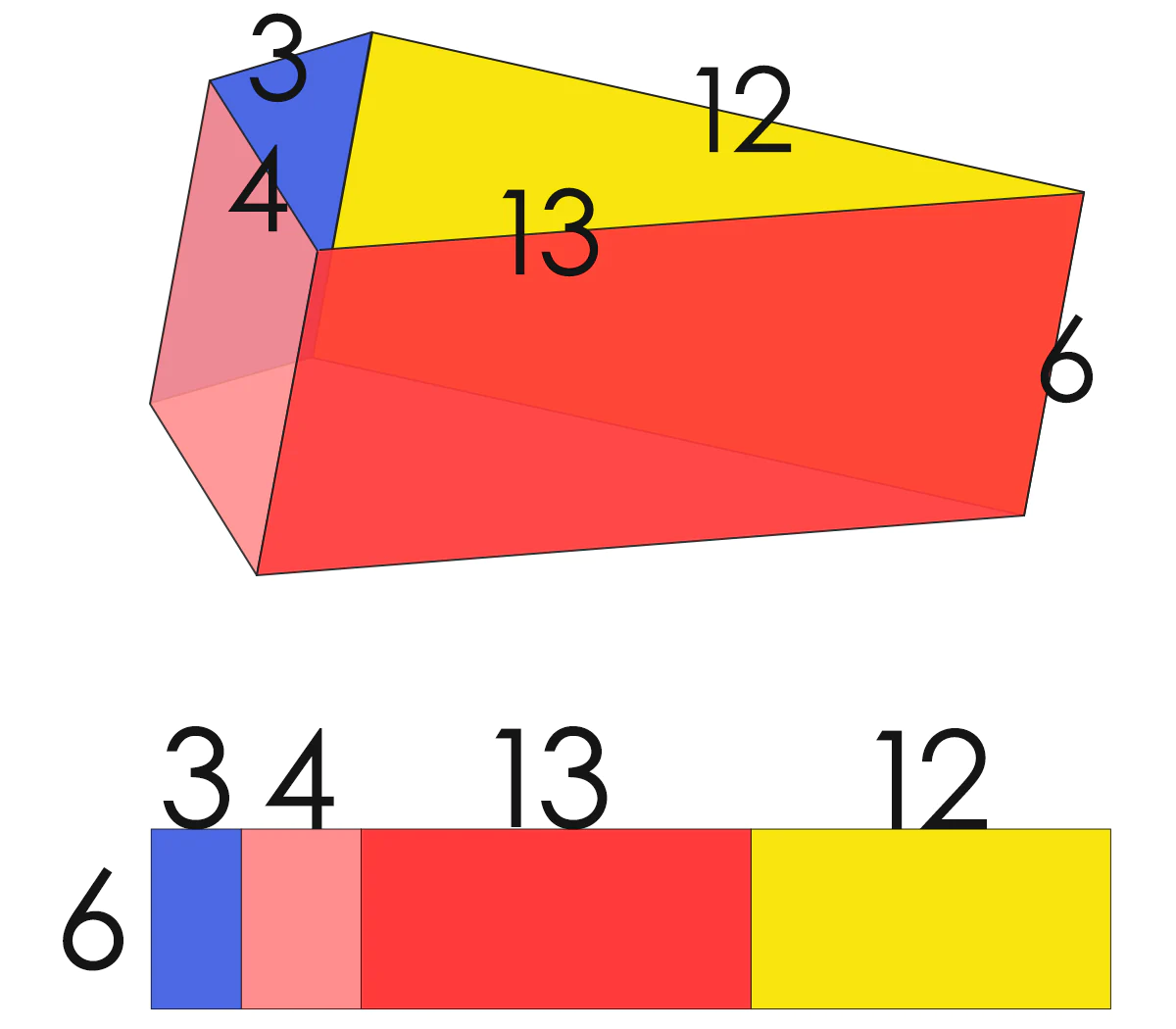
では、
底面積×2 + 側面積 = 表面積 ってことで、こうやって計算してみます↓
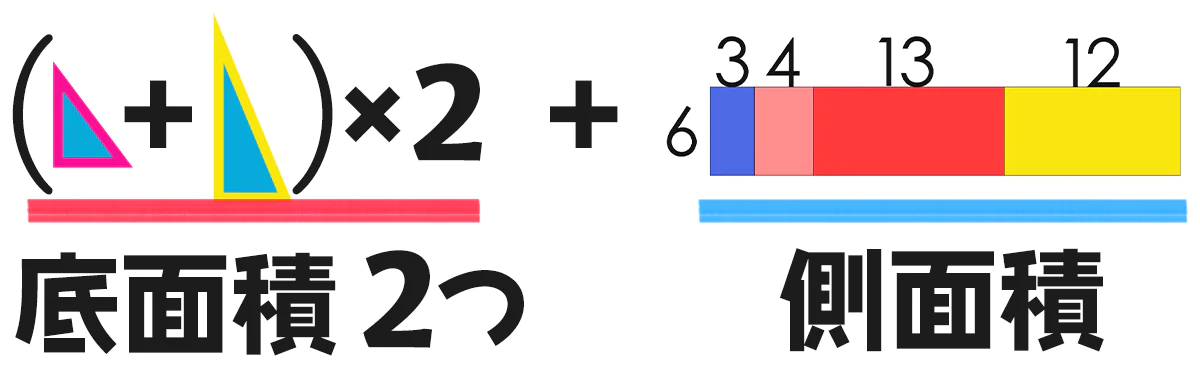
上の通りに式を立ててみよう!□をうめてね。 紙に書いてみるのもおすすめ

\begin{eqnarray} (4 \times 3 \div 2 + 12 \times 5 \div 2) \times 2 + 6 \times (3+4+13+12) &=& \\[0.5em] (6 + 30) \times 2 + 6 \times 32 &=& \\[0.5em] 36 \times 2 + 6 \times 32 &=& \\[0.5em] 72 + 192 &=& 264 \end{eqnarray}
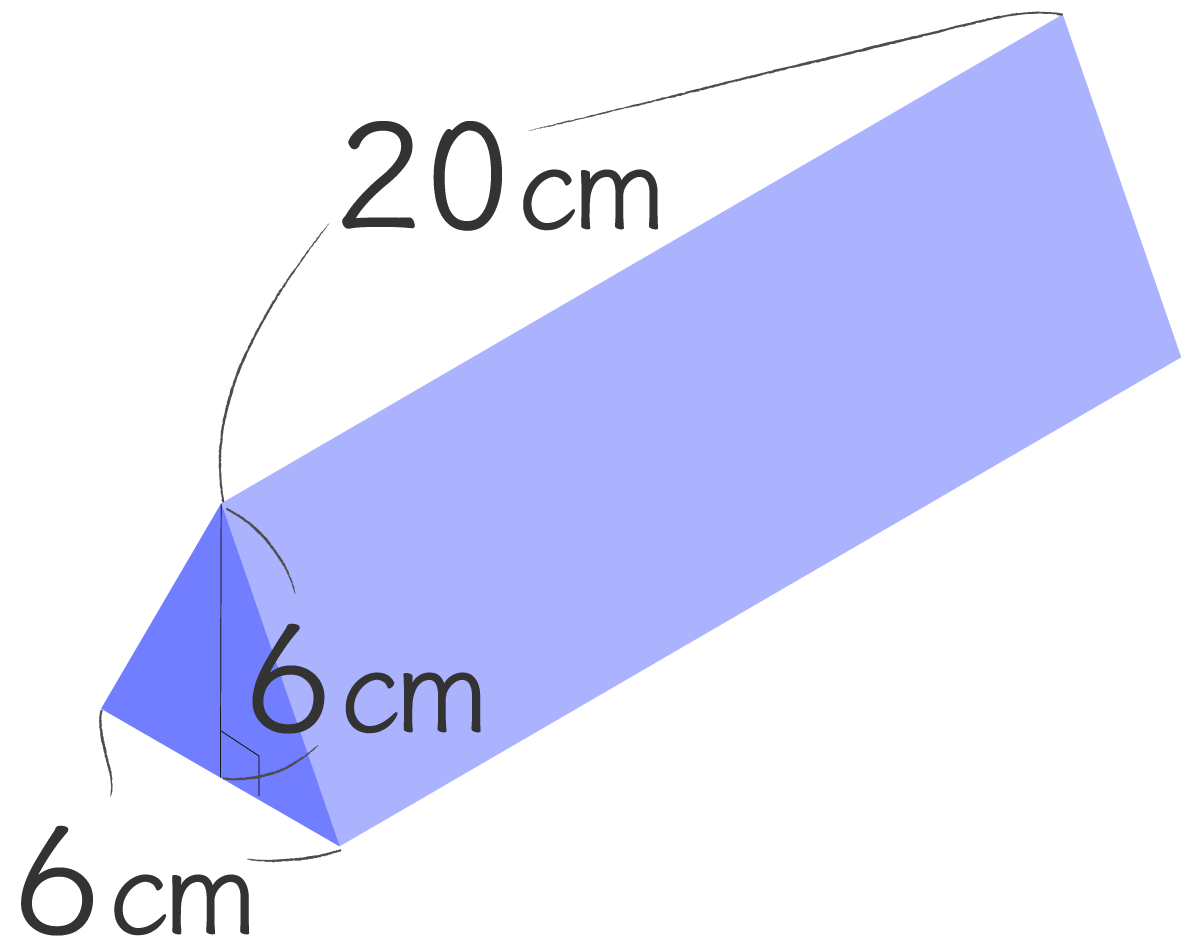
三角柱と直方体を組み合わせた立体の体積を求めよ。
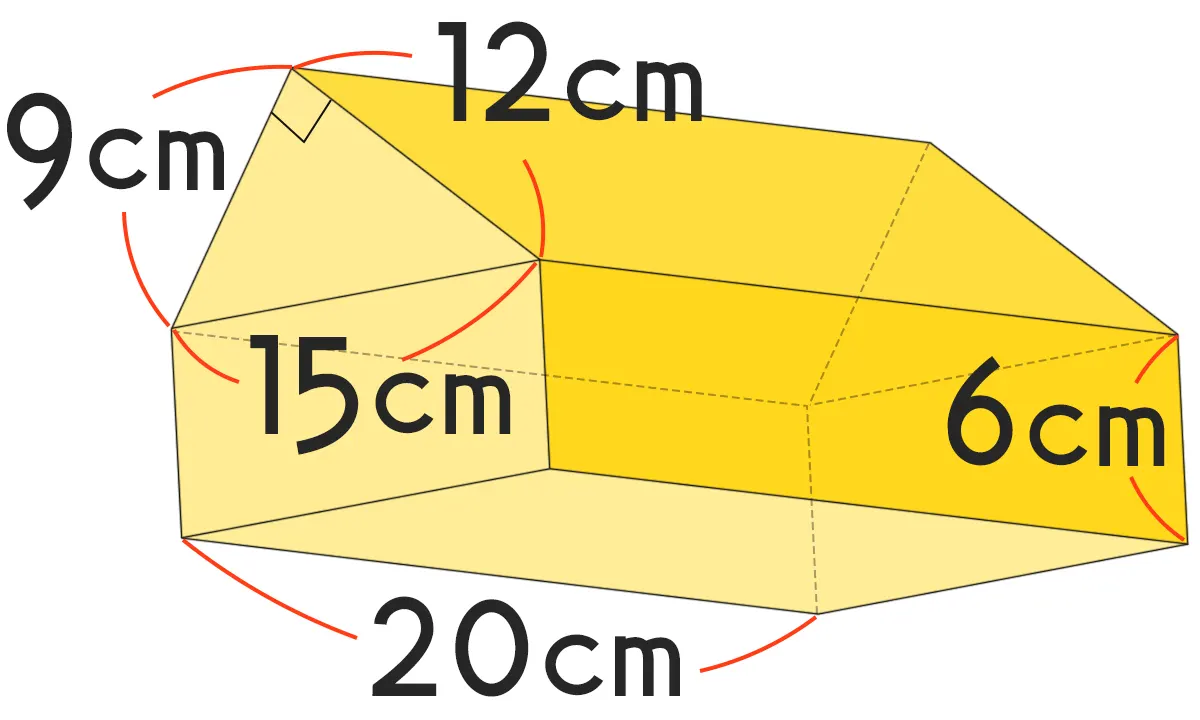
答え & 解説
答え 2880cm³
解き方
三角柱と直方体の体積を足してもいいけど、
「 底面積×高さ」でやってみますね。
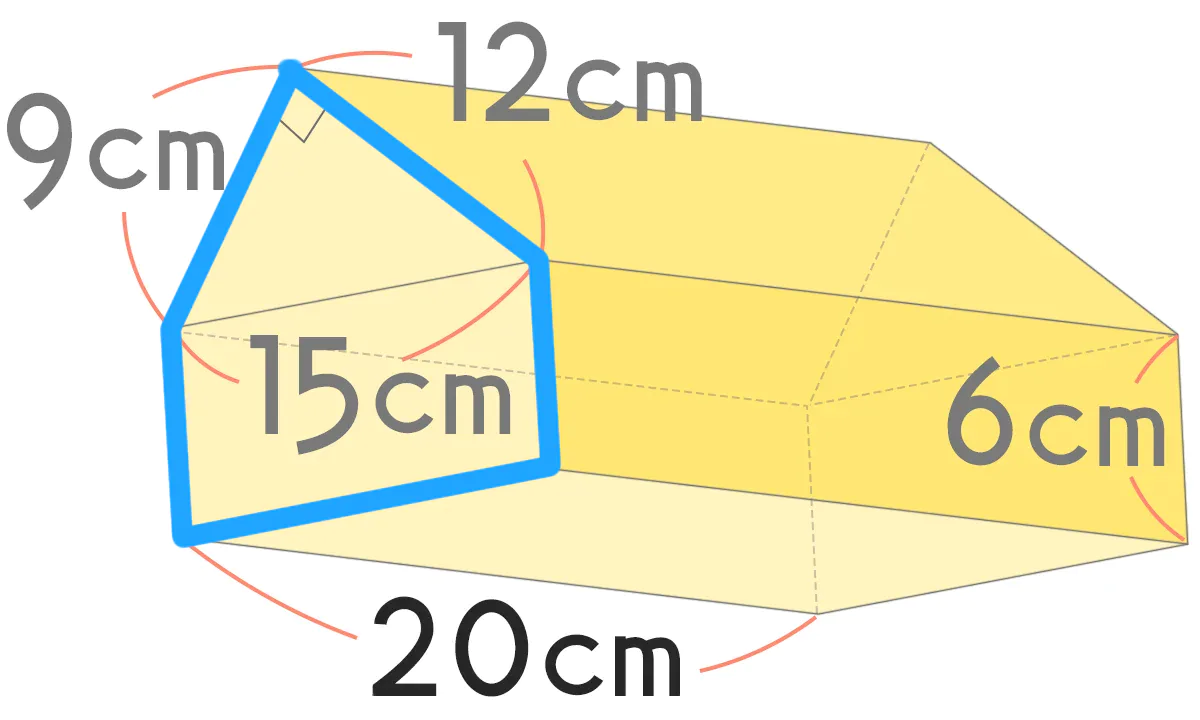
水色で囲った底面積 × 20 です。
底面は、 直角三角形+長方形
\begin{eqnarray} (12 \times 9 \div 2 + 6 \times 15) \times 20 &=& \\[0.5em] (54 + 90) \times 20 &=& \\[0.5em] 144 \times 20 &=& 2880 \end{eqnarray}
直方体から三角柱を切り取った立体があります。この立体の体積は何cm³?
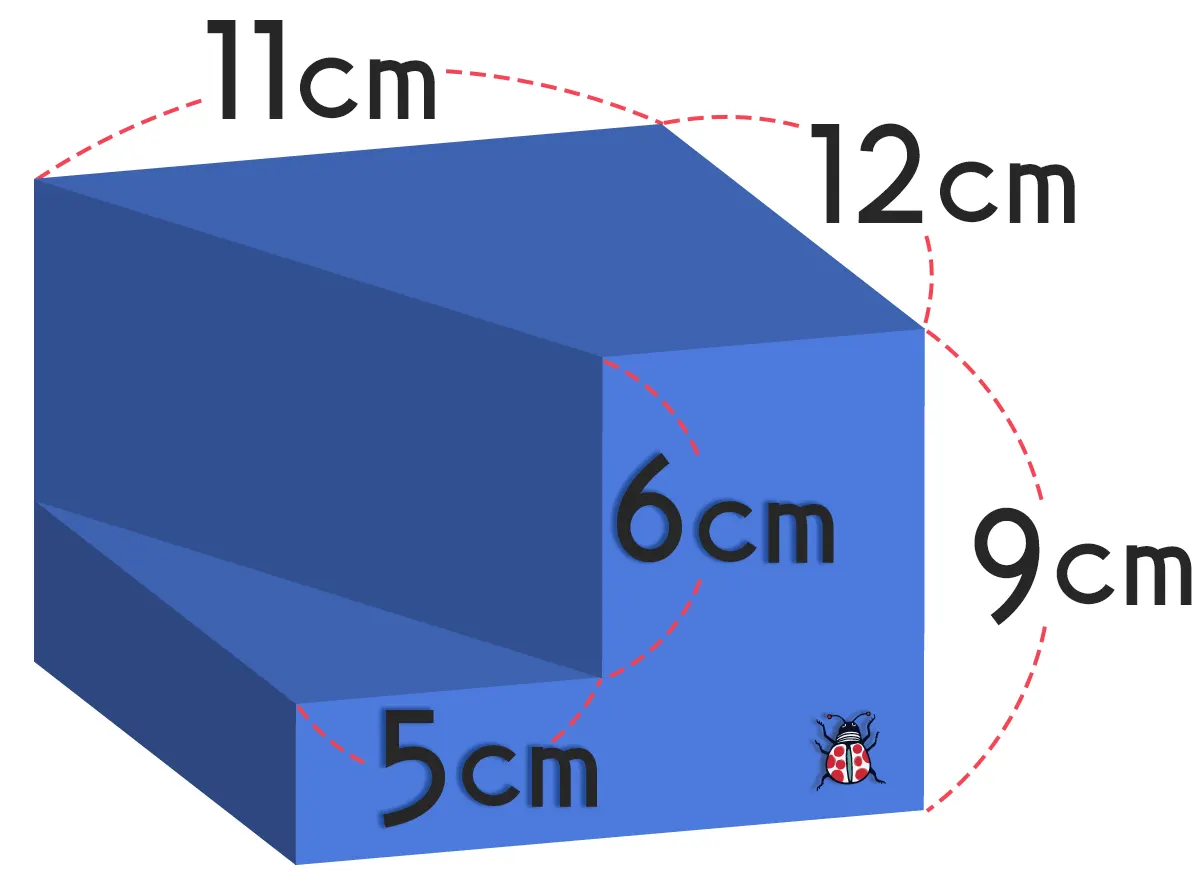
答え & 解説
答え 1008cm³
解き方
直方体から 切り取られた三角柱を引きます。 他のやり方でもOKだよ
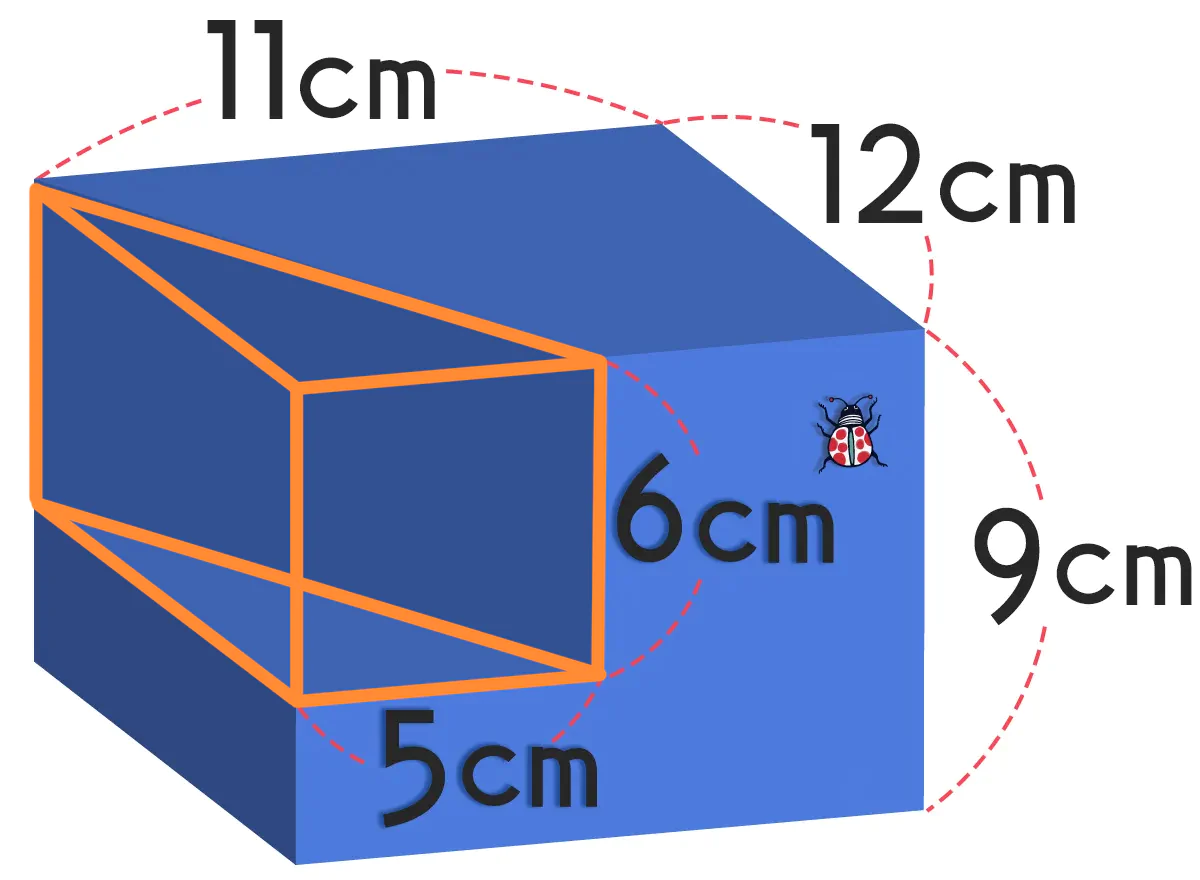
直方体の体積は?
切り取られた三角柱の体積は?
直方体 - 切り取られ三角柱
\begin{eqnarray} 12 \times 11 \times 9 - 5 \times 12 \div 2 \times 6 &=& \\[0.5em] 1188 - 180 &=& 1008 \end{eqnarray}
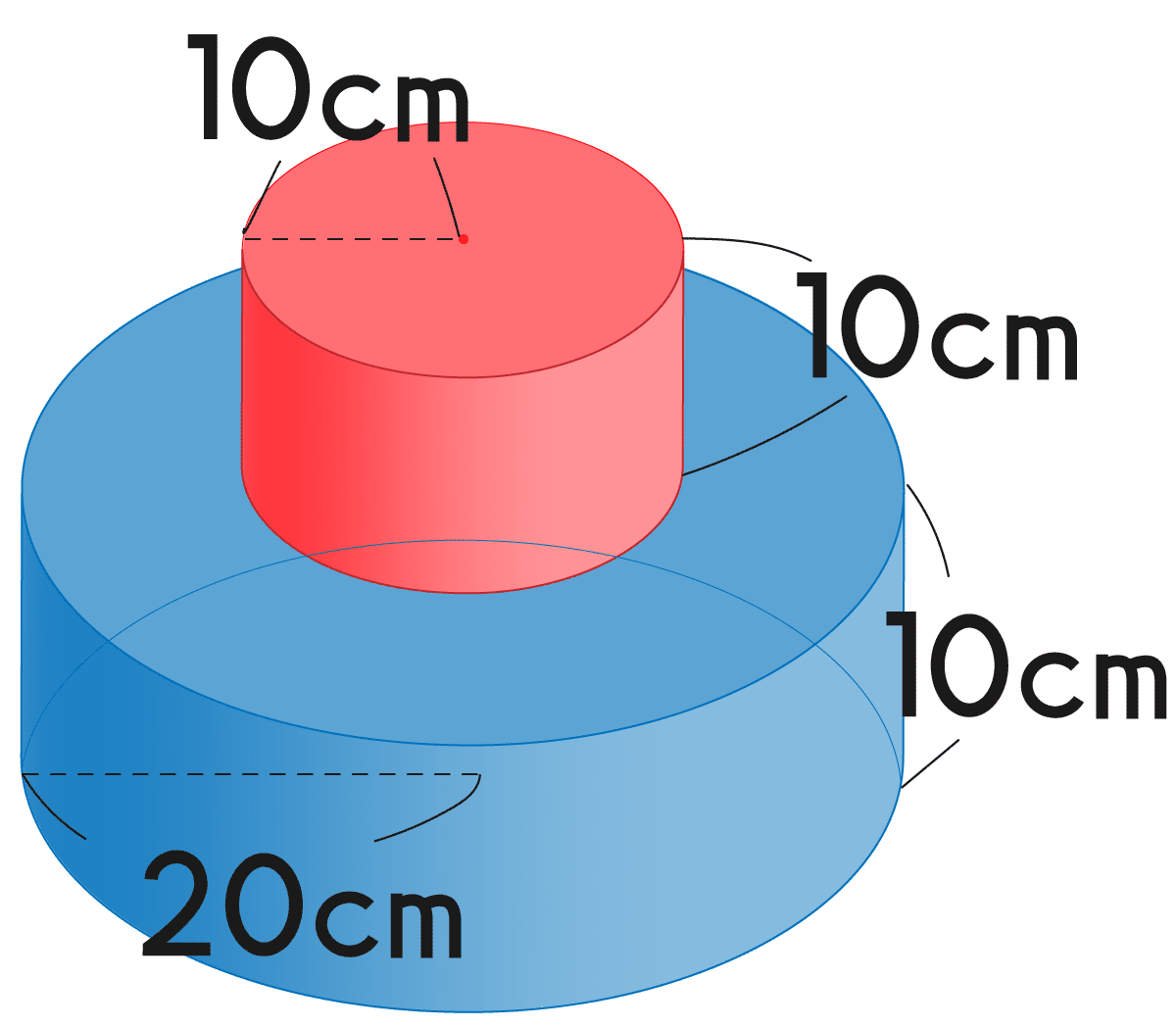
円柱の上に円柱をのせた立体があります。この立体の体積と表面積を求めましょう。
答え & 解説
体積 15700cm³
表面積 4396cm²
解き方 ~ 体積
赤い円柱の体積 + 青い円柱の体積 = でやってみよう。
\begin{eqnarray} 10 \times 10 \times 3.14 \times 10 + 20 \times 20 \times 3.14 \times 10 &=& \\[0.5em] 3140 + 12560 &=& 15700 \end{eqnarray}
解き方 ~ 表面積
どこを計算していけば良いか ”はっきり” させて、落ち着いて解いていくのだ・・・
まずは、どこを計算するか はっきりさせる。
- 底面(上)
- 底面(下)
- 赤の側面
- 青の側面
表面はこれで全部!
ややこしそうなのは 底面(上)
青と赤が重なってなんだかむずかしそう・・
しかーーし! この立体を真上から見ると、
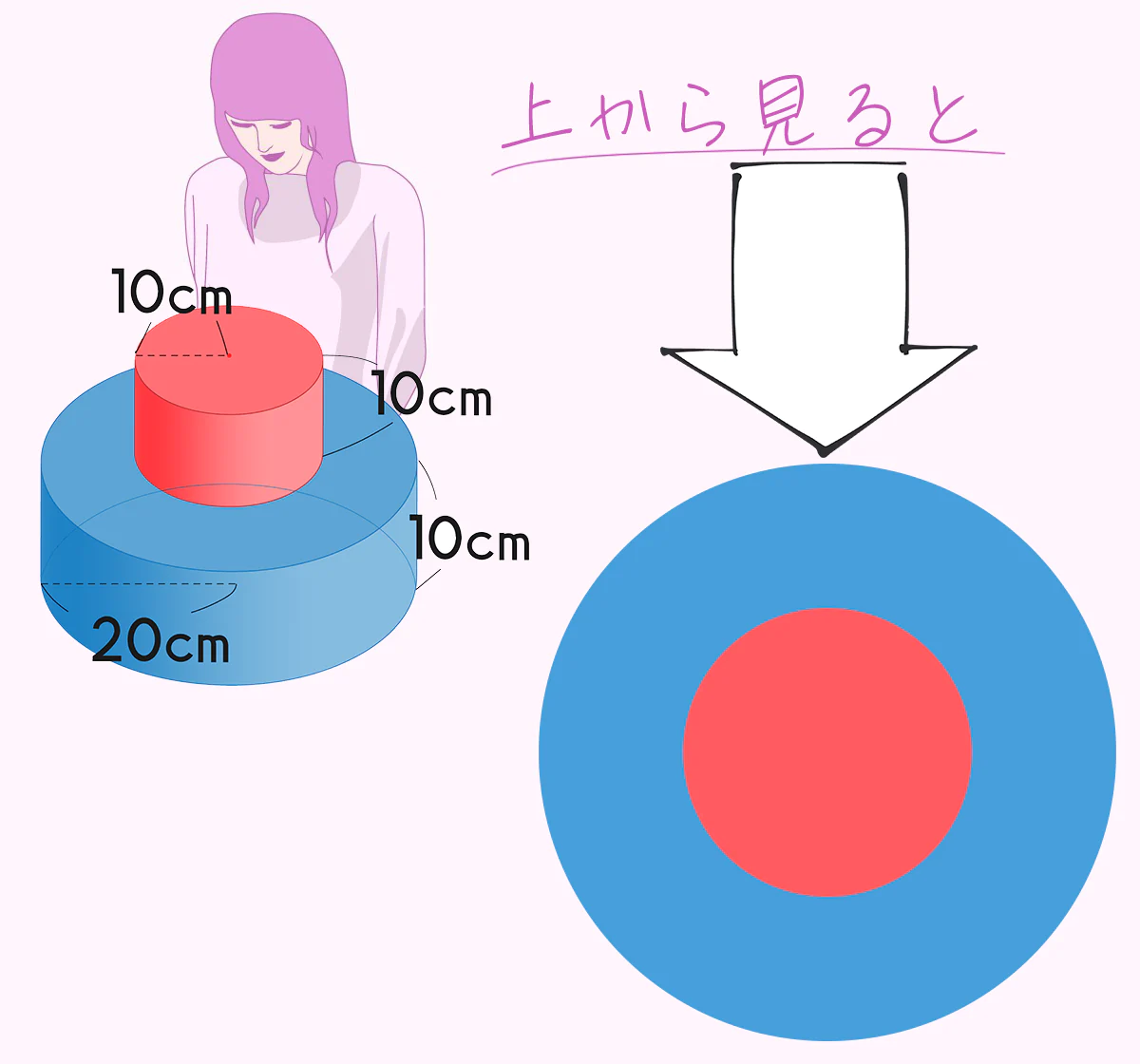
赤と青が重なってるだけで、面積は青の円柱の底面と同じ!
底面2つ+赤の側面+青の側面=
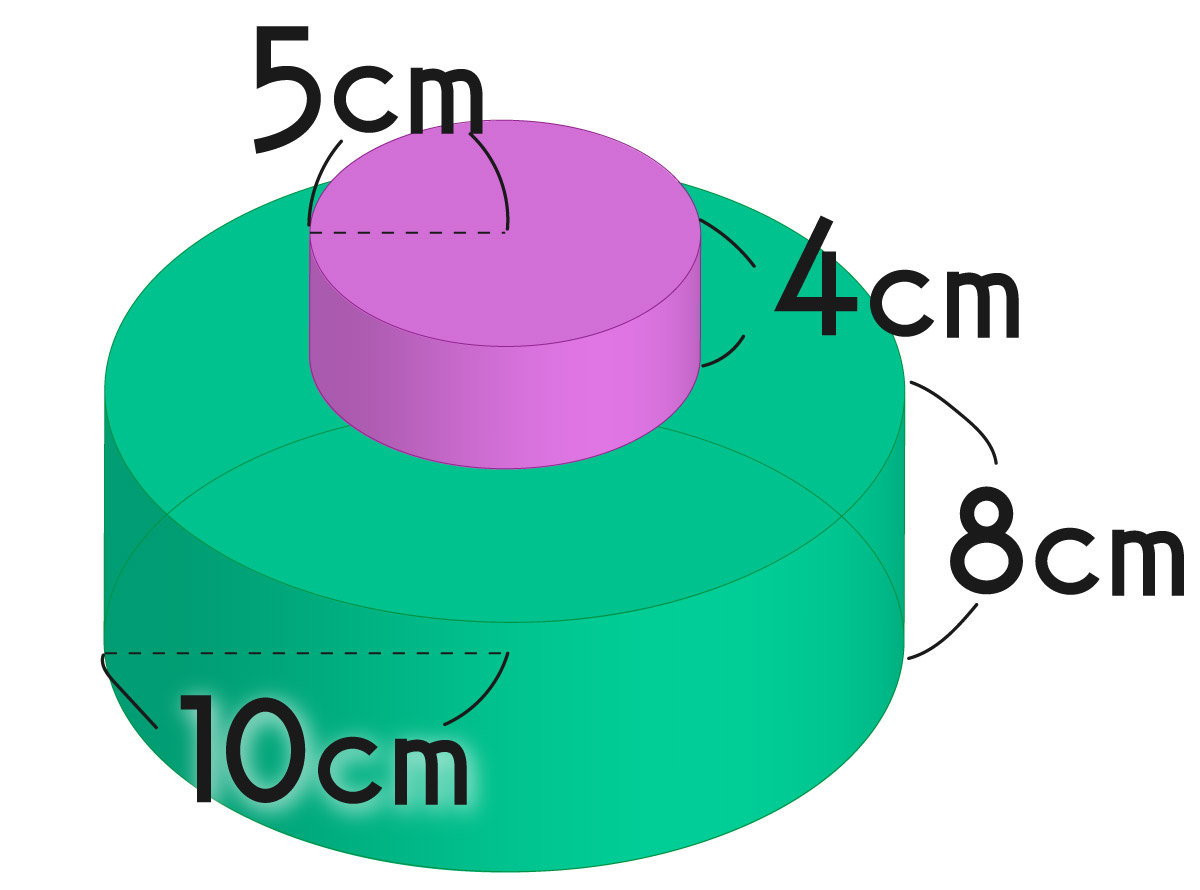
円柱の上に円柱をのせた立体があります。この立体の体積と表面積を求めましょう。
答え & 解説
体積 2826cm³
5×5×3.14×4 + 10×10×3.14×8 = 2826
表面積 1256cm²
10×10×3.14×2 + 4×5×2×3.14 + 8×10×2×3.14=1256
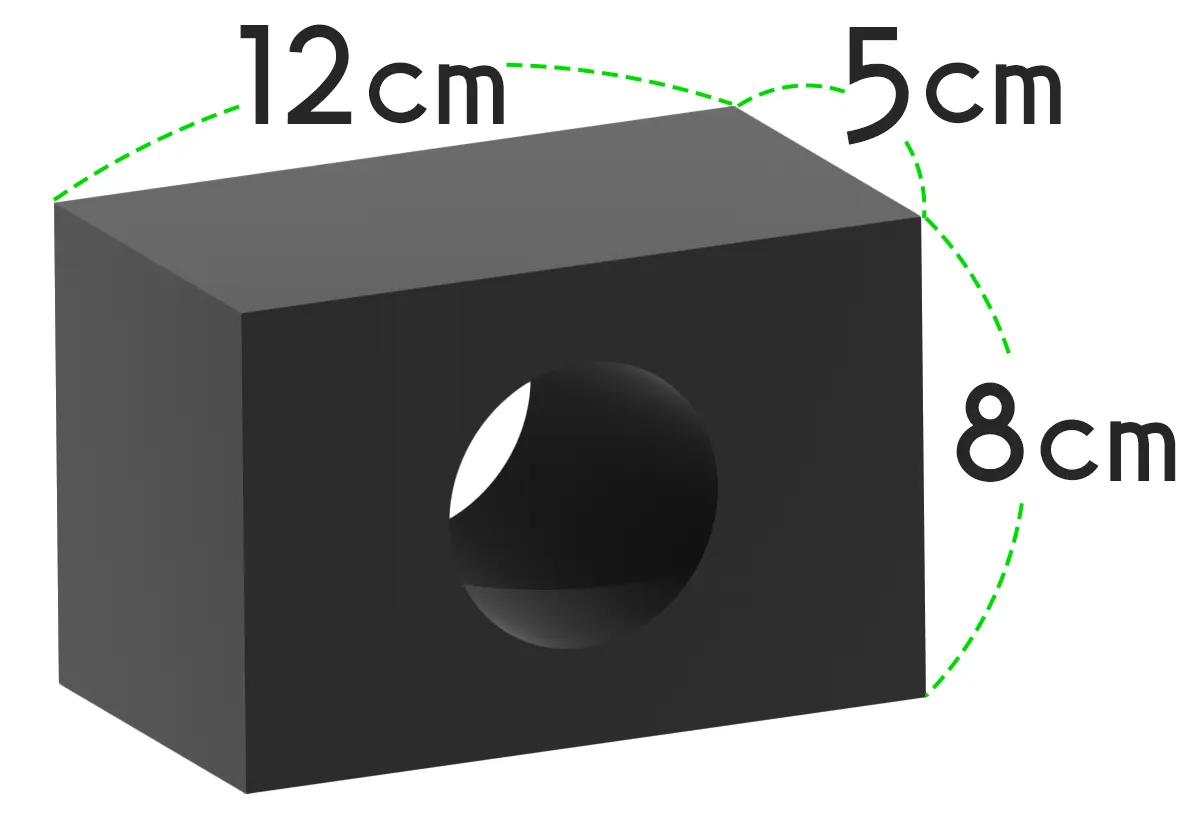
直方体から円柱をくり抜いた立体の体積は? くり抜いた円柱の底面は直径6cmです。
答え & 解説
答え 338.7cm³
直方体の体積 - 円柱の体積 =
これで答えを出した人が多いと思います! なので、
「 底面積×高さ 」 こっちでやってみます。
しましまのとこが底面。
底面積は?
底面積×高さ=体積
式を1行でやってみると
\begin{eqnarray} (12 \times 8 - 3 \times 3 \times 3.14) \times 5 &=& \\[0.5em] (96 - 28.26) \times 5 &=& \\[0.5em] 67.74 \times 5 &=& 338.7 \end{eqnarray}
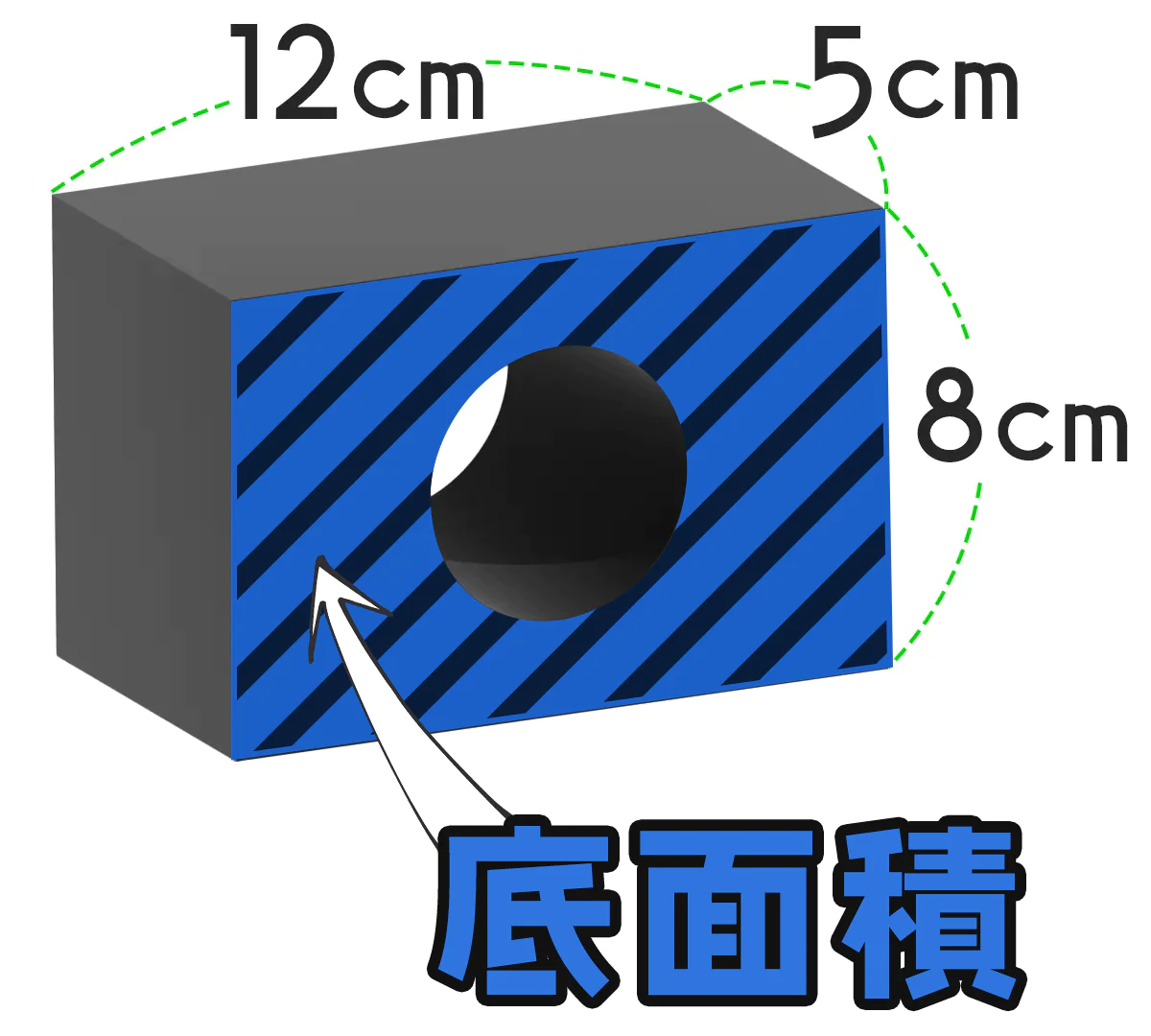
円柱から四角柱をくり抜いた立体の体積と表面積を求めよ。円柱の底面は半径5cm、高さは20cmです。くり抜いた四角柱の底面は1辺3cmの正方形、高さは円柱と同じです。

答え & 解説
体積 1390cm³
表面積 1007cm²
解き方 ~ 体積
「 底面積×高さ 」 これで体積を求めてみる。

円から正方形を引いたのが底面積~
底面積は?
底面積×高さ=体積
式を1行でやってみると
\begin{eqnarray} (5 \times 5 \times 3.14 - 3 \times 3) \times 20 &=& \\[0.5em] (78.5 - 9) \times 20 &=& \\[0.5em] 69.5 \times 20 &=& 1390 \end{eqnarray}
解き方 ~ 表面積
この立体の表面積はこんな感じ
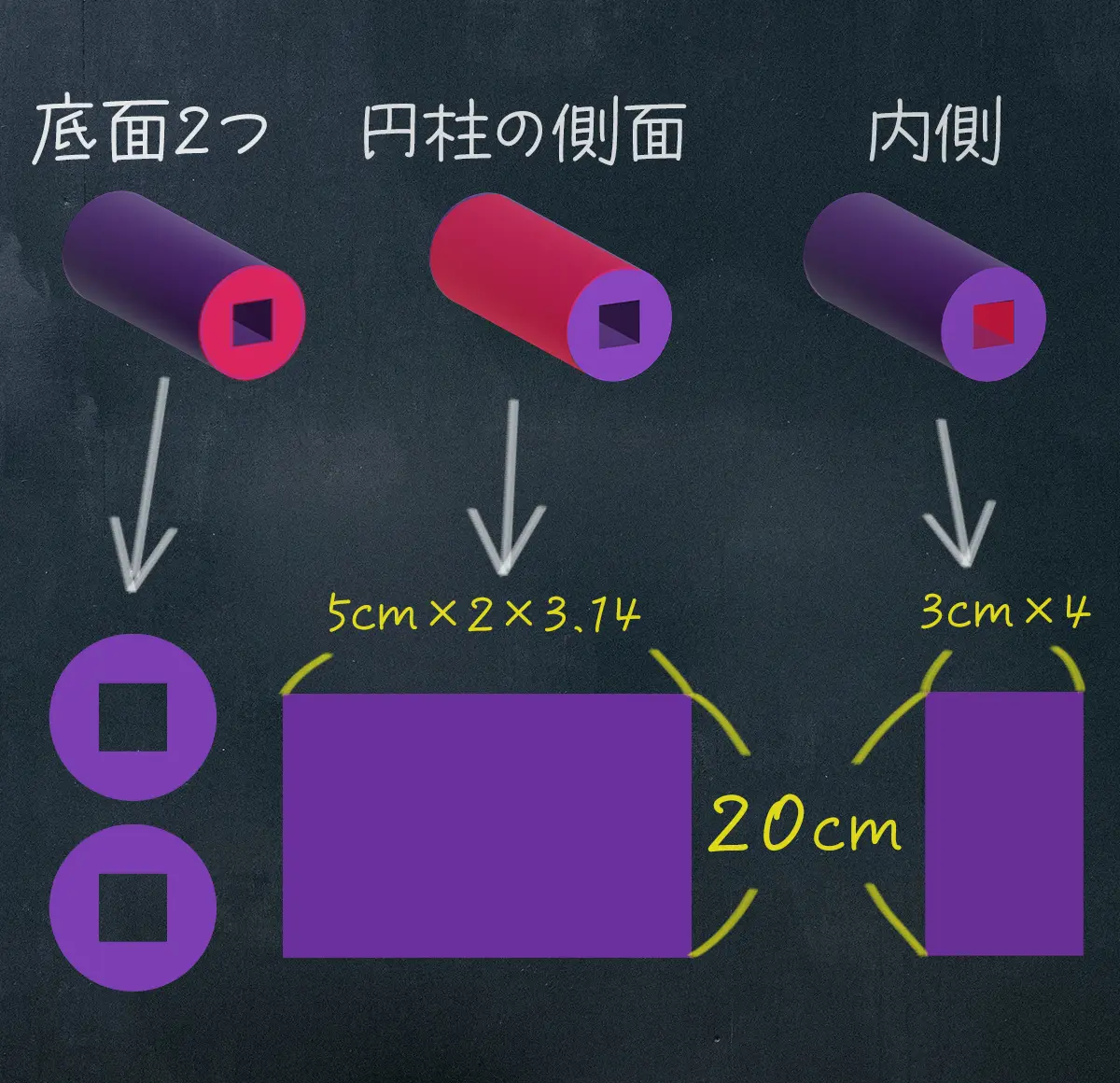
底面積は?
円柱の側面積は?
内側の面積は?
全部足せば表面積
式を1行でやってみる
( 底面 )×2 + 円柱側面 + 内側
\begin{eqnarray} (5 \times 5 \times 3.14 - 3 \times 3) \times 2 + 20 \times 5 \times 2 \times 3.14 + 20 \times 3 \times 4 &=& \\[0.5em] 69.5 \times 2 + 20 \times 5 \times 2 \times 3.14 + 20 \times 3 \times 4 &=& \\[0.5em] 139 + 628 + 240 &=& 1007 \end{eqnarray}
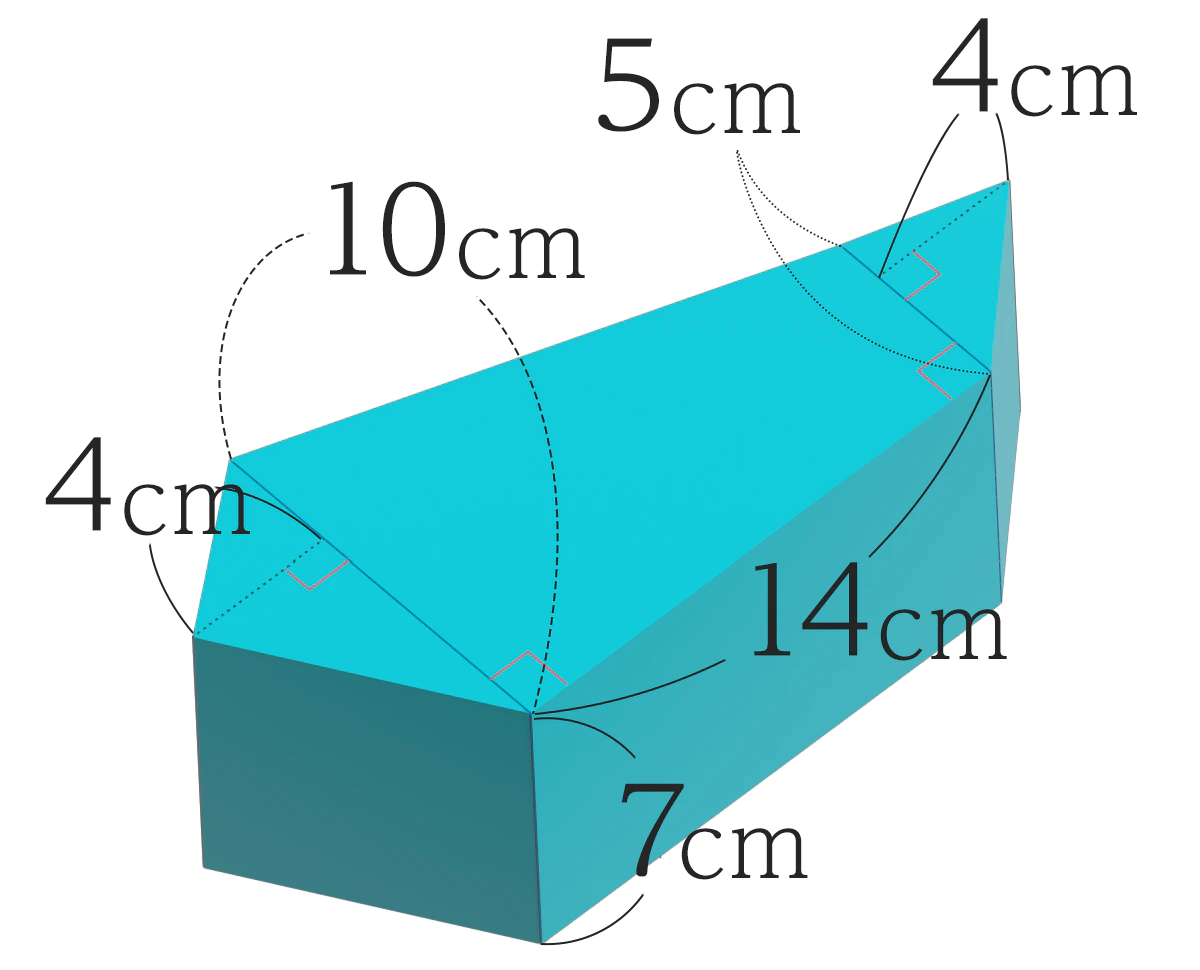
下の立体の体積を求めましょう。
答え & 解説
答え 945cm³

底面積×高さ=体積
底面は、三角形2つと台形を組み合わせた形 ですよね
じゃあ、底面積だしましょう。

奥の三角形 + 手前の三角形 + 台形
底面積×高さ=体積
この立体の体積を求めてください。お願いします!
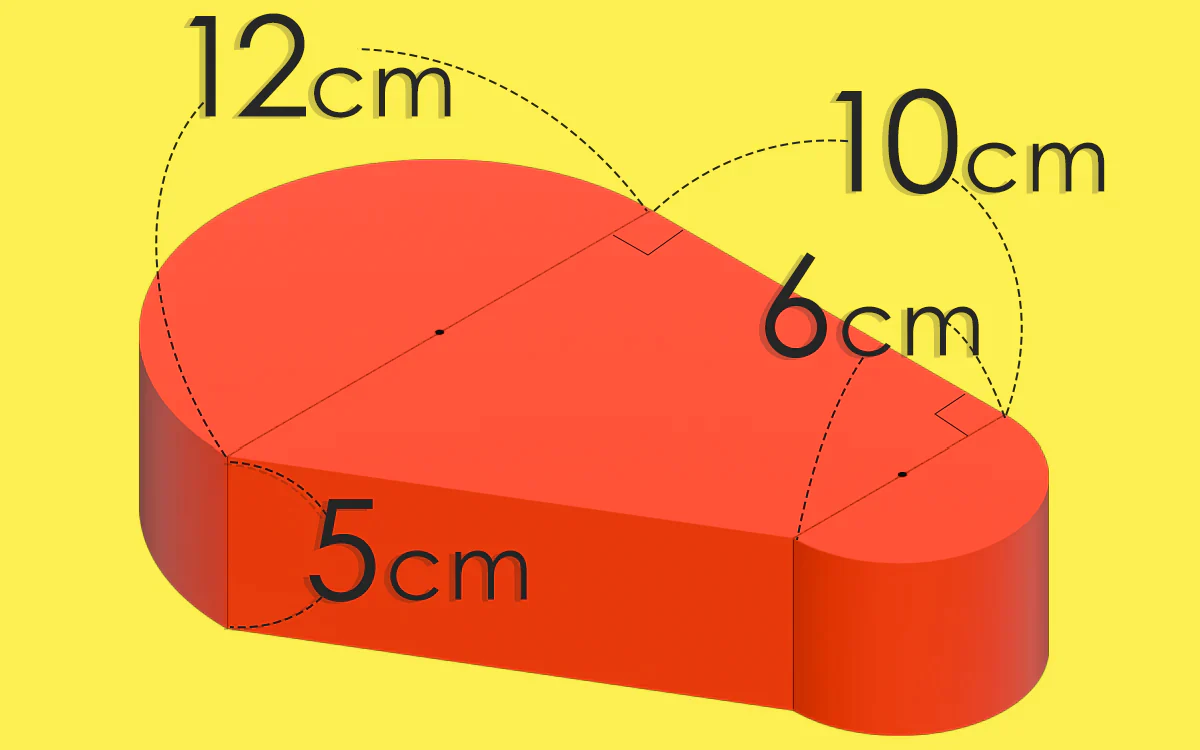
答え & 解説
答え 803.25cm³
「底面積×高さ=体積」でやってみよう。まずは底面積~
小さい半円 + 大きい半円 + 台形
底面積×高さ=体積
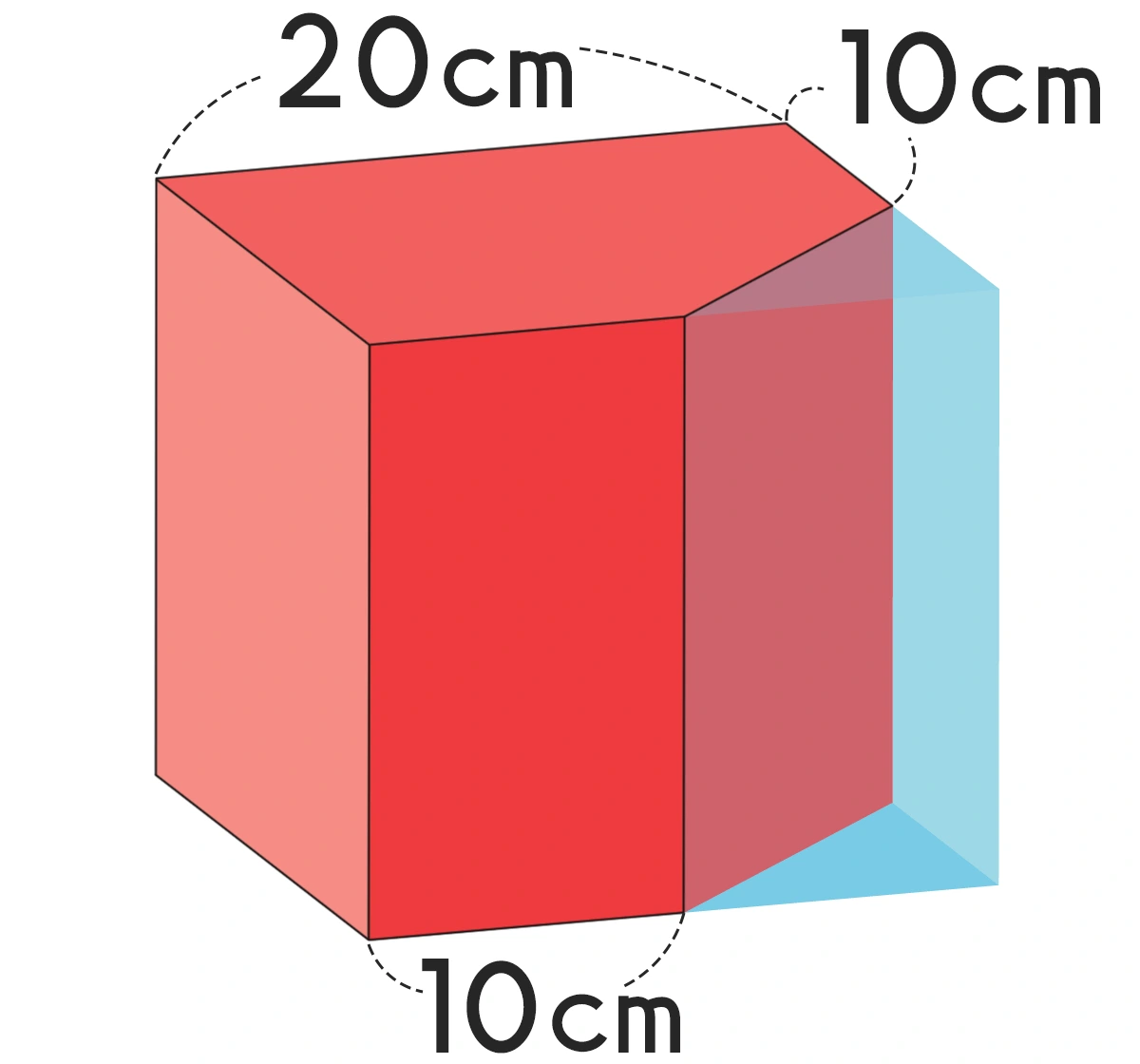
1辺20cmの立方体から三角柱を切り取りました。この立体の体積は何cm³ですか。
答え & 解説
答え 7000cm³
立方体の体積から 三角柱の体積を引いてもいいけど、底面積×高さ=体積 でやってみる。

底面は 『正方形-三角形』
直方体の容器にねんどで作った円柱を入れた。容器の内のりは1辺20cmの正方形で、深さは40cmだ。次の問題に答えよ。

- 円柱の体積は何cm³ですか。円柱は容器にピッタリ入っている。
- この容器の隙間に水をいっぱいになるまで入れ、そーっと円柱を取り出す。水面の高さは容器の底から何cmでしょう。
- その水を捨てさっきのねんどをもどします。 ねんどの形を容器に沿って四角柱にしました。この時ねんどの高さは何cmでしょう。

答え & 解説
- 12560cm³10×10×3.14×40=12560
- 8.6cm
- 31.4cm
2問目の解説:水の高さ
すきまに水を入れましょ。
ねんどが溶けたり浮いたりしそう? たしかに・・・でも今回は溶けないし浮かない!っつーことでお願いします。

水の容積は何cm³か。
容積っていうのは【容器に入っている量】のことね。

容器の容積から 円柱の体積を引けば 水の容積よね。
じゃあ さっそく水の容積をだしましょ~。円柱の体積は12560cm³ って1問目で出したから、
20×20×40 - 12560 =3440
水の容積は 3440cm³
円柱を取り出すとこんな感じですかね
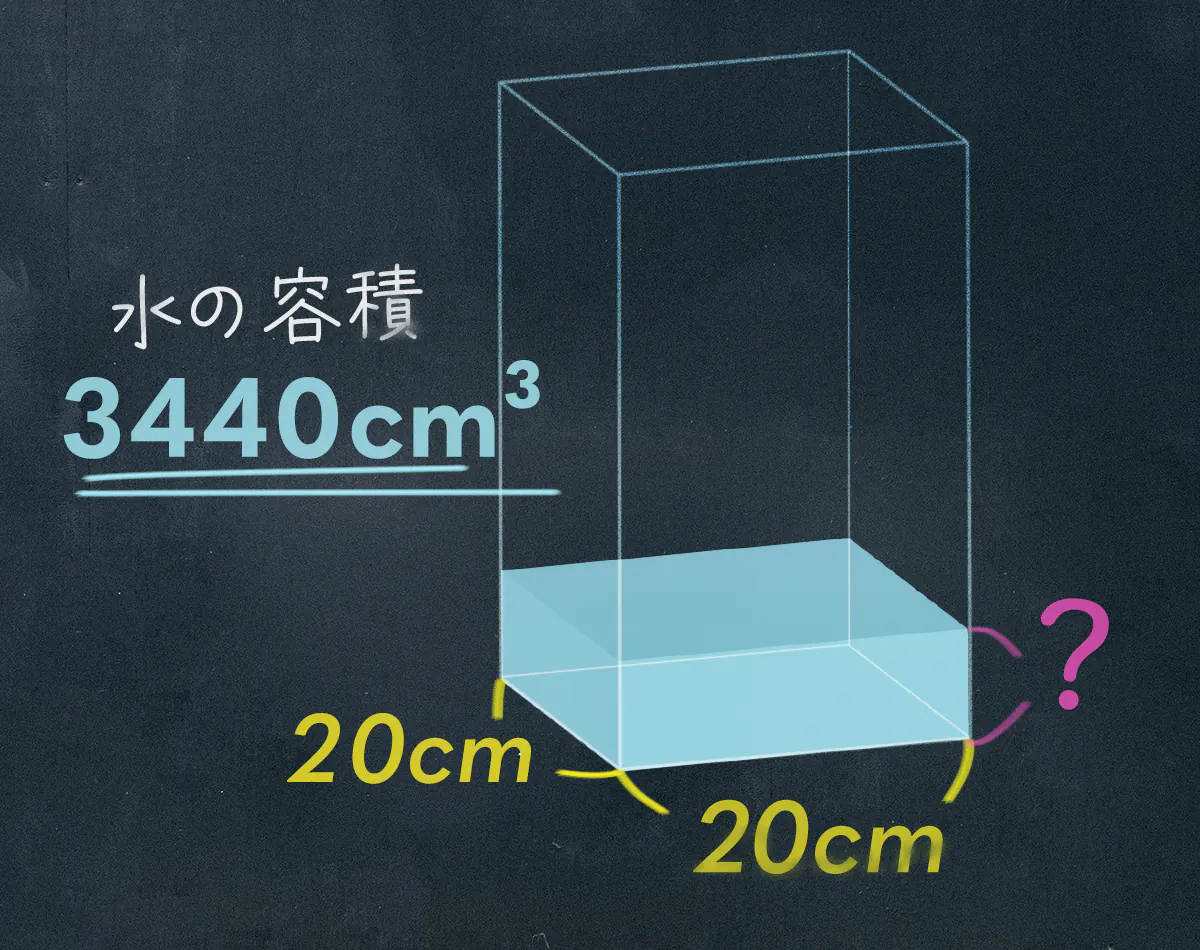
水の高さを□にすると、
計算やってみる
\begin{eqnarray} 20 \times 20 \times \Box &=& 3440 \\[0.5em] 400\times \Box &=& 3440 \\[0.5em] \Box &=& 3440 \div 400 \\[0.5em] \Box &=& 8.6 \end{eqnarray}

2問目の答えは8.6cm
3問目:形が変わったねんどの高さ
容器に入れたねんどはこんな感じよね
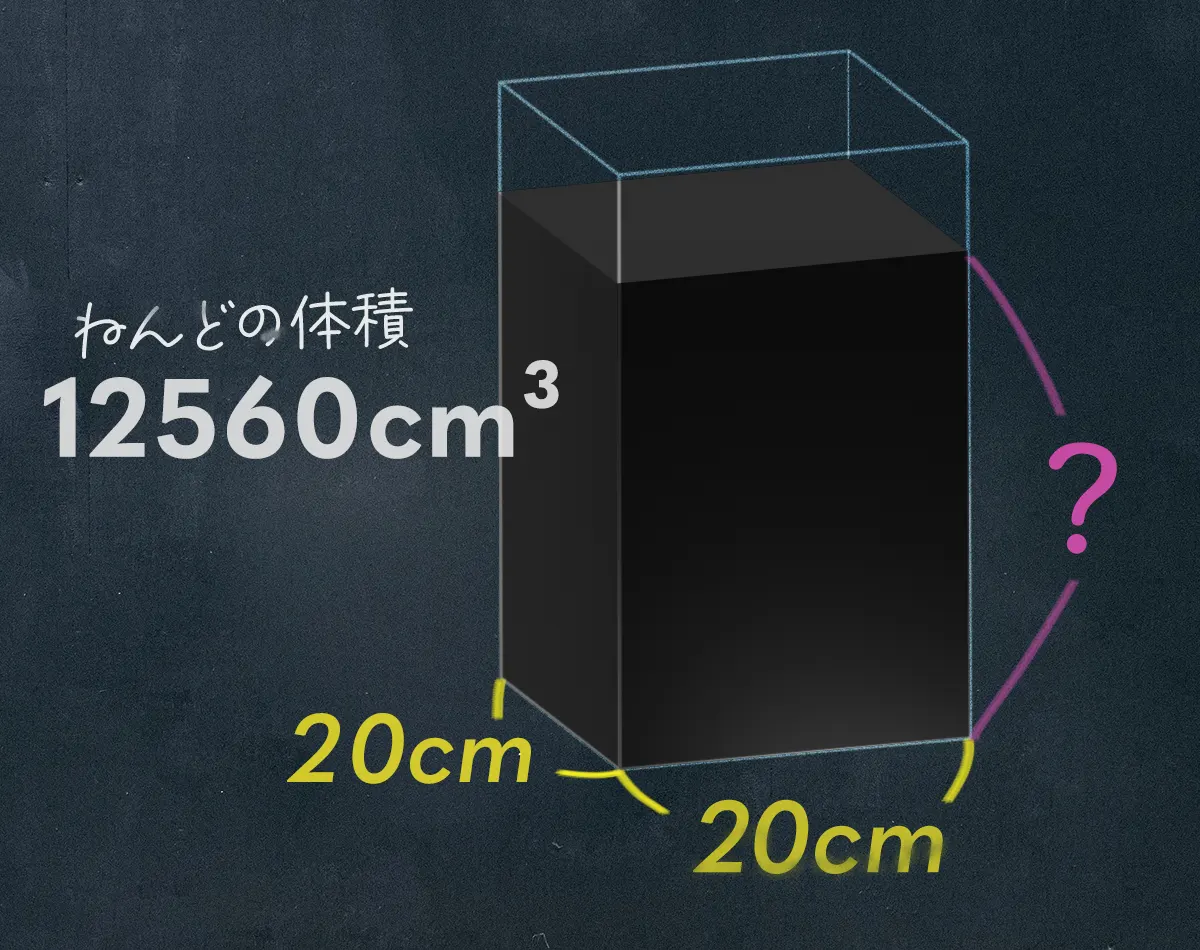
底面積と体積が分かってるから 高さが出せちゃう! さっきの水の高さと同じだね。
というわけで答えは31.4cm³

ちょっとまった。こんなのもあるよ。
水とねんどで容器ピッタリなんだよね。こんなふうに
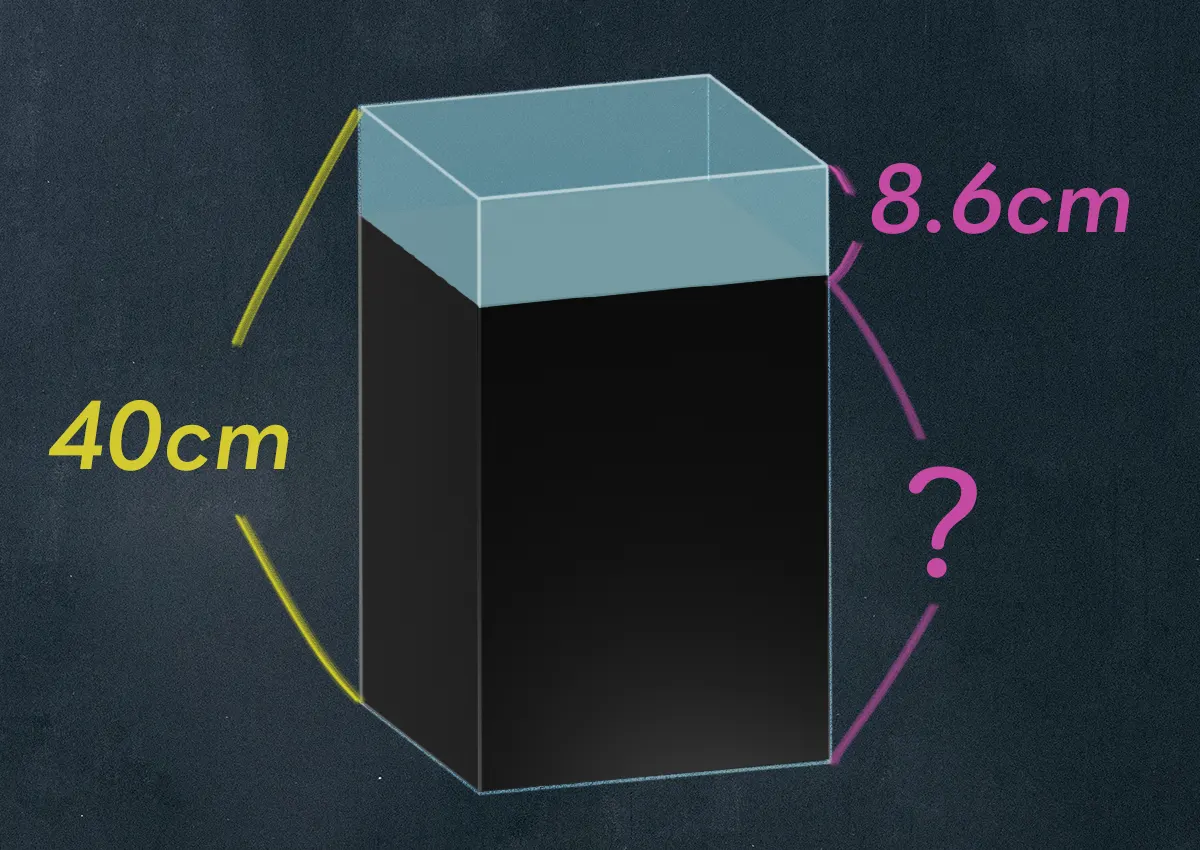

水の高さは8.6cmだった。
容器の深さは40cmだから
40-8.6=31.4
なるほどっす!
円柱から円柱をくり抜いた立体があります。この立体の体積は?
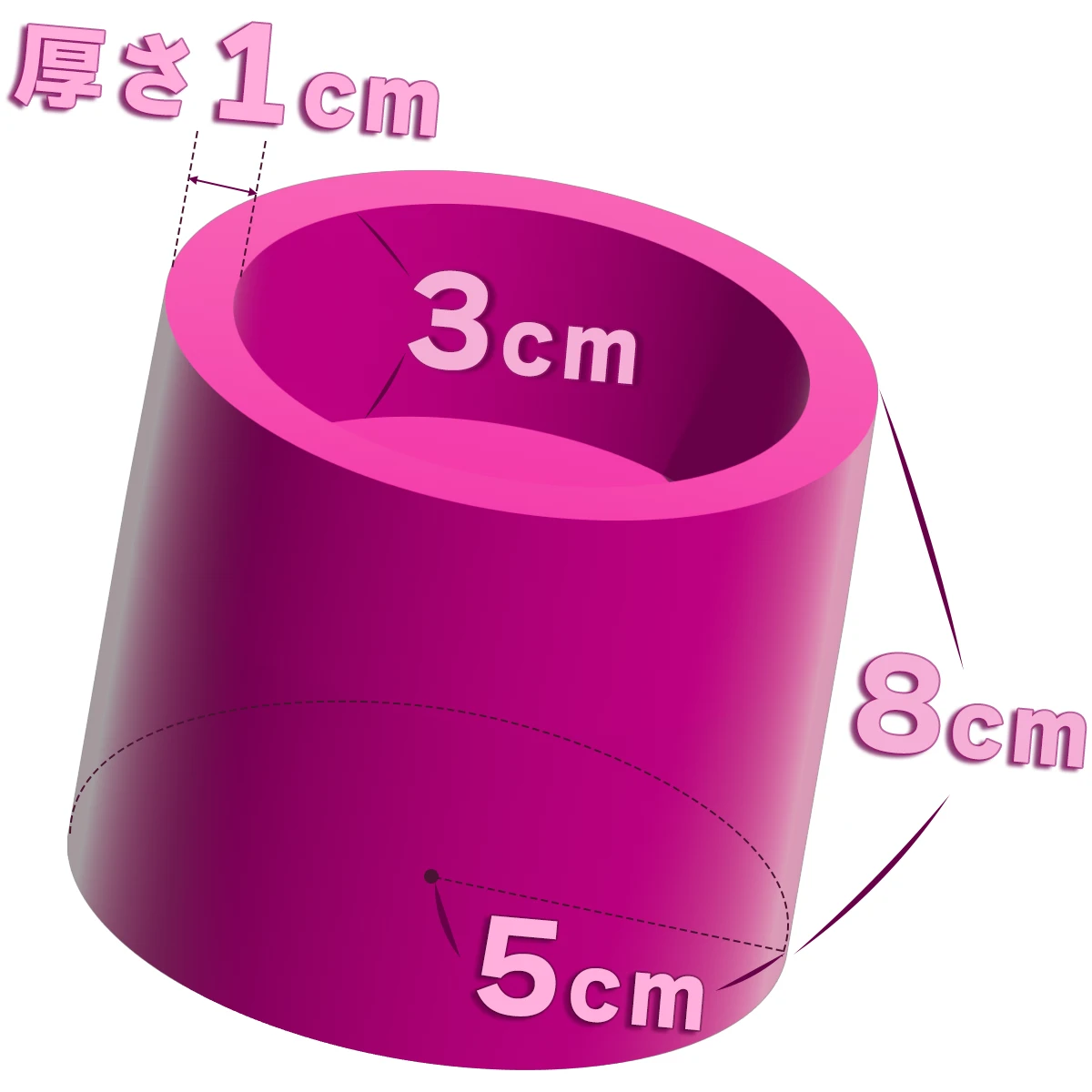
答え & 解説
- 477.28cm³
大きい円柱の体積から 小さい円柱の体積を引く
それぞれの体積は、
『 半径×半径×3.14×高さ 』 で
5×5×3.14×8 - 4×4×3.14×3 =
計算やってみる
\begin{eqnarray} 5 \times 5 \times 3.14 \times 8 - 4 \times 4 \times 14 \times 3 &=& \\[0.5em] 628-150.72 &=& 477.28 \\[0.5em] \end{eqnarray}
厚さ1cmの木材でマスを作った。外側のサイズは1辺8cmである。このマスの表面積を求めていただきたい!

答え & 解説
- 552cm²
ポイントは真上から見たとき
縁のところが計算めんどくさ・・

落ち着いて上から見るべし

!! 縁 と 内側の底を合わせたら、8×8の正方形の面積だ!! ついでに底を持ち上げてみると分かりやすい。
立方体の表面積と同じ
『8cm×8cm=64cm²』が6面あるっつーことで、
8×8×6=384

あとは内側の側面だけ

木材の厚さが1cmだから、内のりのサイズは7cmと6cmよね。
『7cm×6cm=42cm²』が4面あるっつーことで、
7×6×4=168
全部足すと、
384+168=552
このマスの表面積は 552cm² です!
とりあえずここまで~ 角柱と円柱でした
またちがうページでお会いしましょう!