四角形の種類と定義を楽しくおぼえる問題集

四角形の種類や関係をバッチリおぼえる無料の算数問題集です!
台形・平行四辺形・ひし形・長方形・正方形の関係を知ればもっと図形が得意になる~

四角形の定義だけさっさと知りたい人用
答えは□をクリック
ちょっと いきなり 問題出していいですか?
正方形は長方形でもある。○か×か
答えは□をクリック

正方形が長方形・・・???
このページを読めば 正方形は長方形でもあるってことが 分かるはずさ。
四角形の種類と関係を楽しくおぼえよ~!
↓この順番でやるのおすすめ↓

四角形のあれこれを楽しくおぼえたい人集合
問題を解きながら四角形の関係を知ることができる。台形・平行四辺形・ひし形・長方形・正方形の関係を知ればもっと図形が得意になる!
もくじ
- 四角形の種類と定義
定義は正義だ!
四角形とは何ですか。四角形の定義を答えよ。
答えは□をクリック
では、四角形に集まってもらおう
4本の直線で囲まれた形のみなさん、集まれ!
4本の直線で囲まれていれば四角形だから、ぜんぶ四角形だ。

ちょっと名札つけといて。名札
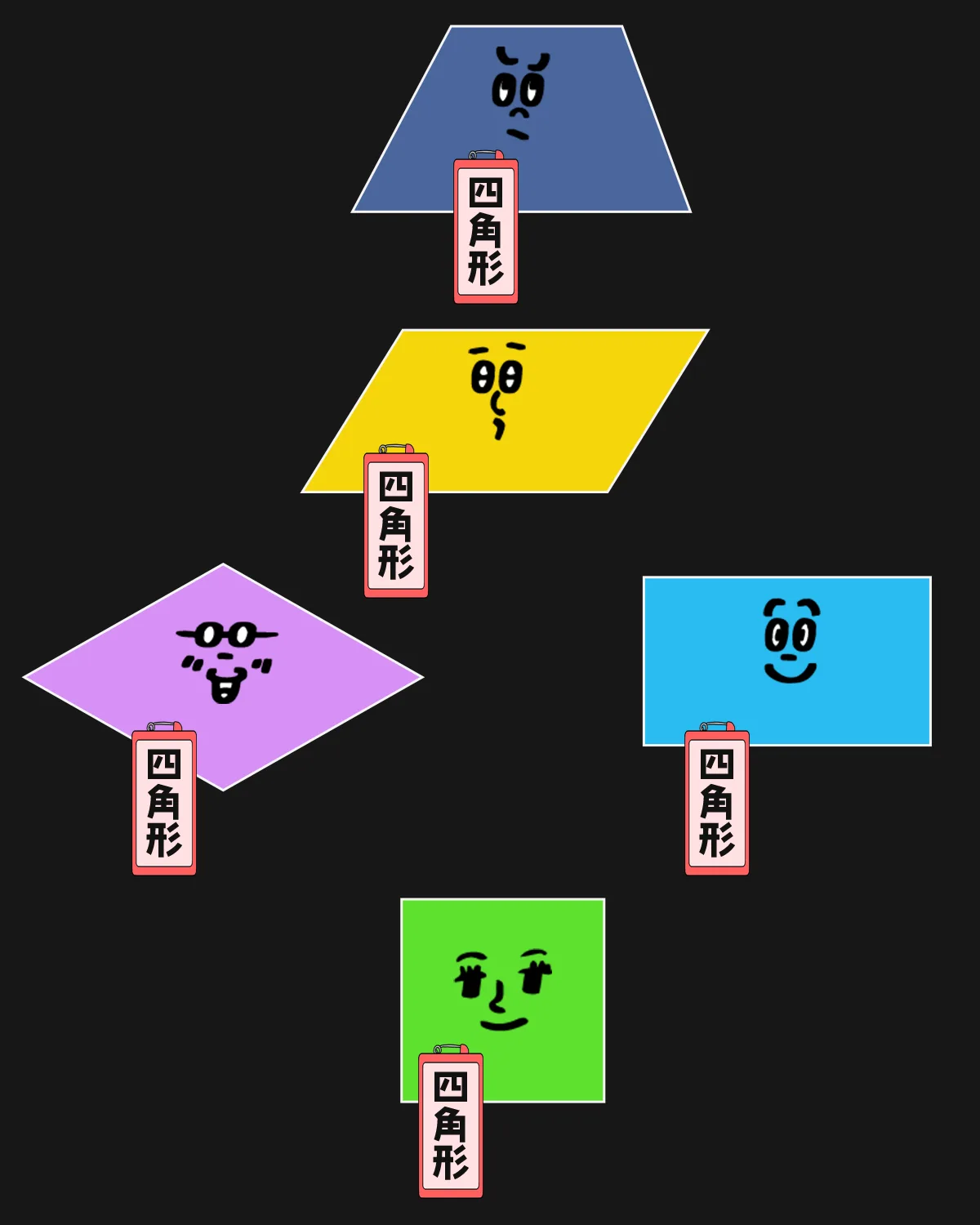
台形とは何ですか。台形の定義をバシッと答えよ。
では、台形に登場していただきましょう。
向かい合う1組の辺が平行な四角形さ~ん
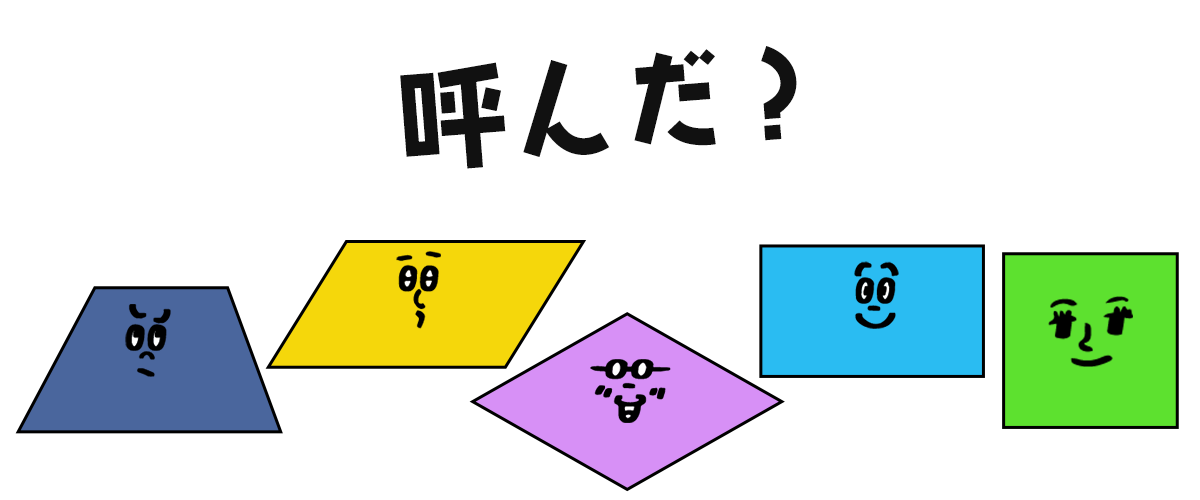
あれ? 全員来ちゃった。台形呼んだんですけど。台形じゃないのも来てるな・・

台形の定義をもうお忘れですか?
向かい合う1組の辺が平行な四角形・・ですよ
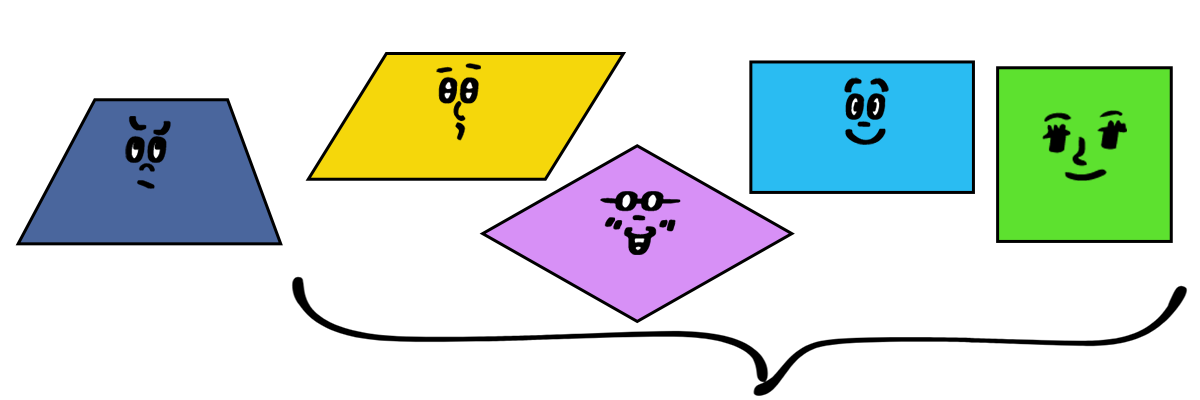
これらは 2組の辺が平行ですよね。ってことは、もちろん1組も平行です。だから、平行四辺形・ひし形・長方形・正方形も台形です。

名札つけとこ
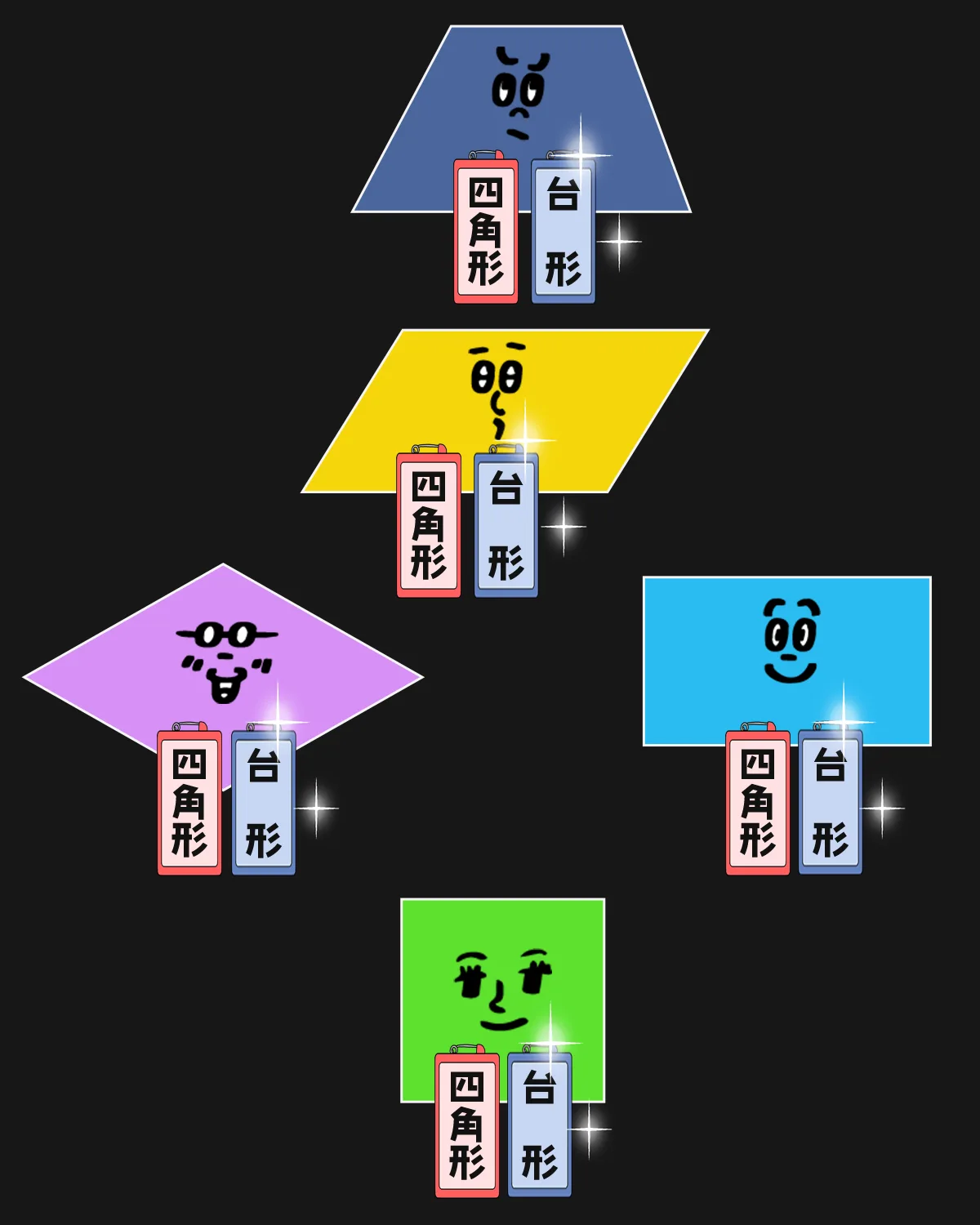

台形の定義は、「1組の辺だけが平行」 なんじゃなくて、「少なくとも向かい合う1組の辺が平行」ならOK
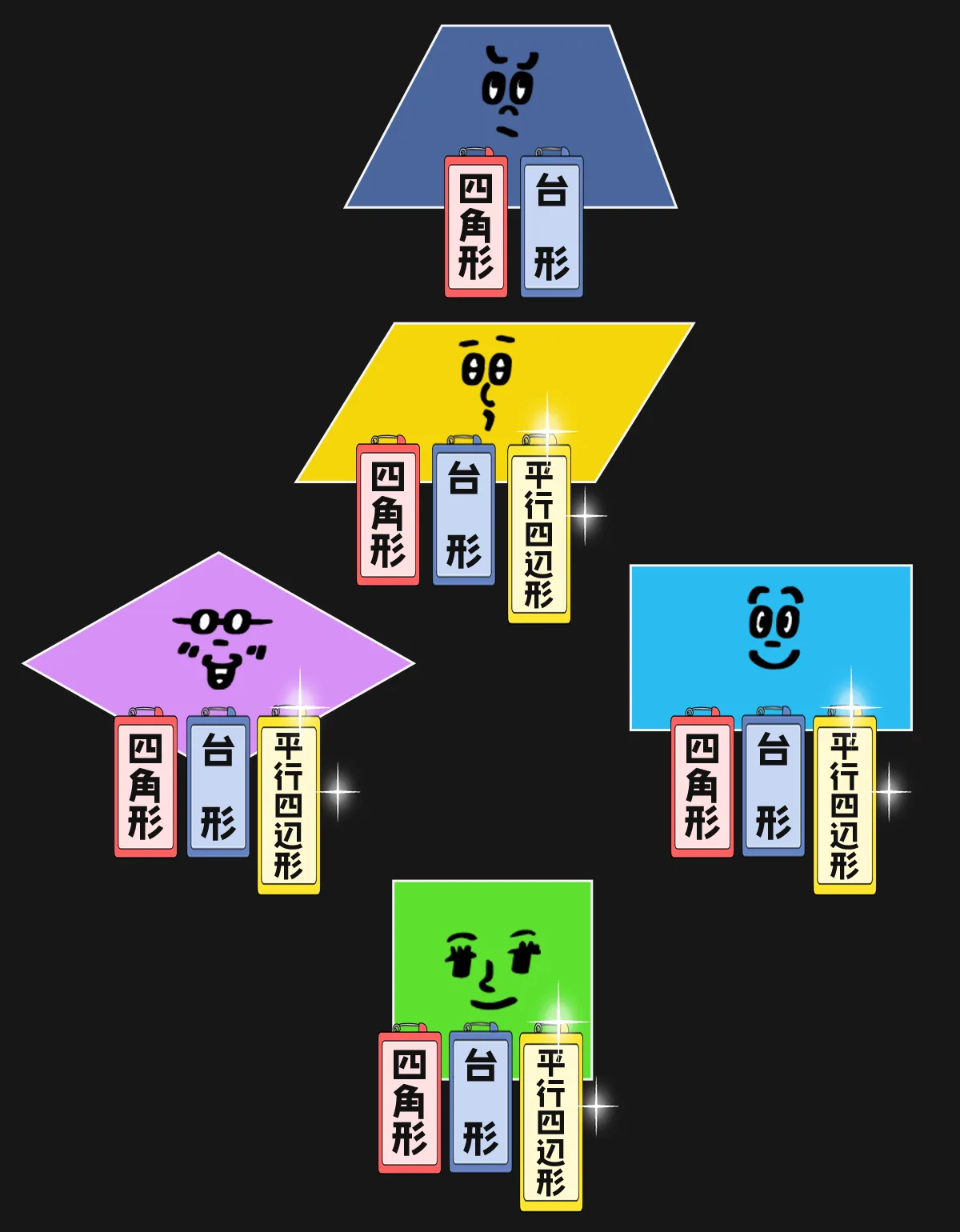
平行四辺形とは何ですか。平行四辺形の定義をズバッと答えよ。
では、平行四辺形の登場です。
向かい合う2組の辺が平行な四角形だけ!おいで~!
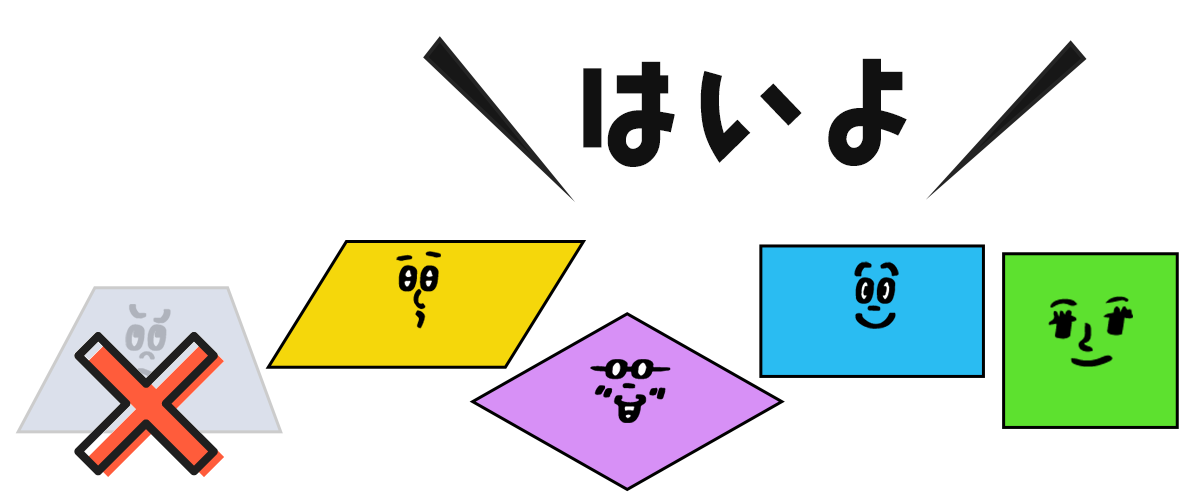
「はいよ」 じゃないのよ。ひし形とか長方形、正方形が 「はいよ」じゃないのよ。
そこの黄色いのが平行四辺形でしょ

また定義わすれたんか。
定義は絶対。
向かい合う2組の辺が平行な四角形は平行四辺形!
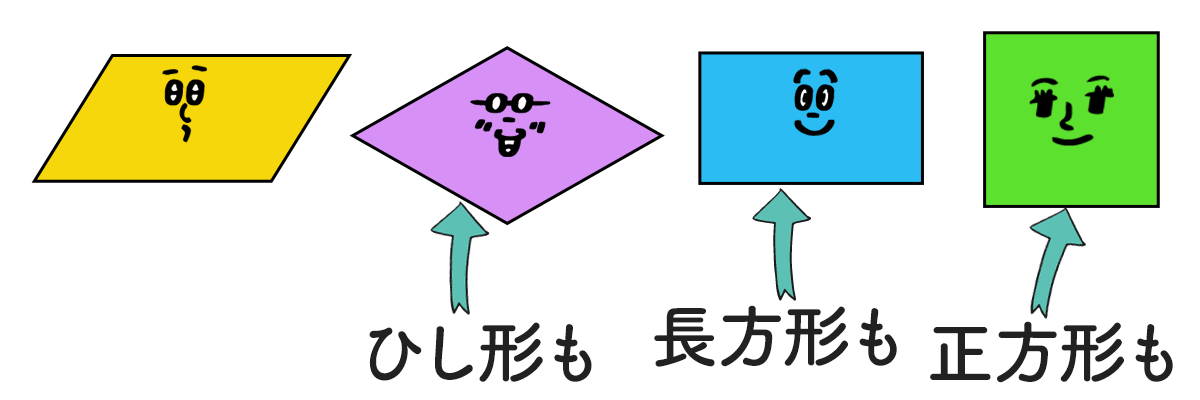
2組の辺が平行だわね。
2組の辺が平行だから、ひし形・長方形・正方形も平行四辺形です。

名札いっとこ
ひし形とは何ですか。ひし形の定義をバッチリ答えよ。
では、ひし形に来てもらいましょう。
すべての辺の長さが等しい四角形・・・すべての辺が等しい?!まさか、奴も来るんじゃ・・
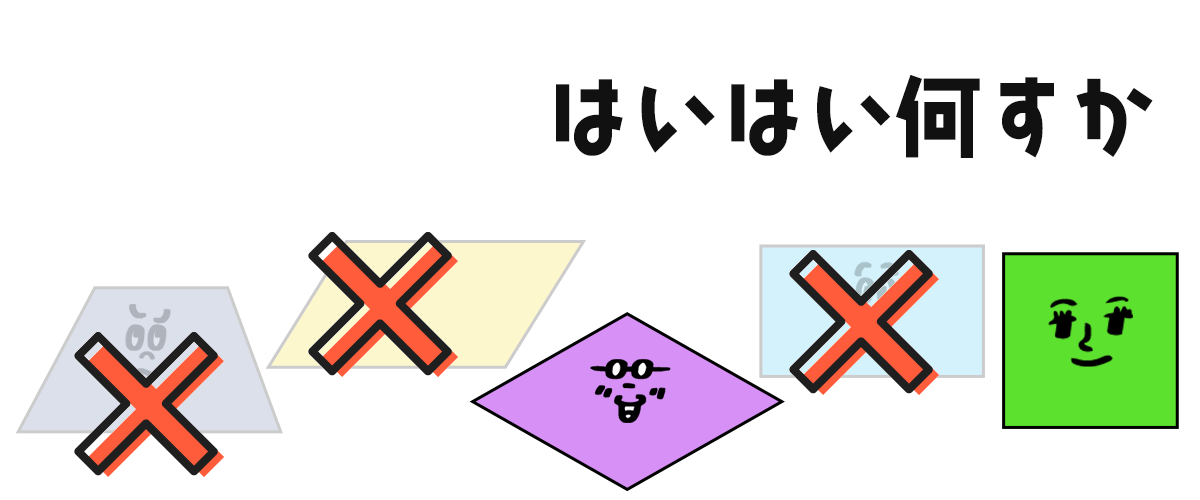
でた! 正方形! ひし形呼んだら正方形もきた!
もしかして、定義。。

定義は神
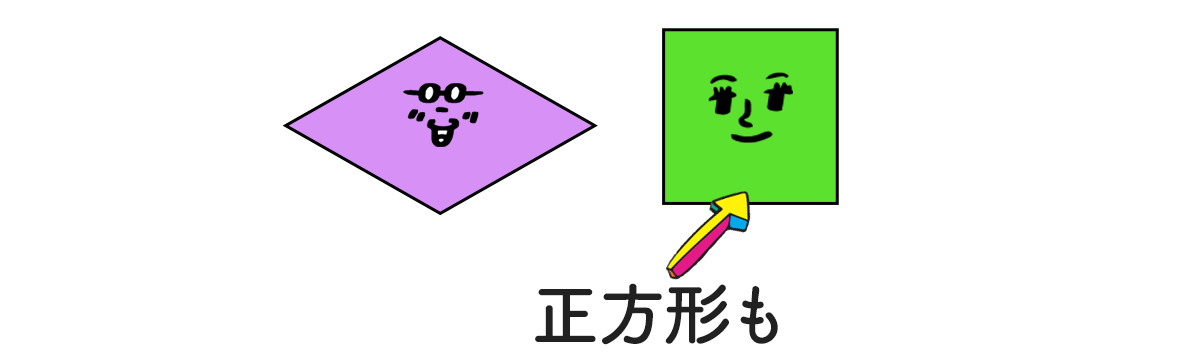
すべての辺の長さが等しい四角形はひし形!と定義されてる。
正方形もすべての辺が等しい四角形だから、ひし形でもある!
もっと言うと
ひし形の中でも 「すべての角が等しい(直角)」 っていう 特別な形が正方形。

では、ひし形と正方形に 新たな名札を
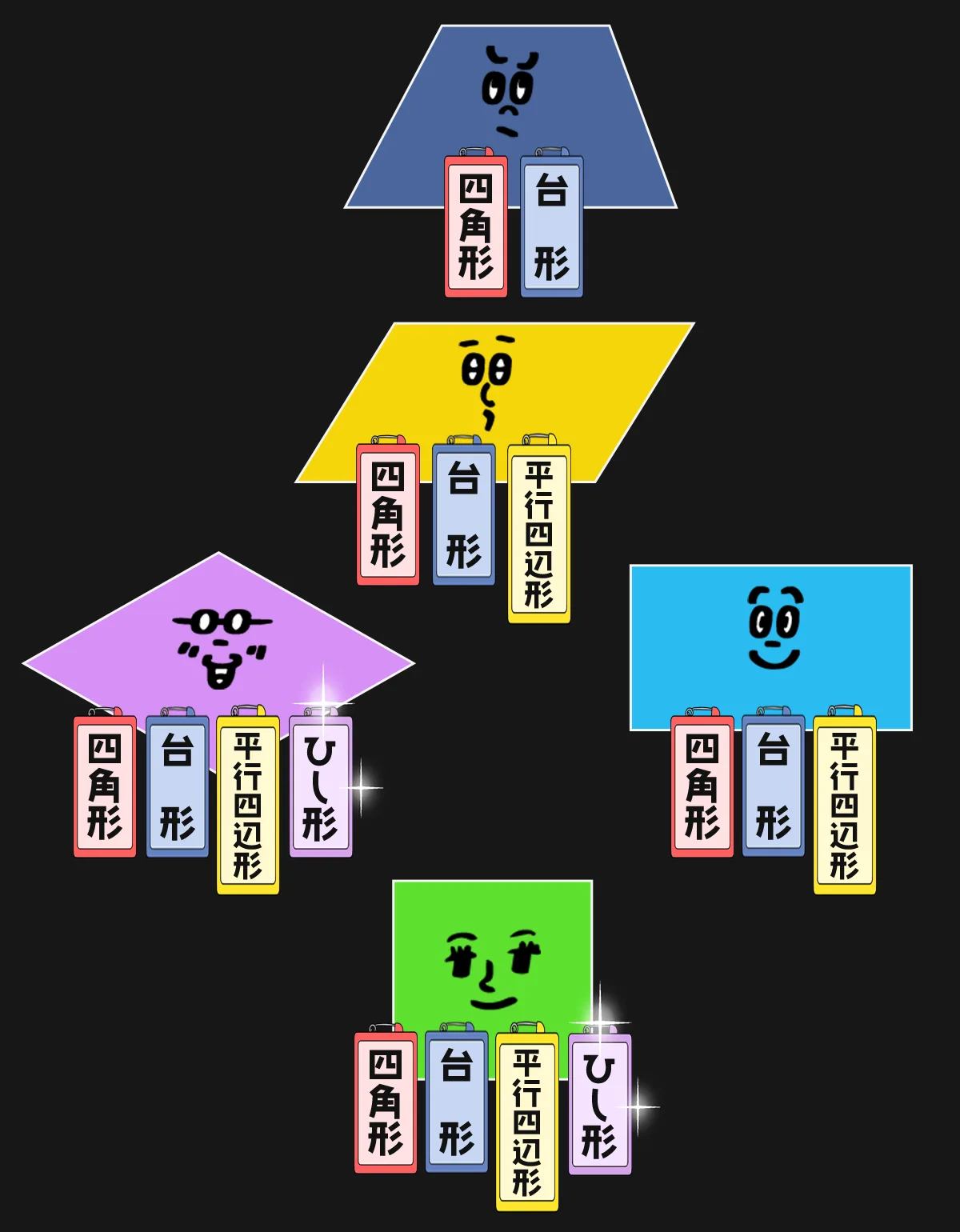
長方形とは何ですか。長方形の定義を答えちゃってください。
4つの角がすべて等しい四角形。4つの角がぜんぶ直角・・・
では呼びます。長方形~!
そうくると思ったけど、、正方形が長方形だなんて聞いたことない。

じゃあ今から聞いて♥
長方形か、長方形じゃないかは、4つの角がすべて等しい四角形なのか、そうじゃないかで決まる。
正方形も 4つの角がすべて等しいから 長方形でもあるのだ!
もっと言うと
長方形の中でも 「すべての辺の長さが等しい」 っていう 特別な形が正方形。

名札のお時間です
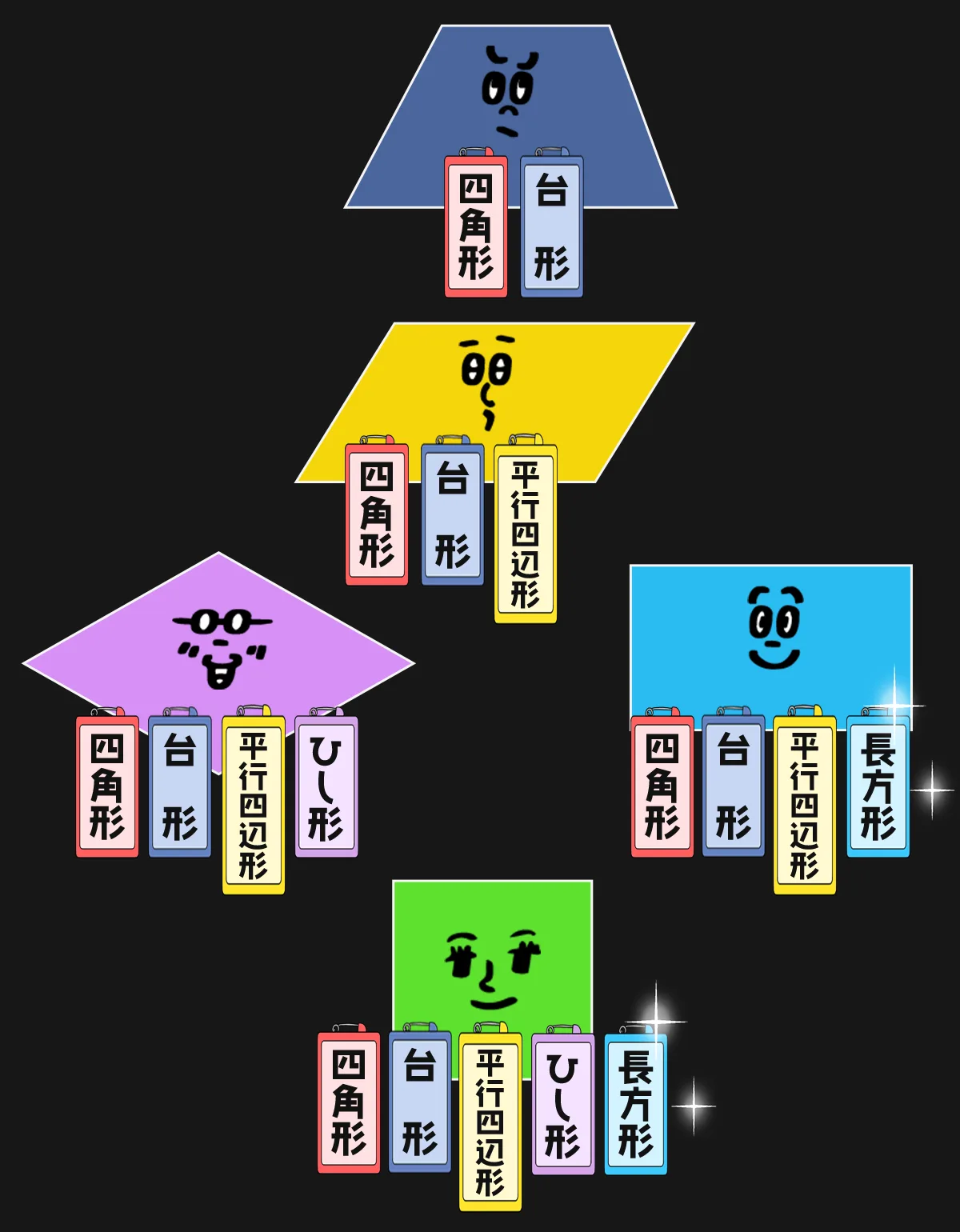
今のところ 正方形はすべての名札が付いてますね。めちゃくちゃスペック高いじゃないですか正方形。
正方形とは何ですか。正方形の定義を答えよ。
では、正方形の登場です。拍手でお迎えください。
4つの角がすべて等しい、そして辺の長さもすべて等しい四角形、いらっしゃ~い

超ウルトラ得意顔で登場っすね。手もあるんですか正方形って。※ないです
正方形の定義に当てはまるのは 正方形だけ!

最後の名札
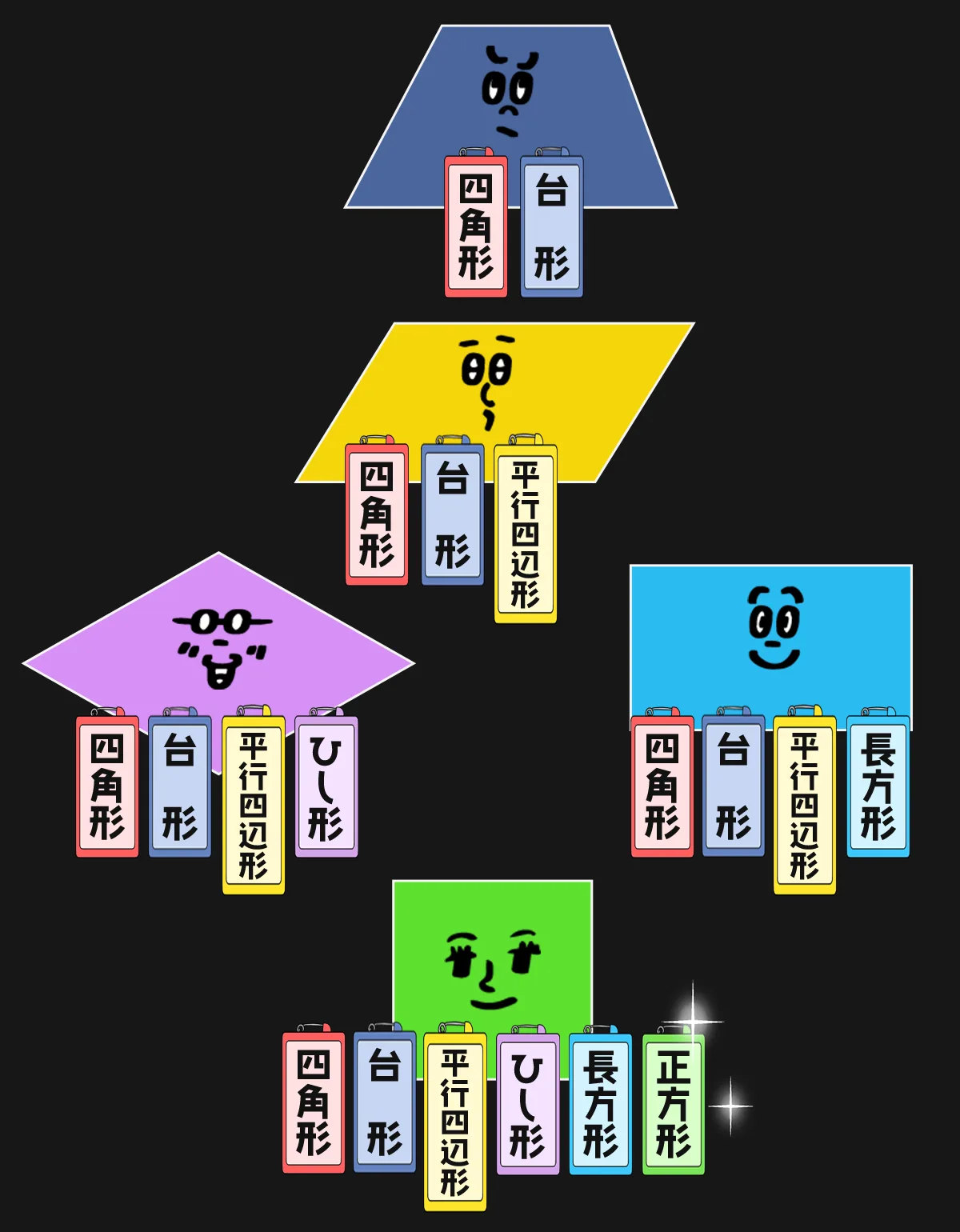

自分より上にある形の定義を引き継いでるのね
正方形は、これらの四角形の定義をぜ~んぶ持っているから、
台形でもあるし 平行四辺形でもあるし ひし形でもあるし 長方形でもある!
というスペシャルな形
ちょっとまて
ちょっとまて
ちょっとまて
じゃあ、「 台形をかきましょう 」って言われて平行四辺形をかいたり、「 長方形をかきましょう 」って言われて正方形をかいたりしても 間違いじゃないってことだな?
そうしちゃうぞ? いいんだな?

間違いではないよ。
でも落ち着いて
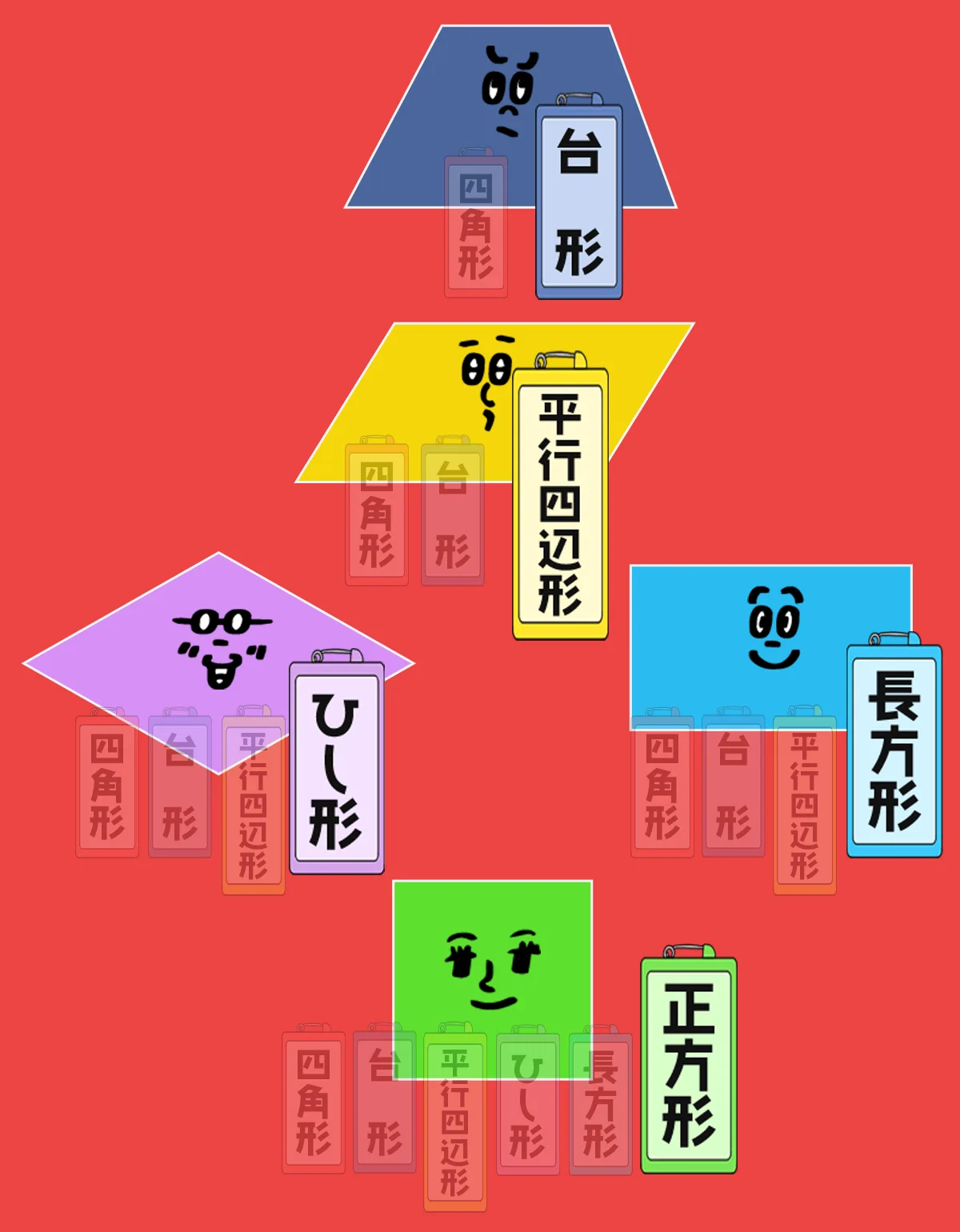
最後につけた名札が 代表的な名前ってことで、まあ基本はそっちを使おうよ。
「長方形をかいて」 って言ってる人は やっぱり代表的な長方形 ▭をかいてほしいと思ってるじゃない。
そこで

□
はい 長方形かいた
間違ってないけど ただの「へそまがり野郎」 みたいじゃん。
間違ってないけどね!
四角形の定義まとめます。
答えは□をクリック
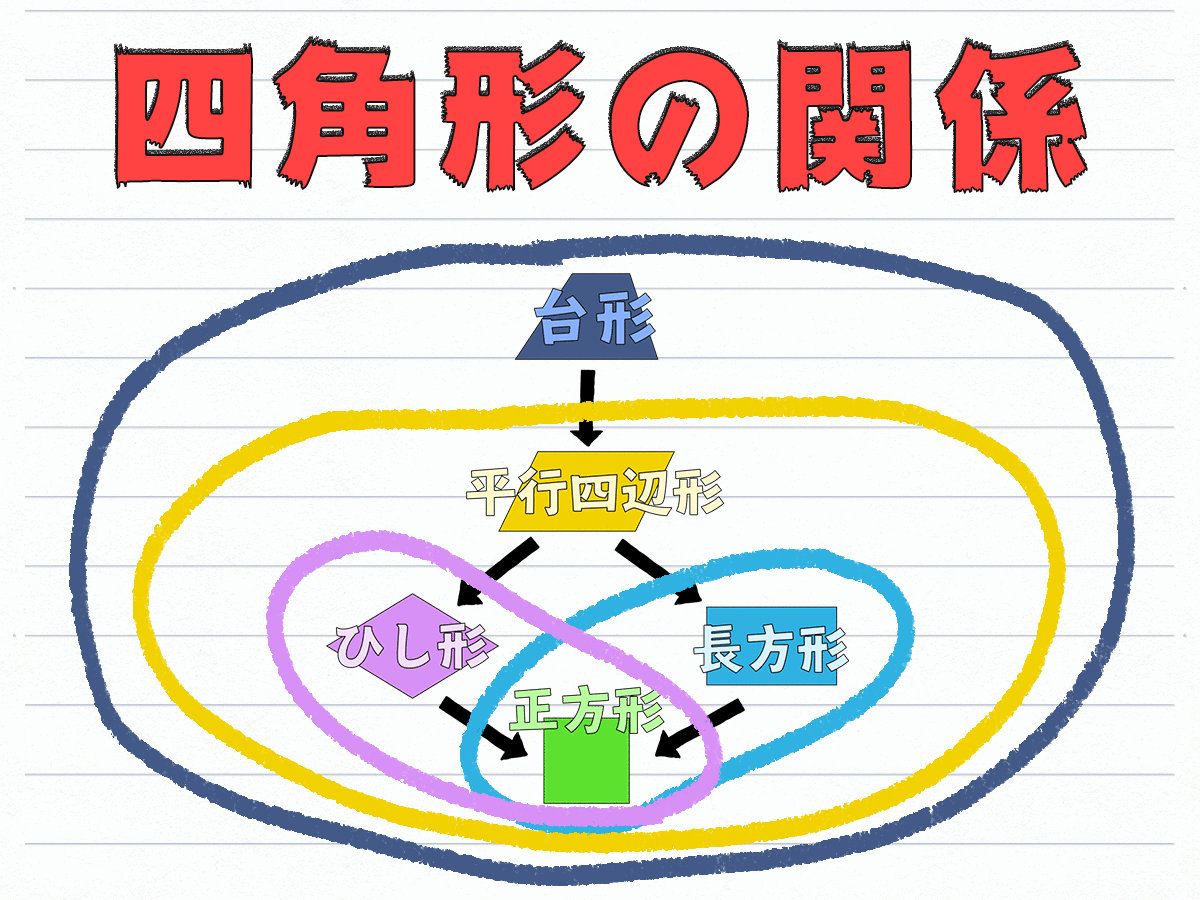
どこがどうなる?四角形の変形
じゃあ 次の図を見てもらおう。
四角形が矢印の順に変形していく図です。
台形から 最後の正方形になるまで 少しずつ変形してます。

この四角形たちは、つぎの形になるとき どう変形しているか。
問題!
台形が平行四辺形になるには、(1)~(4)のどれを行えばいいですか。

- すべての辺の長さを等しくする。
- 1組の辺の長さを等しくする。
- もう1組の辺を平行にする。
- 4つの角の大きさを等しくする。
答えをくわしく
台形は すでに1組の辺が平行だから、もう1組の辺を平行にすれば平行四辺形になる。
平行四辺形がひし形になるには、(1)~(4)のどれを行えばいいですか。

- すべての辺の長さを等しくする。
- 1組の辺の長さを等しくする。
- もう1組の辺を平行にする。
- 4つの角の大きさを等しくする。
答えをくわしく
すべての辺の長さが等しくないと ひし形じゃないから!
平行四辺形が長方形になるには、(1)~(4)のどれを行えばいいですか。

- すべての辺の長さを等しくする。
- 1組の辺の長さを等しくする。
- もう1組の辺を平行にする。
- 4つの角の大きさを等しくする。
ひし形が正方形になるには、(1)~(4)のどれを行えばいいですか。

- すべての辺の長さを等しくする。
- 1組の辺の長さを等しくする。
- もう1組の辺を平行にする。
- 4つの角の大きさを等しくする。
長方形が正方形になるには、(1)~(4)のどれを行えばいいですか。

- すべての辺の長さを等しくする。
- 1組の辺の長さを等しくする。
- もう1組の辺を平行にする。
- 4つの角の大きさを等しくする。
超ウルトラスーパーひっかけ問題
よくあるちょっといじわるな問題です。
ここまでやってきたことを思い出して解いてみてね~
4つの辺の長さが等しい四角形は何ですか。
~ ここから解説 ~
正方形って答えたくなるよね、これ。
でも 正解はひし形。
正方形って書くと×されたりすることもある問題なのよ
よくある声 パート1

いやいや、「4つの辺の長さが等しい」のは正方形もだよ。
だから答えは正方形でも 間違ってはないでしょ
まあたしかに、
正方形は4つの辺の長さが等しい四角形だ。だけど、
4つの辺の長さが等しい四角形といえば正方形 だけじゃない。ひし形がある!
よくある声 パート2

じゃあ ひし形って答えたら、正方形の立場はどうなる?
~ さあ思い出すのです ~
正方形はひし形でもある!
ひし形の中でも 「すべての角が等しい(直角)」 っていう 特別な形が正方形
ひし形って答えれば正方形も含まれてる。
逆に ひし形は正方形ではない。
なので 正方形って答えた場合、、

じゃあ ひし形は? ひし形は「4つの辺が等しい四角形」 でしょ! ひし形のこと無視したな! ひし形のこと忘れたか!あ~ひし形がかわいそう
こうなるかも。
ひし形は正方形も含んでるから、答えはひし形。
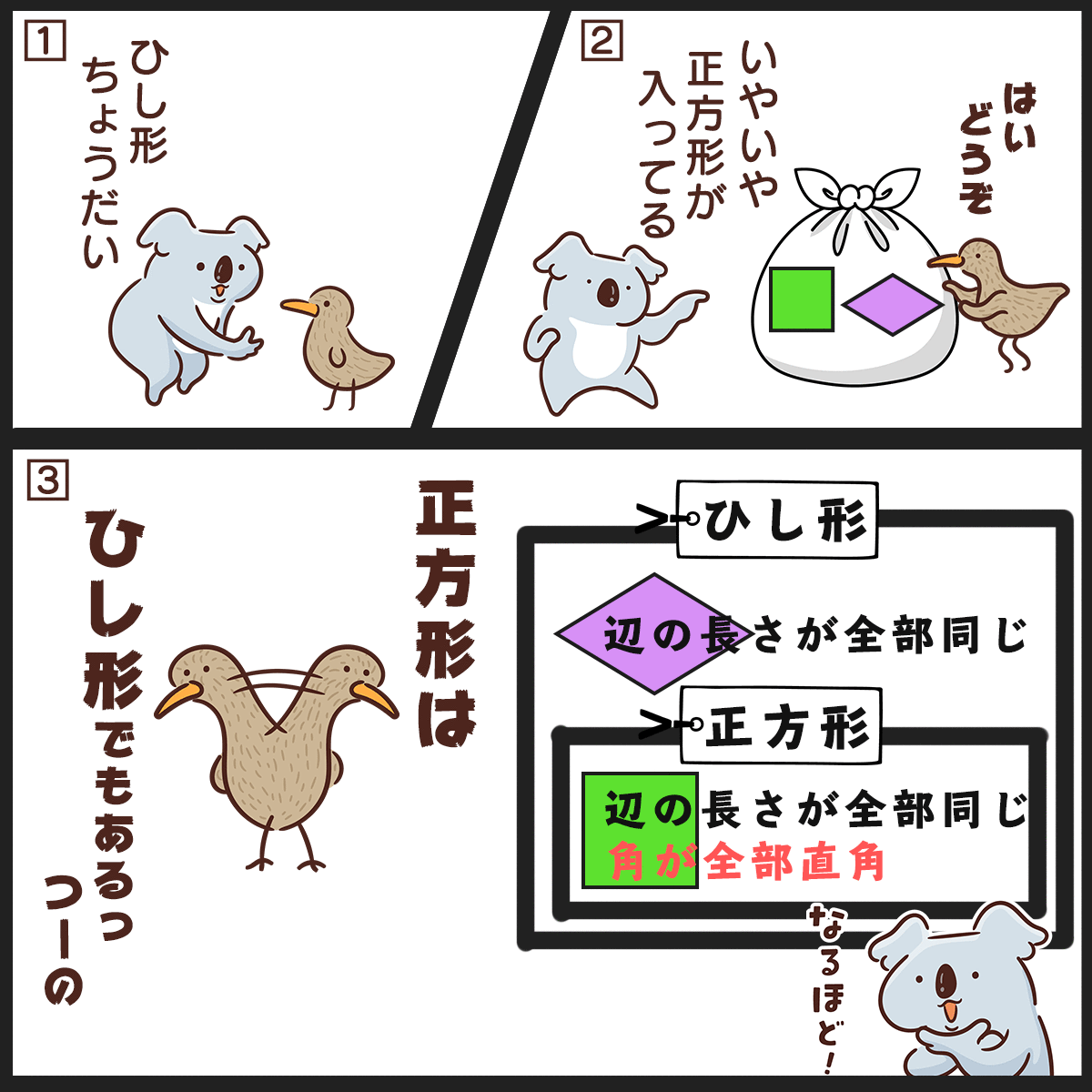
四角形の関係が さっきより分かったんじゃないかな~
でも1度にちゃんと理解するのはむずかしいかもしれないから、忘れたらまた見に来てね~!