5年生｢分数｣第1弾！
約分も通分もこれで完璧だ

5年生の分数、約分も通分もこれで完璧だ

5年生の分数、第1弾！約分(やくぶん)や通分(つうぶん)などをばっちり覚えられるページです。

約分、通分、分数と小数の関係、分数と割り算の関係などなど、分数いきまーす！

5年生の分数

同じ大きさの分数

あの～この3つの分数、、どう思います？

$ \dfrac{1}{2} $ $ \dfrac{2}{4} $ $ \dfrac{3}{6}$

$ \dfrac{1}{2} $ と $ \dfrac{2}{4} $ と $ \dfrac{3}{6}$

どうも思わないけど

なぬ？どうも思わない？

じゃあ図を見てよ

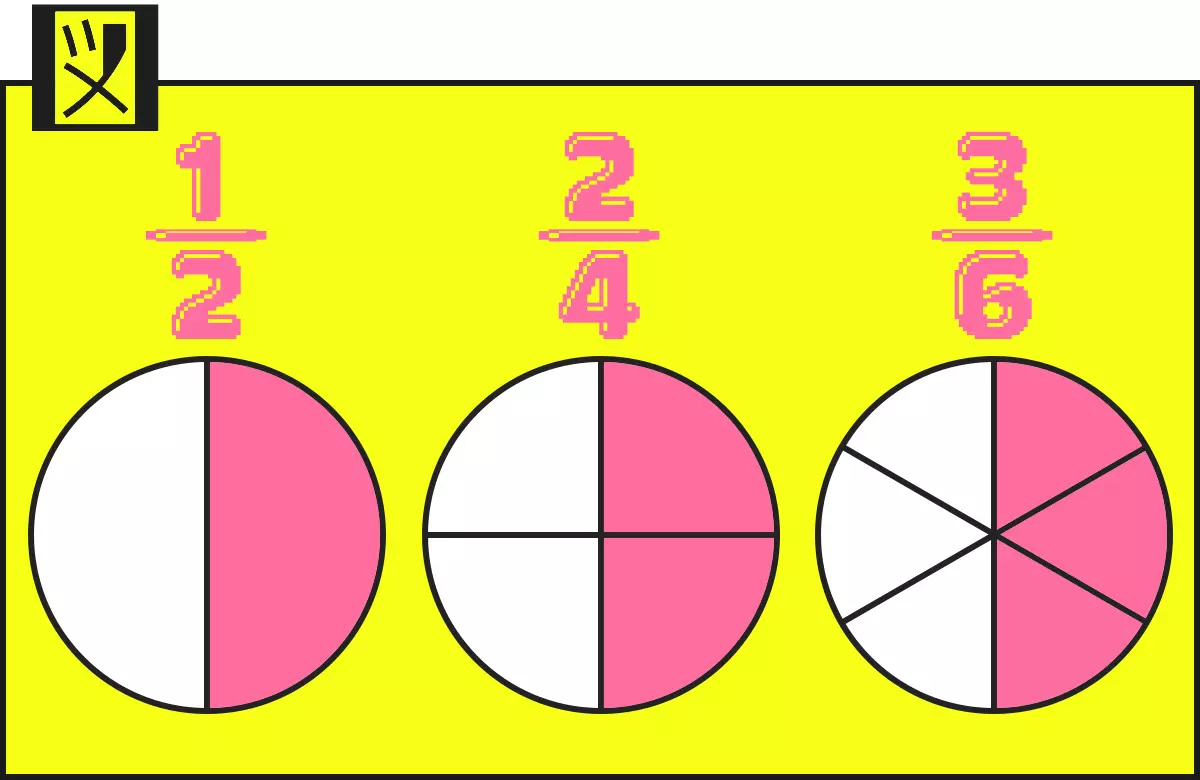
同じ大きさの分数

数字はちがうけど、大きさ同じ～～～！！

そういうこと。

$ \dfrac{1}{2} $ の分母と分子に 2をかけると

$ \dfrac{1^{ × 2 }}{2_{ × 2 }} = \dfrac{2}{4} $

$ \dfrac{1}{2} $ の分母と分子に 3をかけると

$ \dfrac{1^{ × 3 }}{2_{ × 3 }} = \dfrac{3}{6} $

分母と分子に同じ数をかけたり、同じ数で割ったりしても
分数の大きさは変わらない！

↑ 大事なんでもう一回読んで

つぎは、 $ \dfrac{1}{2} $ の分母と分子に 50をかけてみる

$ \dfrac{1^{ × 50 }}{2_{ × 50 }} = \dfrac{50}{100} $

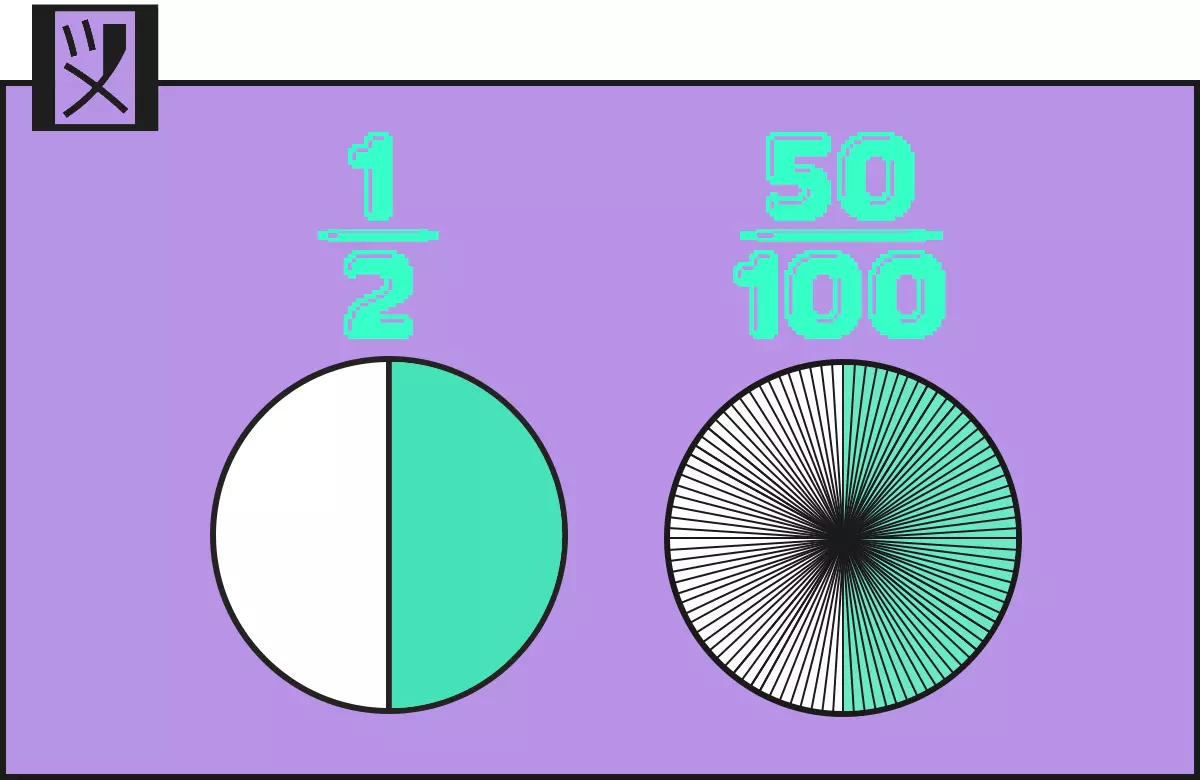
100分の50と2分の1は同じ大きさ

100に分けたら線が細かすぎて真ん中まっ黒になっちまった

まん中真っ黒に気を取られて、$ \dfrac{50}{100} $ も $ \dfrac{1}{2} $ だ！ってことが頭に入ってこない

それはごめんなさい。まあ、同じ大きさでしたってことで。

つぎは同じ数で割ってみる

$ \dfrac{3}{12} $ の分母と分子を同じ数で割る

いくつで割る？ 3で割る！

$ \dfrac{3^{ ÷ 3 }}{12_{ ÷ 3 }} = $ $ \dfrac{1}{4} $

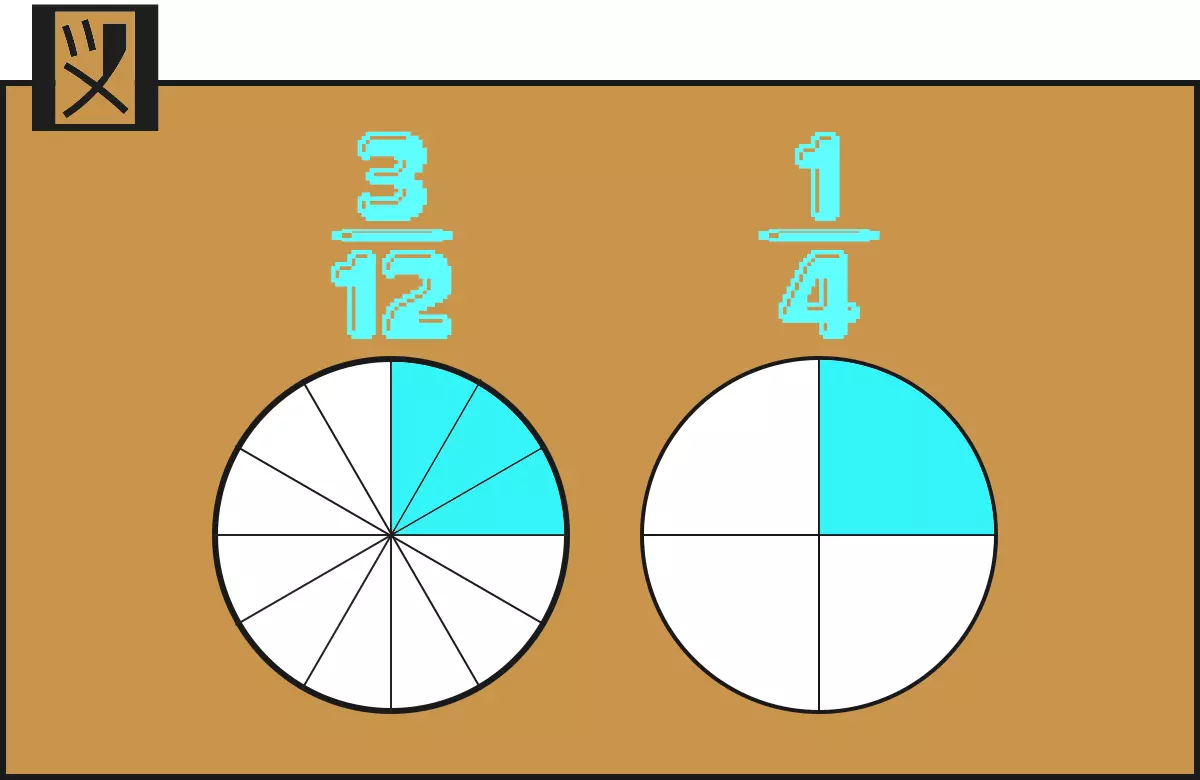
12分の3と4分の1は同じ大きさ

はい、大きさ同じ。

ということで、

分母と分子に同じ数をかけたり～、同じ数で割ったりしても～
分数の大きさは変わらない！

次の□にあてはまる数はなんでしょう。

$ \dfrac{\bbox[yellow, 1pt, border: 1px dotted red]{あ}}{3} = \dfrac{4}{6} = \dfrac{8}{\bbox[yellow, 1pt, border: 1px dotted red]{い}} $

あ 2 い 12

$ \dfrac{3}{4} = \dfrac{9}{\bbox[yellow, 1pt, border: 1px dotted blue]{あ}} = \dfrac{18}{\bbox[yellow, 1pt, border: 1px dotted blue]{い}} $

あ 12 い 24

$ \dfrac{3}{\bbox[yellow, 1pt, border: 1px dotted red]{あ}} = \dfrac{9}{15} = \dfrac{\bbox[yellow, 1pt, border: 1px dotted red]{い}}{20} $

あ 5 い 12

$ \dfrac{\bbox[yellow, 1pt, border: 1px dotted blue]{あ}}{2} = 2 = \dfrac{16}{\bbox[yellow, 1pt, border: 1px dotted blue]{い}} $

あ 4 い 8

$ 3 = \dfrac{\bbox[yellow, 1pt, border: 1px dotted red]{あ}}{3} = \dfrac{18}{\bbox[yellow, 1pt, border: 1px dotted red]{い}} $

あ 9 い 6

$ \dfrac{\bbox[yellow, 1pt, border: 1px dotted blue]{あ}}{4} = 4 = \dfrac{20}{\bbox[yellow, 1pt, border: 1px dotted blue]{い}} $

あ 16 い 5

$ \dfrac{\bbox[yellow, 1pt, border: 1px dotted red]{あ}}{7} = \dfrac{20}{28} = \dfrac{60}{\bbox[yellow, 1pt, border: 1px dotted red]{い}} $

あ 5 い 84

$ 2\dfrac{1}{4} = 2\dfrac{2}{\bbox[yellow, 1pt, border: 1px dotted blue]{あ}} = \dfrac{\bbox[yellow, 1pt, border: 1px dotted blue]{い}}{4} $

あ 8 い 9

$ 1\dfrac{\bbox[yellow, 1pt, border: 1px dotted red]{あ}}{7} = \dfrac{12}{21} = \dfrac{\bbox[yellow, 1pt, border: 1px dotted red]{い}}{7} $

あ 4 い 11

$ 3\dfrac{\bbox[yellow, 1pt, border: 1px dotted red]{あ}}{8} = 3\dfrac{6}{16} = \dfrac{\bbox[yellow, 1pt, border: 1px dotted blue]{い}}{8} $

あ 3 い 27

約分してスッキリ！

さっき $ \dfrac{3}{12} $ の分母＆分子を3で割って $ \dfrac{1}{4} $にした。

こんなふうに、分数の分母と分子を同じ数で割って、できるだけ小さい数にすることを約分(やくぶん) という。

$ \dfrac{3}{12} $ より $ \dfrac{1}{4} $のほうがシンプルで分かりやすいよね

ここで問題！

$ \dfrac{4}{12} $を約分するぞ。下の文の□をうめてくれ～

$ \dfrac{4}{12} $ の分母と分子を4で割ると $ \dfrac{1}{3} $

$ \dfrac{4}{12} $ を2で割ると $ \dfrac{2}{6} $ だ。まだ2で割れそうだから割ってみると $ \dfrac{1}{3} $ になる。

(2)みたいに少しずつ割っていくのもあり！ただ面倒(めんどう)だから、できるだけ大きい数で割った方がイイ

次の数をスッキリさせたい！約分お願いします

$ \dfrac{2}{8} $ $ \dfrac{1}{4} $ (÷2)
$ \dfrac{4}{12} $ $ \dfrac{1}{3} $ (÷4)
$ \dfrac{3}{15} $ $ \dfrac{1}{5} $ (÷3)
$ \dfrac{14}{21} $ $ \dfrac{2}{3} $ (÷7)
$ \dfrac{6}{10} $ $ \dfrac{3}{5} $ (÷2)
$ \dfrac{5}{40} $ $ \dfrac{1}{8} $ (÷5)
$ \dfrac{12}{16} $ $ \dfrac{3}{4} $ (÷4)
$ \dfrac{20}{25} $ $ \dfrac{4}{5} $ (÷5)
$ \dfrac{12}{33} $ $ \dfrac{4}{11} $ (÷3)
$ \dfrac{24}{40} $ $ \dfrac{3}{5} $ (÷8)
$ \dfrac{4}{14} $ $ \dfrac{2}{7} $ (÷2)
$ \dfrac{9}{36} $ $ \dfrac{1}{4} $ (÷9)
$ \dfrac{14}{35} $ $ \dfrac{2}{5} $ (÷7)
$ \dfrac{13}{52} $ $ \dfrac{1}{4} $ (÷13)
$ \dfrac{36}{63} $ $ \dfrac{4}{7} $ (÷9)
$ \dfrac{10}{100} $ $ \dfrac{1}{10} $ (÷10)
$ \dfrac{8}{20} $ $ \dfrac{2}{5} $ (÷4)
$ \dfrac{12}{24} $ $ \dfrac{1}{2} $ (÷12)
$ \dfrac{27}{54} $ $ \dfrac{1}{2} $ (÷27)
$ \dfrac{27}{57} $ $ \dfrac{9}{19} $ (÷3)
$ \dfrac{30}{42} $ $ \dfrac{5}{7} $ (÷6)
$ \dfrac{42}{54} $ $ \dfrac{7}{9} $ (÷6)
$ \dfrac{45}{54} $ $ \dfrac{5}{6} $ (÷9)
$ \dfrac{14}{49} $ $ \dfrac{2}{7} $ (÷7)
$ \dfrac{17}{51} $ $ \dfrac{1}{3} $ (÷17)

通分のやり方

先に言っちゃう。通分(つうぶん)とは何かを2回言っちゃう。

通分とは、分母をそろえること。
通分とは、分母をそろえること。

分母そろえてどうすんの？マジで必要なんすか？

必要なんすよ

↓足し算とか引き算で、分母がちがうと↓

$ \dfrac{1}{4} + \dfrac{2}{3} =$

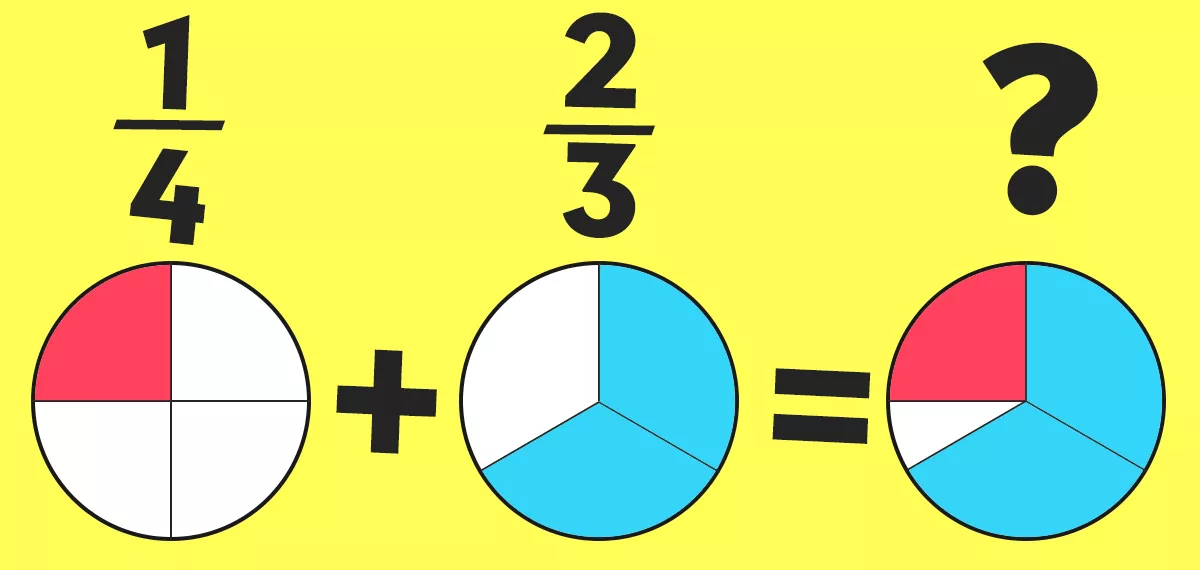
通分する前の分数の足し算

はい、計算できなーい。

分母がそろってないと、分数の足し算と引き算は激ムズ

さあ、分母をそろえるのです
そう、通分するのです

先に答えを見せる

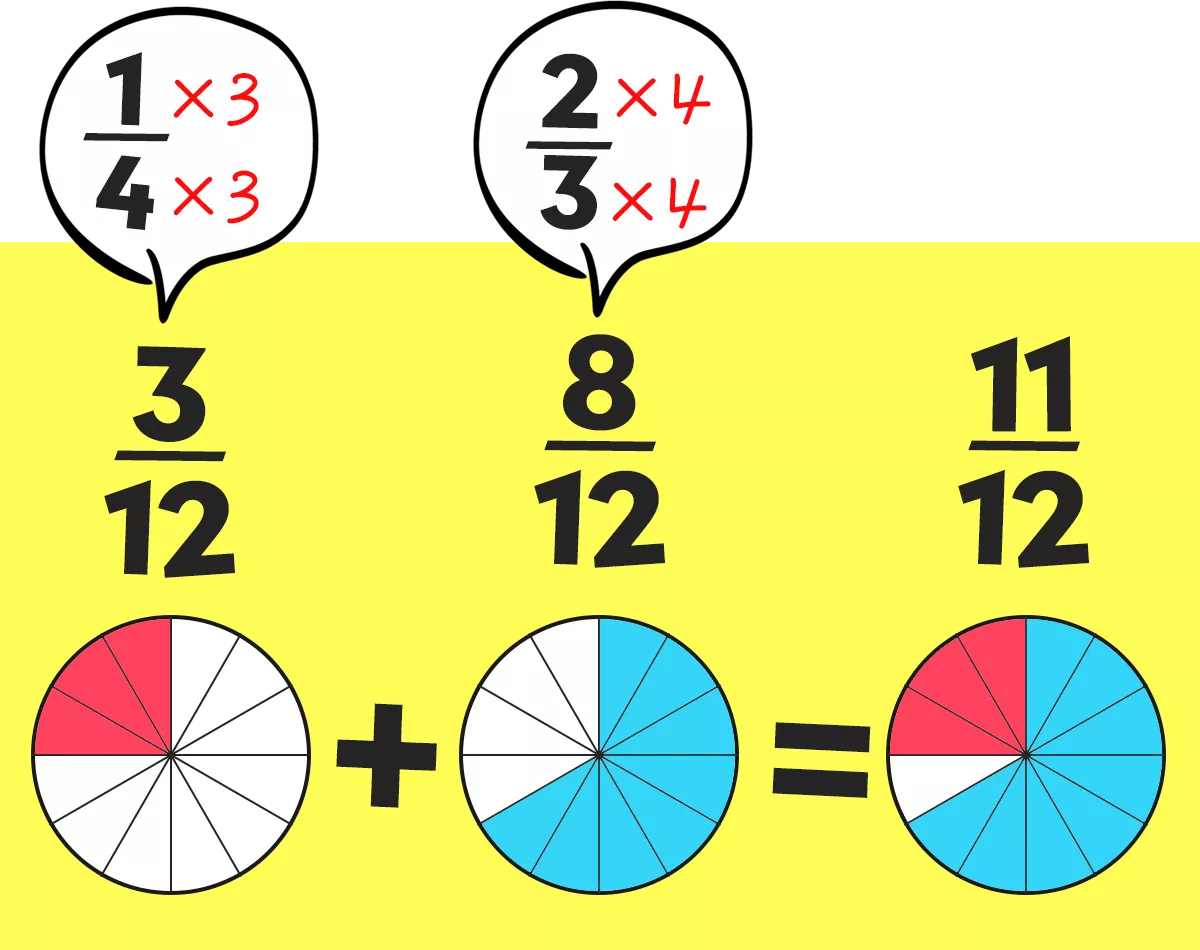
通分をした分数の足し算

$ \dfrac{1}{4} $ を $ \dfrac{3}{12} $ に

$ \dfrac{2}{3} $ を $ \dfrac{8}{12} $ に

分母をそろえることで足し算・引き算ができる。

どっちも、数字は変わったけど分数の大きさは変わってない！

～通分のやり方～

通分とは分母をそろえること

分母をそろえたい！

4と3の最小公倍数を見つけよう。

通分は分母の最小公倍数を探す

最小公倍数は12だ！

じゃあ、分母を12にそろえりゃいい

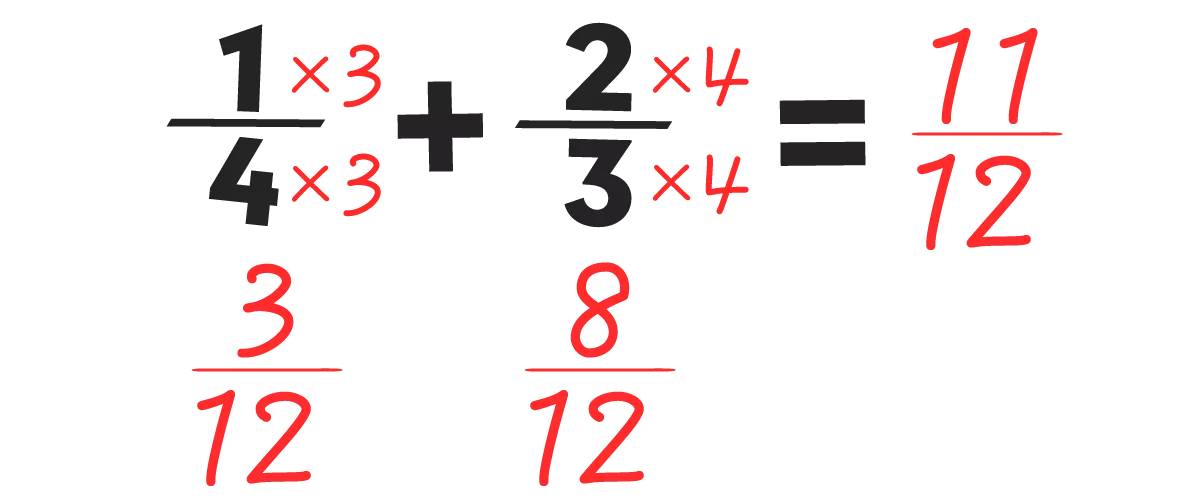
通分のしかた

分母と分子に同じ数をかければ分数の大きさは変わらないから
分子にも同じ数をかけてやる。
これは絶対！
これが通分！

通分これどうする？

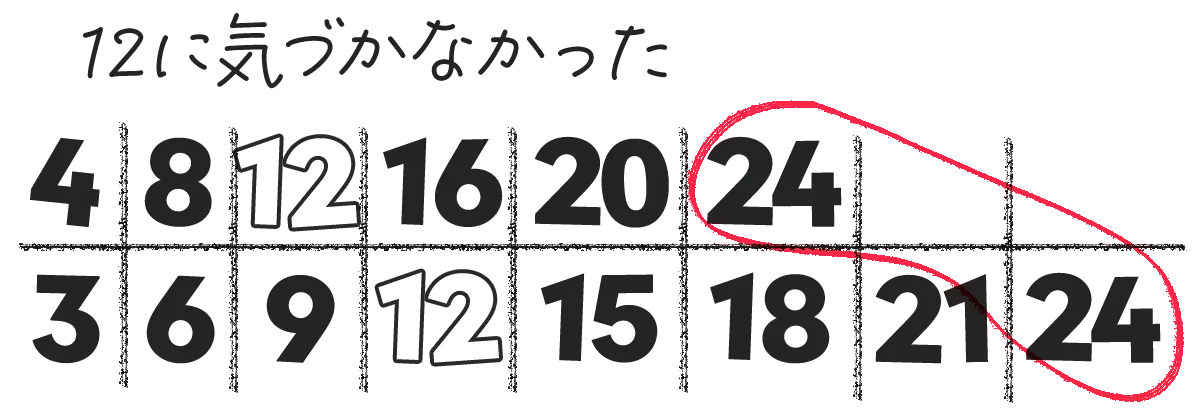
通分で最小公倍数ではない場合

最小公倍数の「12」に気づけなかったらどうなる？

よくあることさ

$ \dfrac{1}{4} + \dfrac{2}{3} = $

分母を「24」にするのね

$ \dfrac{1^{ × 6 }}{4_{ × 6 }} $ + $ \dfrac{2^{ × 8 }}{3_{ × 8 }} $ =

$ \dfrac{6}{24} + $ $ \dfrac{16}{24} $ = $ \dfrac{22}{24} $

で、答えを約分する！

$\frac{\cancel{22}}{\cancel{24}} \frac{11}{12} $

計算はできるってことね。

最小公倍数見つけた方が早いけど

つぎの分数を通分せよ～

$ \dfrac{1}{3} , \dfrac{3}{4} $ $ \dfrac{4}{12} , \dfrac{9}{12} $
$ \dfrac{4}{5} , \dfrac{1}{2} $ $ \dfrac{8}{10} , \dfrac{5}{10} $
$ \dfrac{3}{7} , \dfrac{1}{14} $ $ \dfrac{6}{14} , \dfrac{1}{14} $
$ \dfrac{2}{3} , \dfrac{2}{5} $ $ \dfrac{10}{15} , \dfrac{6}{15} $
$ \dfrac{1}{4} , \dfrac{1}{2} $ $ \dfrac{1}{4} , \dfrac{2}{4} $
$ \dfrac{5}{6} , \dfrac{3}{5} $ $ \dfrac{25}{30} , \dfrac{18}{30} $
$ \dfrac{2}{7} , \dfrac{5}{8} $ $ \dfrac{16}{56} , \dfrac{35}{56} $
$ \dfrac{4}{9} , \dfrac{5}{27} $ $ \dfrac{12}{27} , \dfrac{5}{27} $
$ \dfrac{5}{6} , \dfrac{1}{10} $ $ \dfrac{50}{60} , \dfrac{6}{60} $
$ \dfrac{2}{9} , \dfrac{3}{15} $ $ \dfrac{10}{45} , \dfrac{9}{45} $
$ \dfrac{3}{16} , \dfrac{3}{20} $ $ \dfrac{15}{80} , \dfrac{12}{80} $
$ \dfrac{1}{2} , \dfrac{2}{3} , \dfrac{1}{6} $ $ \dfrac{3}{6} , \dfrac{4}{6} , \dfrac{1}{6} $
$ \dfrac{5}{6} , \dfrac{2}{9} , \dfrac{5}{18} $ $ \dfrac{15}{18} , \dfrac{4}{18} , \dfrac{5}{18} $
$ \dfrac{1}{3} , \dfrac{3}{4} , \dfrac{1}{6} $ $ \dfrac{4}{12} , \dfrac{9}{12} , \dfrac{2}{12} $
$ \dfrac{3}{8} , \dfrac{2}{5} , \dfrac{7}{10} $ $ \dfrac{15}{40} , \dfrac{16}{40} , \dfrac{28}{40} $
$ \dfrac{1}{4} , \dfrac{2}{5} , \dfrac{5}{12} $ $ \dfrac{15}{60} , \dfrac{24}{60} , \dfrac{25}{60} $

小数を分数にする方法
分数を小数にする方法

分数と小数の関係図

少数を分数にする、分数を小数にする

簡単にサクッとできま～す。まずは、

小数を分数にする方法

とりあえずやってみましょう。答えは□をクリック

0.7 $ \dfrac{7}{10} $
0.5 $ \dfrac{\cancel{5}}{\cancel{10}} $ 約分して$ \dfrac{1}{2} $
1.7 $ \dfrac{17}{10} $または $ 1\dfrac{7}{10} $
0.03 $ \dfrac{3}{100} $
0.33 $ \dfrac{33}{100} $
1.33 $ \dfrac{133}{100} $または $ 1\dfrac{33}{100} $

分母が 10、100、1000とかになるのね。

じゃあ、分母が10なのか、100なのか、1000なのか何なのか分かればいい

小数の位っておぼえてる？

小数の位は2種類の言い方がある

そう、$ \dfrac{1}{10} $の位、$ \dfrac{1}{100} $の位、$ \dfrac{1}{1000} $の位とかいう。

0.261を分数にする

小数部分は$ \dfrac{1}{1000} $の位まであるから、分母は1000

0.261 = $ \dfrac{261}{1000} $

約分できないからこれでOK！

分子はそのまま261ね

そうです。分子はそのまま

103.261 だったら、$ \dfrac{103261}{1000} $

まあ帯分数だと、$ 103\dfrac{261}{1000} $ だけど

0.19を分数にする

小数部分は$ \dfrac{1}{100} $の位まであるから、分母は100

0.19 = $ \dfrac{19}{100} $

2.9を分数にする

小数部分は$ \dfrac{1}{10} $の位まであるから、分母は10

仮分数だと、2.9 = $ \dfrac{29}{10} $

帯分数だと、2.9 = $ 2\dfrac{9}{10} $

仮分数にするのか、帯分数にするのか、どっちがいいかはっきりしてくれない？

はい！出ました！
仮分数と帯分数どっちがいいのか！

どっちでもいい！

「帯分数で答えなさい」とか指示がなければ、どっちでもいい。

ただ、小学校では帯分数の出番が多い。

足し算、引き算のとき答えが仮分数になったら帯分数に直したりさ。

でも帯分数を使うのは小学生まで。

中学とかでこれからいろんな計算をするときは、ほぼ仮分数。

いや、ぜんぶ仮分数。

「これから帯分数はあまり使わないから、今のうちにがっつり使って理解しておこう！」

って感じですかね。

帯分数のいいところは、パッと分かりやすいとこ

クッキーが $ \dfrac{13}{4} $ 枚ある

よりも、

クッキーが $ 3\dfrac{1}{4} $ 枚ある

帯分数のほうが分かりやすくない？

仮分数から整数を取り出せる！ってことをはっきりさせるには、帯分数がいなきゃ始まんないし。

というわけで、指示がなければ帯分数でも仮分数でもどっちでもいい。

だけど、小学生は帯分数にしておくほうが安全。

小数を分数で表しちゃってください。

0.9 $ \dfrac{9}{10} $
0.07 $ \dfrac{7}{100} $
0.851 $ \dfrac{851}{1000} $
2.3 $ 2\dfrac{3}{10} $$\quad \left( \dfrac{23}{10} \right) $
13.41 $ 13\dfrac{41}{100} $$\quad \left( \dfrac{1341}{100} \right) $
1.01 $ 1\dfrac{1}{10} $$\quad \left( \dfrac{101}{100} \right) $
5 $ \dfrac{5}{1} $
7 $ \dfrac{7}{1} $
0.6 $ \dfrac{\cancel{6}}{\cancel{10}} $ 約分して$ \dfrac{3}{5} $
1.4 $ 1\dfrac{\cancel{4}}{\cancel{10}} $ 約分して$ \dfrac{2}{5} $
2.08 $ 2\dfrac{\cancel{8}}{\cancel{100}} $ 約分して$ 2\dfrac{2}{25} $

分数を小数にする方法

知ってるかもしれないけど

分数はわり算にできる

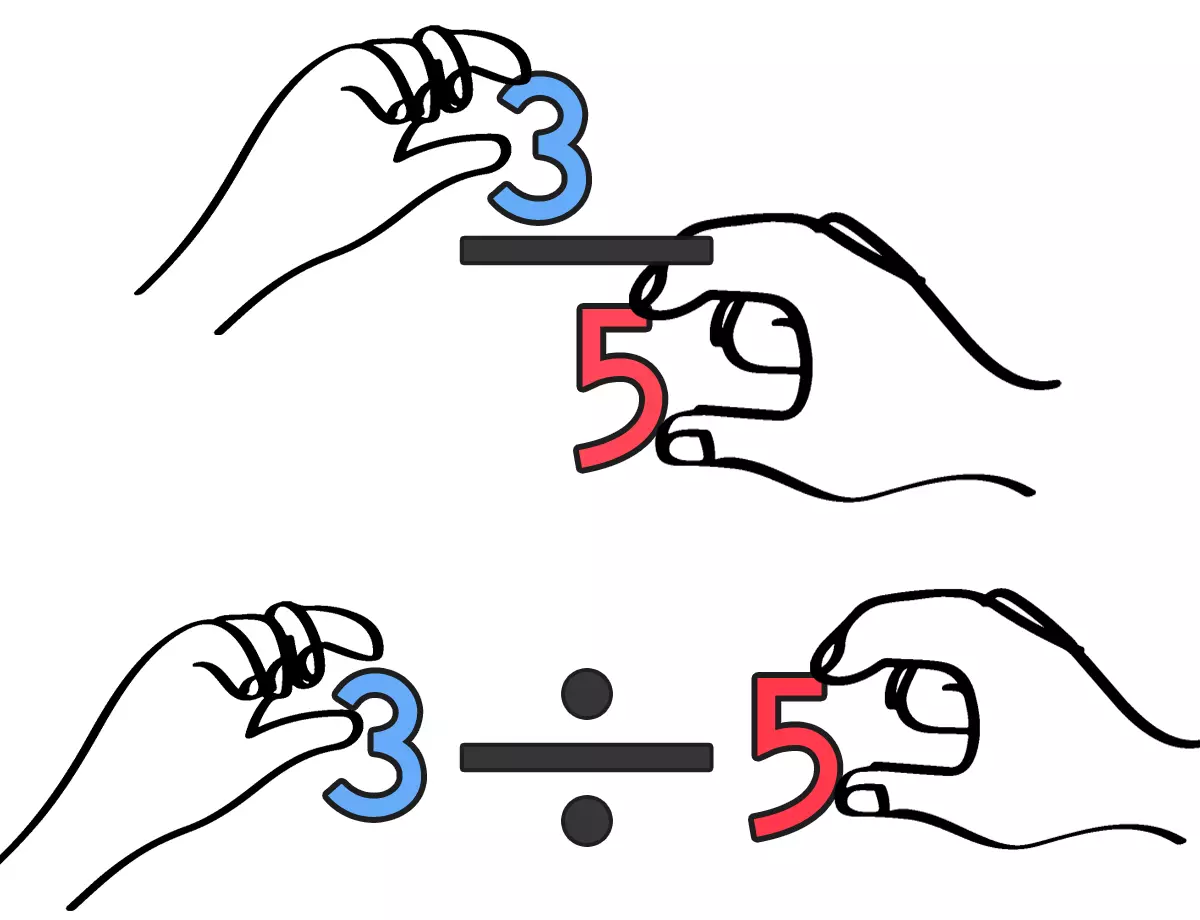
分子を割られる数、分母を割る数にする

分子÷分母

分子を割られる数、分母を割る数にする。

$ \dfrac{3}{5} = 3 \div 5 = 0.6 $

分数を割り算にすれば小数にできるわ！

ついでに帯分数バージョンやっとく？

$ 2\dfrac{3}{4} = \dfrac{11}{4}$

帯分数は仮分数にしてから

$ = 11 \div 4 = 2.75 $

つぎの分数を小数で表せ！

$ \dfrac{3}{10} $ 0.3
$ \dfrac{1}{4} $ 0.25
$ \dfrac{8}{25} $ 0.32
$ \dfrac{9}{5} $ 1.8
$ 2\dfrac{1}{4} $ 2.25
$ \dfrac{27}{50} $ 0.54
$ \dfrac{16}{25} $ 0.64
$ \dfrac{1}{8} $ 0.125

つぎの分数を小数で表してね。答えは四捨五入して$ \dfrac{1}{1000} $の位まで求めましょう。

$ \dfrac{1}{7} $ 0.143
0.1428まで計算しておく。$ \dfrac{1}{10000} $の位の「8」を四捨五入して $ \dfrac{1}{1000} $の位までを求めりゃOK!
$ \dfrac{7}{12} $ 0.583
$ 1\dfrac{1}{13} $ 2.077

割りきれない割り算も分数ならバシッと

たとえばこんな問題

2mのロープを3等分した１つ分の長さは何m？？

2mを3等分だから、

2÷3 = 0.66666･･･

割りきれない

そんな割りきれない割り算も！？
答えを分数にすればいける！！

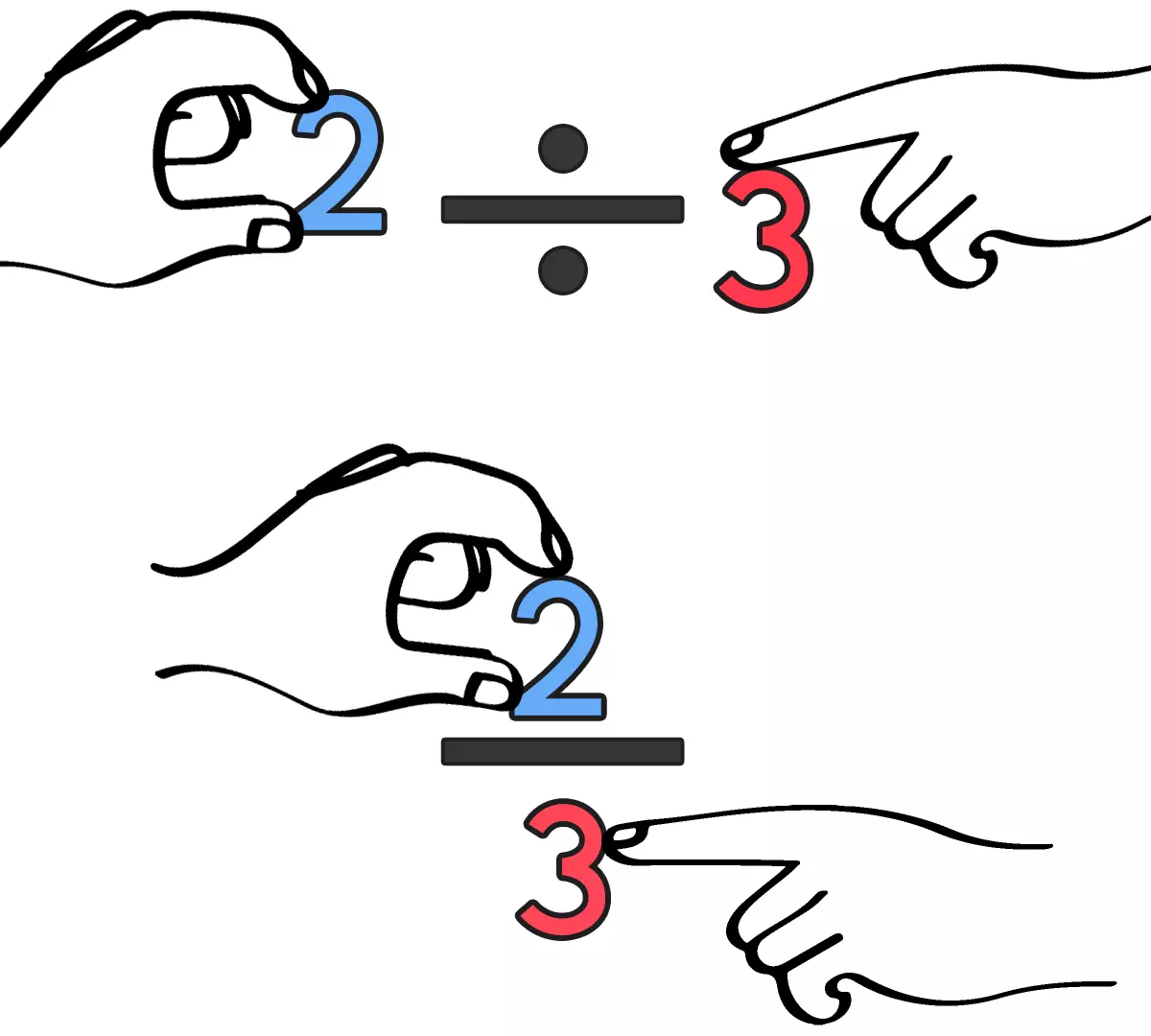
割り算を分数にする方法は割る数を分母に、割られる数を分子にする

2mのロープを3等分した 1つ分の長さは何m？？

$ 2 \div 3 = \dfrac{2}{3} $

答え $ \dfrac{2}{3} $m

分数は割り算にできるし

割り算は分数にできる

次の商を分数で表してね。ただし、仮分数は帯分数にすること

1÷3 ＝ $ \dfrac{1}{3} $
7÷9 ＝ $ \dfrac{7}{9} $
3÷7 ＝ $ \dfrac{3}{7} $
5÷6 ＝ $ \dfrac{5}{6} $
4÷9 ＝ $ \dfrac{4}{9} $
11÷6 ＝ $ 1\dfrac{5}{6} $
13÷7 ＝ $ 1\dfrac{6}{7} $
35÷17 ＝ $ 2\dfrac{1}{17} $

答えを分数で表しましょう。

1mのロープを3等分した 1つ分の長さは何m？？

(式と答え) 1÷3= $ \dfrac{1}{3} $ 答え $ \dfrac{1}{3}m $

9kgの米を7等分した 1つ分の重さは何kg？？

(式と答え) 9÷7= $ \dfrac{9}{7} $ 答え $ \dfrac{9}{7}kg $ または $ 1\dfrac{2}{7}kg $

4Lの水を9つの入れ物に等しく分けます。1つの入れ物に何L入っていますか？？

(式と答え) 4÷9= $ \dfrac{4}{9} $ 答え $ \dfrac{4}{9}L $

どっちの分数が大きいか

$ \dfrac{5}{7} $ と $ \dfrac{2}{3} $ の大きさを比べたくなってきた。

でもわからん

分母がちがうから分かりにくい。分母をそろえる「通分」をしよう。

$ \dfrac{5}{7} = \dfrac{5×3}{7×3}$ = $ \dfrac{15}{21} $

$ \dfrac{2}{3} = \dfrac{2×7}{3×7}$ = $ \dfrac{14}{21} $

$ \dfrac{5}{7} $ のほうが大きい

分数を小数にしても比べることができる。まぁやりやすいほうで

等号＝、不等号＞＜をつかって次の数をくらべよう。

等号(とうごう)・不等号(ふとうごう)の使い方

3 ＝ 3 (同じ)

3 ＞ 2 (3のほうが大きい)

3 ＜ 5 (5のほうが大きい)

$ \dfrac{3}{4} $ $ \frac{9}{12} \gt \frac{8}{12} $ $ \dfrac{2}{3} $
$ \dfrac{7}{12} $ $ \frac{35}{60} \lt \frac{36}{60} $ $ \dfrac{3}{5} $
$ \dfrac{11}{15} $ $ \frac{22}{30} \gt \frac{21}{30} $ $ \dfrac{7}{10} $
$ \dfrac{7}{9} $ $ \frac{28}{36} \lt \frac{30}{36} $ $ \dfrac{5}{6} $
$ \dfrac{11}{12} $ $ \frac{55}{60} \gt \frac{52}{60} $ $ \dfrac{13}{15} $
$ \dfrac{17}{14} $ $ \frac{34}{28} \lt \frac{35}{28} $ $ \dfrac{5}{4} $
$ \dfrac{5}{6} $ $ \frac{35}{42} \gt \frac{33}{42} $ $ \dfrac{11}{14} $
$ 1.1 $ $ = 1.1 $ $ 1\dfrac{1}{10} $
$ 1.5 $ $ \lt 1.8 $ $ \dfrac{9}{5} $
$ 0.72 $ $ \lt 0.75 $ $ \dfrac{3}{4} $

つぎの数を大きい順にならべてください。

$ \dfrac{5}{4} 1\dfrac{2}{5} 1\dfrac{3}{10} $

$ 1\dfrac{2}{5} 1\dfrac{3}{10} \dfrac{5}{4} $
通分して分母を20にするといい

$ \dfrac{4}{5} $ $ \dfrac{5}{6} $ $ 0.7 $ $ \dfrac{2}{3} $ $ \dfrac{11}{15} $

$ \dfrac{5}{6} $ $ \dfrac{4}{5} $ $ \dfrac{11}{15} $ $ 0.7 $ $ \dfrac{2}{3} $
0.7を$ \dfrac{7}{10} $に。あとは通分して分母を30にする

5年生 ｢分数｣ 第1弾！約分も通分もこれで完璧だ

同じ大きさの分数

約分してスッキリ！

通分のやり方

通分 これどうする？

小数を分数にする方法分数を小数にする方法

小数を分数にする方法

分数を小数にする方法

割りきれない割り算も分数ならバシッと

そんな割りきれない割り算も！？答えを分数にすればいける！！

どっちの分数が大きいか

等号 ＝ 、 不等号＞ ＜ をつかって 次の数をくらべよう。

つぎの数を大きい順にならべてください。

5年生｢分数｣第1弾！
約分も通分もこれで完璧だ

通分これどうする？

小数を分数にする方法
分数を小数にする方法

そんな割りきれない割り算も！？
答えを分数にすればいける！！

等号＝、不等号＞＜をつかって次の数をくらべよう。